Giải Bài Tập 1.11 Trang 14 Toán 12 Tập 1

Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

Bài tập 1.11 trang 14 SGK Toán 12 tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số và đạo hàm để giải quyết các bài toán thực tế.

tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.11 trang 14, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

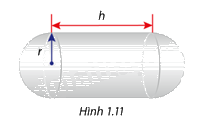
Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0)và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 ({m^3}). Để sơn mắt ngoài phần hình cầu cần 20 000cho 1 ({m^2}) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 ({m^2}).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không đư

Đề bài

Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét (h > 0) và 2 đầu là các nửa hình cầu bán kính r (r > 0) (Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000 cho 1 \({m^2}\), còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\). Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa (bao gồm diện tích xung quanh hình trụ và diện tích 2 nửa hình cầu) là nhỏ nhất, biết rằng bán kính r không được vượt quá 50m.

Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá 2

Bước 1: Lập công thức tính chi phí sơn.

Bước 2: Lập bảng biến thiên của hàm số.

Bước 3: Tính chi phí nhỏ nhất để sơn là tìm giá trị nhỏ nhất của hàm số.

Lời giải chi tiết

Ta có thể tích thùng nhiên liệu là:

\(V = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow 144000\pi = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow h = \frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}\).

DIện tích xung quanh thùng nhiên liệu là là: \(S = 4{r^2}\pi + 2rh\pi \).

Số tiền cần để sơn xung quanh thùng nhiên liệu là:

\(T = 20000.4{r^2}\pi + 10000.2rh\pi = 80000{r^2}\pi + 20000rh\pi \left( {\frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}} \right)\)

\( = 80000{r^2}\pi + 2880000000\frac{\pi }{r} - \frac{{80000}}{3}{r^2}\pi = \frac{{160000}}{3}{r^2}\pi + 2880000000\frac{\pi }{r}\).

Bài toán trở thành tìm r để để hàm số T nhỏ nhất.

Ta có:

\(T' = \frac{{160000}}{3}\left( {2r} \right)\pi - 2880000000\frac{\pi }{{{r^2}}} = 0 \Leftrightarrow {r^3} = 27000 \Leftrightarrow r = 30\).

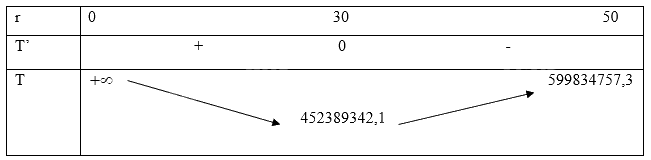
Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá 3

Vậy để chi phí sơn là nhỏ nhất thì r = 30.

Giải Bài Tập 1.11 Trang 14 SGK Toán 12 Tập 1: Phương Pháp Giải Chi Tiết

Bài tập 1.11 trang 14 SGK Toán 12 tập 1 thuộc chương trình học về hàm số và đạo hàm. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản sau:

Khái niệm hàm số: Hàm số là một quy tắc tương ứng giữa mỗi giá trị của biến độc lập (x) với một giá trị duy nhất của biến phụ thuộc (y).
Đạo hàm: Đạo hàm của hàm số tại một điểm là tốc độ thay đổi tức thời của hàm số tại điểm đó.
Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
Ứng dụng của đạo hàm: Nghiên cứu hàm số, tìm cực trị, giải phương trình, bất phương trình.

Nội Dung Bài Tập 1.11 Trang 14

Bài tập 1.11 thường yêu cầu học sinh thực hiện các thao tác sau:

Xác định tập xác định của hàm số.
Tính đạo hàm của hàm số.
Tìm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Vẽ đồ thị hàm số.

Lời Giải Chi Tiết Bài Tập 1.11 Trang 14

(Giả sử bài tập 1.11 là: Cho hàm số y = x³ - 3x² + 2. Tìm cực đại, cực tiểu của hàm số.)

Bước 1: Tính đạo hàm cấp một của hàm số:

y' = 3x² - 6x

Bước 2: Tìm các điểm dừng của hàm số:

y' = 0 ⇔ 3x² - 6x = 0 ⇔ 3x(x - 2) = 0

Vậy, các điểm dừng của hàm số là x = 0 và x = 2.

Bước 3: Xét dấu đạo hàm cấp một để xác định cực trị:

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

Từ bảng xét dấu, ta thấy:

Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Mẹo Giải Bài Tập Nhanh

Để giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 nhanh chóng và chính xác, bạn nên:

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính bỏ túi để tính toán nhanh chóng.
Kiểm tra lại kết quả sau khi giải xong.

Tổng Kết

Bài tập 1.11 trang 14 SGK Toán 12 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải nhanh mà tusach.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.

Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá