Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 17, 18 SGK Toán 12 tập 1. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.

tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.

Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17. a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\) b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Cùng khám phá

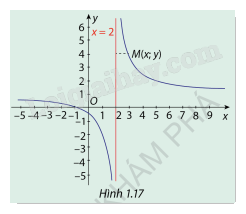
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.

a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\)

b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá 0 1

Phương pháp giải:

a) Nhìn đồ thị hàm số rồi nhận xét

b) Phân tích, rồi tính \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

Lời giải chi tiết:

a) Dựa vào đồ thị hàm số ta thấy:

Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ

b) Ta có \(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = + \infty \;\;\)

\(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = - \infty \;\;\)

LT2

Trả lời câu hỏi Luyện tập 2 trang 18 SGK Toán 12 Cùng khám phá

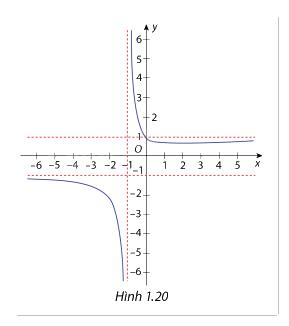
Cho hàm số \(y = f(x) = \frac{{\sqrt {{x^2} + 1} }}{{x + 1}}\) có đồ thị là đường cong như hình 1.20. Hãy xác nhận các đường tiệm cận đứng và đường tiệm cận ngang của hàm số đã cho.

Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá 1 1

Phương pháp giải:

Xét \(f(x).\)

Lời giải chi tiết:

Ta có \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = - \infty \;\), \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\;\)=\(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = + \infty \;\)

Suy ra x = - 1 là đường tiệm cận đứng của hàm số.

Ta có \(\mathop {\lim }\limits_{x \to + \infty } f(x)\; = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\), \(\mathop {\lim }\limits_{x \to - \infty } f(x)\; = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{1}{x}}} = 1\;\;\)

Suy ra y = 1 là đường tiệm cận ngang của hàm số.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ2
LT2

Trả lời câu hỏi Hoạt động 2 trang 17 SGK Toán 12 Cùng khám phá

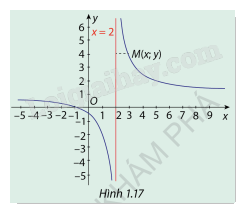
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.

a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\)

b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải:

a) Nhìn đồ thị hàm số rồi nhận xét

b) Phân tích, rồi tính \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

Lời giải chi tiết:

a) Dựa vào đồ thị hàm số ta thấy:

Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ

b) Ta có \(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = + \infty \;\;\)

\(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = - \infty \;\;\)

Trả lời câu hỏi Luyện tập 2 trang 18 SGK Toán 12 Cùng khám phá

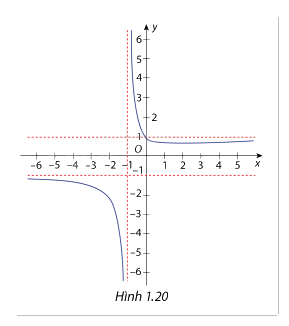
Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá 2

Phương pháp giải:

Xét \(f(x).\)

Lời giải chi tiết:

Suy ra x = - 1 là đường tiệm cận đứng của hàm số.

Suy ra y = 1 là đường tiệm cận ngang của hàm số.

Giải mục 2 trang 17, 18 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải

Mục 2 trang 17, 18 SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 12.

Nội dung chi tiết Mục 2 trang 17, 18 SGK Toán 12 tập 1

Mục 2 thường bao gồm các nội dung sau:

Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, đạo hàm của hàm hợp.
Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm số mũ, hàm số logarit, hàm số lượng giác.
Ứng dụng của đạo hàm: Sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số, giải các bài toán liên quan đến tối ưu hóa.

Hướng dẫn giải các bài tập tiêu biểu

Bài 1: Tính đạo hàm của hàm số f(x) = x² + 3x - 2

Lời giải:

f'(x) = 2x + 3

Bài 2: Tìm cực trị của hàm số y = x³ - 3x² + 2

Lời giải:

Tính đạo hàm y' = 3x² - 6x
Giải phương trình y' = 0 để tìm các điểm cực trị: 3x² - 6x = 0 => x = 0 hoặc x = 2
Lập bảng biến thiên để xác định cực đại, cực tiểu:

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

Vậy hàm số đạt cực đại tại x = 0, y = 2 và đạt cực tiểu tại x = 2, y = -2.

Mẹo giải nhanh và hiệu quả

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
Tham khảo các tài liệu tham khảo, bài giảng trên mạng để hiểu sâu hơn về kiến thức.

Tài liệu tham khảo hữu ích

Ngoài SGK Toán 12 tập 1, các em có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 12
Các trang web học Toán trực tuyến như tusach.vn, VietJack, Hoc24...
Các video bài giảng trên YouTube

Kết luận

Hy vọng với những hướng dẫn chi tiết và lời giải bài tập trong bài viết này, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến đạo hàm. Chúc các em học tốt và đạt kết quả cao trong môn Toán 12!

Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá