Giải trang 96, 97, 98, 99, 100, 101 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Toán 12 Tập 1 Trang 96-101
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác nhất cho các bài tập Toán 12 tập 1 trang 96, 97, 98, 99, 100, 101. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những lời giải chất lượng, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Bảng 3.13 là mẫu số liệu ghép nhóm về lương của 40 nhân viên công ty M mà anh Bình có:
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 96 SGK Toán 12 Cùng khám phá
Bảng 3.13 là mẫu số liệu ghép nhóm về lương của 40 nhân viên công ty M mà anh Bình có:
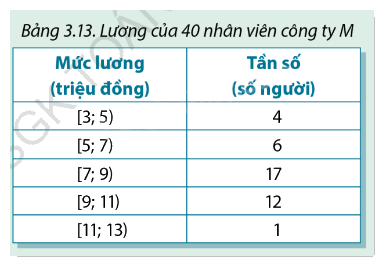
a) Hãy ước tính lương trung bình \({\overline X _M}\) của 40 nhân viên.
b) Điều anh Bình quan tâm là độ lệch trung bình giữa lương của mỗi nhân viên so với lương trung bình \({\overline X _M}\). Anh Bình có thể ước lượng độ lệch giữa lương của những nhân viên thuộc nhóm thứ nhất (nhóm lương từ 3 đến dưới 5 triệu đồng) so với số trung bình qua giá trị nào?
c) Dựa vào công thức tính trung bình của mẫu số liệu ghép nhóm và hai công thức tính phương sai, độ lệch chuẩn của mẫu số liệu không ghép nhóm, hãy đề xuất một cách ước tính phương sai và độ lệch chuẩn của mẫu số liệu gốc mà anh Bình không có (bảng lương của từng người).
Phương pháp giải:
a) Công thức tính điểm trung bình
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\), trong đó:
- \({x_i}\) là giá trị đại diện của khoảng lương thứ \(i\).
- \({n_i}\) là tần số của khoảng lương thứ \(i\).
- \(N\) là tổng số nhân viên.
b) Sử dụng giá trị trung bình của nhóm lương từ 3 đến dưới 5 triệu đồng.
Công thức:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right|\)
c)
- Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
a) Tính lương trung bình \({\overline X _M}\):
\(\begin{array}{l}[3;5):\frac{{3 + 5}}{2} = 4;\\(5;7):\frac{{5 + 7}}{2} = 6{\rm{ }};\\(7;9):\frac{{7 + 9}}{2} = 8{\rm{ }};\\(9;11)\frac{{9 + 11}}{2} = 10{\rm{ }};\\(11;13)\frac{{11 + 13}}{2} = 12{\rm{ }}\end{array}\)
Lương trung bình:
\({\overline X _M} = \frac{{\sum {{x_i}.{n_i}} }}{N} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
b) Ước lượng độ lệch trung bình:
Giá trị đại diện của nhóm thứ nhất (3 đến 5 triệu đồng): 4 triệu đồng
Độ lệch giữa lương của nhóm này và lương trung bình là:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right| = \left| {4 - 8} \right| = 4\) triệu đồng
c)
Công thức tính trung bình là
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
Ta biết rằng các giá trị \({x_i}\) nằm trong các nhóm, và mỗi nhóm có trung điểm \({x_j}\) và tần số \({n_j}\). Do đó, ta có thể viết lại tổng trên bằng cách thay thế từng \({x_i}\) trong mỗi nhóm bằng trung điểm \({x_j}\):
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2} = \frac{1}{N}\sum\limits_{j = 1}^k {\sum\limits_{i = 1}^{{n_j}} {{{({x_i} - \overline x )}^2}} } = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Vậy công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Và độ lệch chuẩn của mẫu số liệu ghép nhóm vẫn là:
\(S = \sqrt {{S^2}} \).
VD1
Trả lời câu hỏi Vận dụng 1 trang 101 SGK Toán 12 Cùng khám phá
Bộ phận kiểm tra chất lượng sản phẩm dùng máy để đo (chính xác đến 0,001 mm) độ dày của một chi tiết máy. Kết quả đo một số sản phẩm được thống kê trong bảng sau:

a) Tính phương sai và độ lệch chuẩn của độ dày chi tiết máy.
b) Giải thích tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này.
Phương pháp giải:
a)
- Công thức tính phương sai:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
b) Độ lệch chuẩn càng nhỏ chứng tỏ các giá trị đo được càng gần với giá trị trung bình, nghĩa là độ chính xác của máy đo cao hơn. Trong trường hợp này, độ dày chi tiết máy càng đồng nhất thì chất lượng sản phẩm càng cao.
Lời giải chi tiết:
a)
Kích thước của mẫu số liệu là: \(N = 3 + 7 + 23 + 25 + 2 = 60\)
Độ dày trung bình:
\(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{18,5.3 + 19,5.7 + 20,5.23 + 21,5.25 + 22,5.2}}{{60}} = 20,77\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{{3.{{(18,5 - 20,77)}^2} + 7.{{(19,5 - 20,77)}^2} + 23.{{(20,5 - 20,77)}^2} + 25.{{(21,5 - 20,77)}^2} + 2.{{(22,5 - 20,77)}^2}}}{{60}}\\{S^2} \approx 0,79557\end{array}\).
Độ lệch chuẩn là:
\(S = \sqrt {0,79557} \approx 0,89195\)
Tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này chính là: Độ lệch chuẩn nhỏ chứng tỏ các giá trị đo độ dày của chi tiết máy không bị phân tán nhiều, đảm bảo tính đồng nhất và chất lượng sản phẩm.
LT2
Trả lời câu hỏi Luyện tập 2 trang 101 SGK Toán 12 Cùng khám phá
Số tiền ghi trên hoá đơn của 150 khách hàng lấy ngẫu nhiên trong một ngày được siêu thị ghi lại ở bảng dưới đây:

Tìm phương sai, độ lệch chuẩn của mẫu số liệu về số tiền ghi trên hoá đơn.
Phương pháp giải:
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
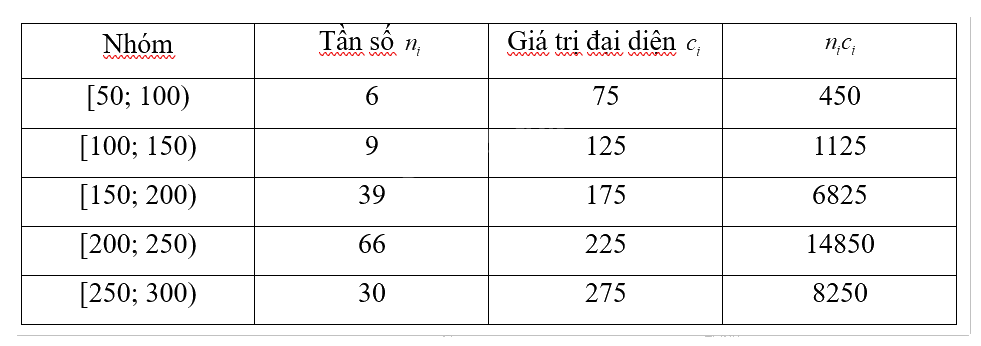
Vì có 5 nhóm nên k = 5. Số tiền trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{450 + 1125 + 6825 + 14850 + 8250}}{{150}} = 210\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2}\\{S^2} = \frac{{6.{{(75 - 210)}^2} + 9.{{(125 - 210)}^2} + 39.{{(175 - 210)}^2} + 66.{{(225 - 210)}^2} + 30.{{(275 - 210)}^2}}}{{150}} = 2425\end{array}\)
Độ lệch chuẩn là:
\(S = \sqrt {2425} \approx 49,24\)
LT1
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Bảng dưới đây tổng hợp thời gian hoàn thành bài kiểm tra IQ của 50 học sinh lớp 9:

Tính trung bình và độ lệch chuẩn của mẫu số liệu đã cho. Nêu ý nghĩa của kết quả tìm được.
Phương pháp giải:
Áp dụng các công thức tính trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm:
- Công thức tính trung bình là
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{c_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
Kích thước của mẫu số liệu là N = 50.
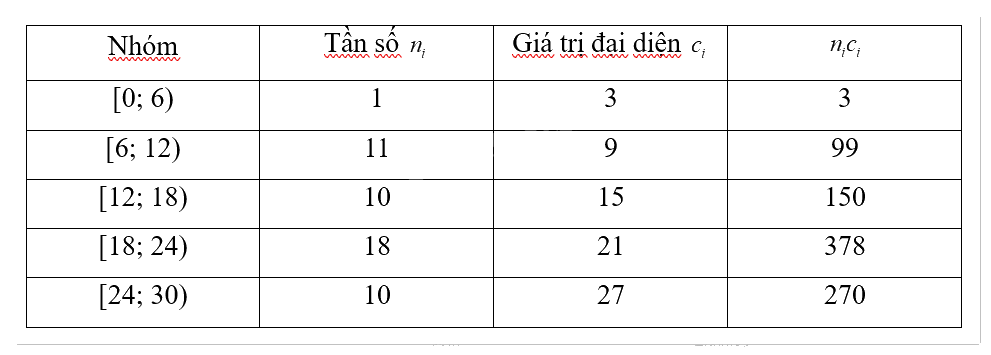
Vì có 5 nhóm nên k = 5. Trung bình mẫu:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{3 + 99 + 150 + 378 + 270}}{{50}} = 18\)
Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2} = \frac{{1.{{(3 - 18)}^2} + 11.{{(9 - 18)}^2} + 10.{{(15 - 18)}^2} + 18.{{(21 - 18)}^2} + 10.{{(27 - 18)}^2}}}{{50}} = \frac{{1089}}{{25}} = 43,56\)
Độ lệch chuẩn là:
\(S = \sqrt {{S^2}} = \sqrt {43,56} = 6,6\) Các kết quả vừa tìm được cho thấy thời gian làm bài kiểm tra IQ của các học sinh lớp 9 có sự chênh lệch khoảng 6,6 so với thời gian trung bình.
VD2
Trả lời câu hỏi Vận dụng 2 trang 101 SGK Toán 12 Cùng khám phá
Trở lại với vấn đề của anh Bình.
Ta đã biết bảng 3.13 là số liệu anh Bình có về lương của 40 nhân viên có tuổi nghề dưới 5 năm thuộc công ty M. Để tiện tính toán, ta chép lại dưới đây bảng 3.13. Đối với công ty N, anh Bình cũng thu thập được một số mẫu số liệu ghép nhóm về lương của 42 nhân viên có tuổi nghề dưới 5 năm (Bảng 3.20).
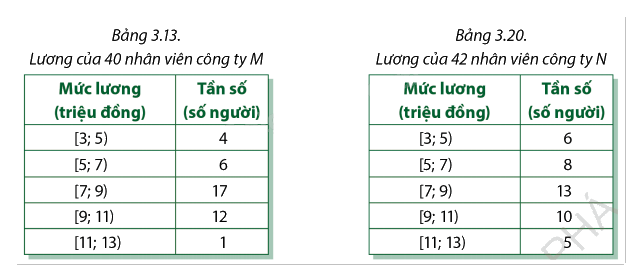
Nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm chênh lệch nhau ít hơn thì anh Bình nên chọn công ty M hay N?
Phương pháp giải:
- Tính mức lương trung bình của từng nhóm nhân viên theo công thức:
\(\overline L = \frac{{\sum {{f_i}.{L_i}} }}{{\sum {{f_i}} }}\)
Trong đó \({f_i}\) là số lượng nhân viên trong nhóm với mức lương \({L_i}\).
- Tìm độ lệch chuẩn của mức lương trong từng công ty và so sánh.
\(S = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - \overline L } \right)} }}{{\sum {{f_i}} }}} \)
Lời giải chi tiết:
Mức lương trung bình của hai công ty là:
\({\overline L _M} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_M}}} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
\({\overline L _N} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_N}}} = \frac{{4.6 + 6.8 + 8.13 + 10.10 + 12.5}}{{42}} = 8\)
Độ lệch chuẩn mức lương của hai công ty là:
\({S_M} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_M}} \right)} }}{{{f_M}}}} = \sqrt {\frac{{4.{{(4 - 8)}^2} + 6.{{(6 - 8)}^2} + 17.{{(8 - 8)}^2} + 12.{{(10 - 8)}^2} + 1.{{(12 - 8)}^2}}}{{40}}} \approx 1,95\)
\({S_N} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_N}} \right)} }}{{{f_N}}}} = \sqrt {\frac{{6.{{(4 - 8)}^2} + 8.{{(6 - 8)}^2} + 13.{{(8 - 8)}^2} + 10.{{(10 - 8)}^2} + 5.{{(12 - 8)}^2}}}{{42}}} \approx 2,43\)
Nhận thấy độ lệch so với mức lương của công ty N cao hơn công ty M.
Như vậy, nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm thì nên chọn công ty M.
- HĐ1
- LT1
- LT2
- VD1
- VD2
Trả lời câu hỏi Hoạt động 1 trang 96 SGK Toán 12 Cùng khám phá
Bảng 3.13 là mẫu số liệu ghép nhóm về lương của 40 nhân viên công ty M mà anh Bình có:
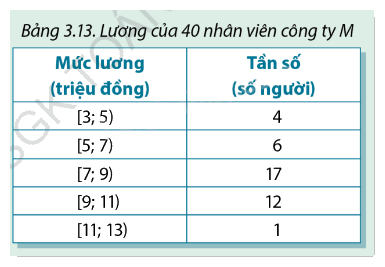
a) Hãy ước tính lương trung bình \({\overline X _M}\) của 40 nhân viên.
b) Điều anh Bình quan tâm là độ lệch trung bình giữa lương của mỗi nhân viên so với lương trung bình \({\overline X _M}\). Anh Bình có thể ước lượng độ lệch giữa lương của những nhân viên thuộc nhóm thứ nhất (nhóm lương từ 3 đến dưới 5 triệu đồng) so với số trung bình qua giá trị nào?
c) Dựa vào công thức tính trung bình của mẫu số liệu ghép nhóm và hai công thức tính phương sai, độ lệch chuẩn của mẫu số liệu không ghép nhóm, hãy đề xuất một cách ước tính phương sai và độ lệch chuẩn của mẫu số liệu gốc mà anh Bình không có (bảng lương của từng người).
Phương pháp giải:
a) Công thức tính điểm trung bình
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\), trong đó:
- \({x_i}\) là giá trị đại diện của khoảng lương thứ \(i\).
- \({n_i}\) là tần số của khoảng lương thứ \(i\).
- \(N\) là tổng số nhân viên.
b) Sử dụng giá trị trung bình của nhóm lương từ 3 đến dưới 5 triệu đồng.
Công thức:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right|\)
c)
- Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
a) Tính lương trung bình \({\overline X _M}\):
\(\begin{array}{l}[3;5):\frac{{3 + 5}}{2} = 4;\\(5;7):\frac{{5 + 7}}{2} = 6{\rm{ }};\\(7;9):\frac{{7 + 9}}{2} = 8{\rm{ }};\\(9;11)\frac{{9 + 11}}{2} = 10{\rm{ }};\\(11;13)\frac{{11 + 13}}{2} = 12{\rm{ }}\end{array}\)
Lương trung bình:
\({\overline X _M} = \frac{{\sum {{x_i}.{n_i}} }}{N} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
b) Ước lượng độ lệch trung bình:
Giá trị đại diện của nhóm thứ nhất (3 đến 5 triệu đồng): 4 triệu đồng
Độ lệch giữa lương của nhóm này và lương trung bình là:
\(\Delta = \left| {{x_{[3;5)}} - {{\overline X }_M}} \right| = \left| {4 - 8} \right| = 4\) triệu đồng
c)
Công thức tính trung bình là
\({\bar X_M} = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
Công thức tính phương sai của mẫu số liệu không ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2}\)
Ta biết rằng các giá trị \({x_i}\) nằm trong các nhóm, và mỗi nhóm có trung điểm \({x_j}\) và tần số \({n_j}\). Do đó, ta có thể viết lại tổng trên bằng cách thay thế từng \({x_i}\) trong mỗi nhóm bằng trung điểm \({x_j}\):
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i}} - \overline x {)^2} = \frac{1}{N}\sum\limits_{j = 1}^k {\sum\limits_{i = 1}^{{n_j}} {{{({x_i} - \overline x )}^2}} } = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Vậy công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{j = 1}^k {{n_j}({x_j}} - \overline x {)^2}\)
Và độ lệch chuẩn của mẫu số liệu ghép nhóm vẫn là:
\(S = \sqrt {{S^2}} \).
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Bảng dưới đây tổng hợp thời gian hoàn thành bài kiểm tra IQ của 50 học sinh lớp 9:

Tính trung bình và độ lệch chuẩn của mẫu số liệu đã cho. Nêu ý nghĩa của kết quả tìm được.
Phương pháp giải:
Áp dụng các công thức tính trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm:
- Công thức tính trung bình là
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{c_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
Kích thước của mẫu số liệu là N = 50.
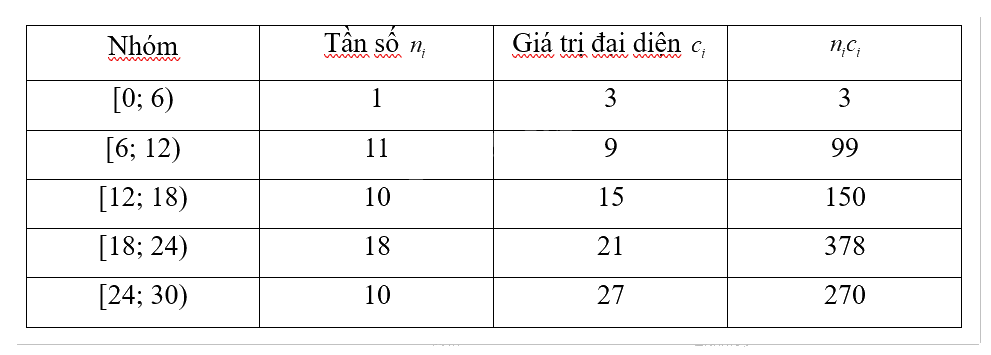
Vì có 5 nhóm nên k = 5. Trung bình mẫu:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{3 + 99 + 150 + 378 + 270}}{{50}} = 18\)
Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2} = \frac{{1.{{(3 - 18)}^2} + 11.{{(9 - 18)}^2} + 10.{{(15 - 18)}^2} + 18.{{(21 - 18)}^2} + 10.{{(27 - 18)}^2}}}{{50}} = \frac{{1089}}{{25}} = 43,56\)
Độ lệch chuẩn là:
\(S = \sqrt {{S^2}} = \sqrt {43,56} = 6,6\) Các kết quả vừa tìm được cho thấy thời gian làm bài kiểm tra IQ của các học sinh lớp 9 có sự chênh lệch khoảng 6,6 so với thời gian trung bình.
Trả lời câu hỏi Luyện tập 2 trang 101 SGK Toán 12 Cùng khám phá
Số tiền ghi trên hoá đơn của 150 khách hàng lấy ngẫu nhiên trong một ngày được siêu thị ghi lại ở bảng dưới đây:

Tìm phương sai, độ lệch chuẩn của mẫu số liệu về số tiền ghi trên hoá đơn.
Phương pháp giải:
- Công thức tính phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
Lời giải chi tiết:
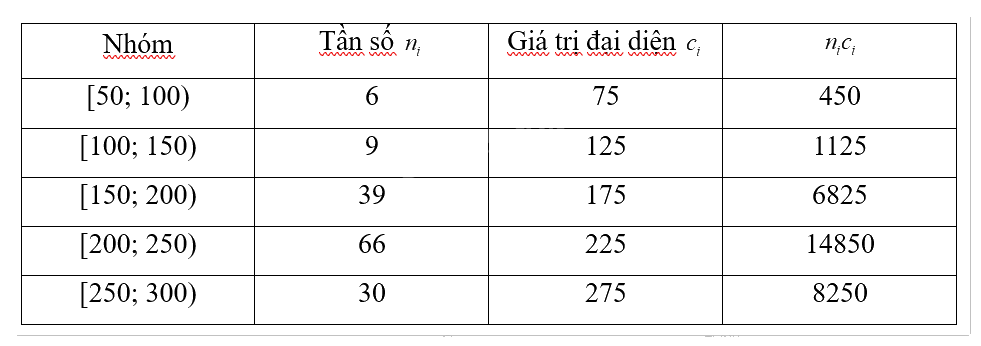
Vì có 5 nhóm nên k = 5. Số tiền trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^5 {\left( {{c_i}{n_i}} \right)} }}{N} = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{450 + 1125 + 6825 + 14850 + 8250}}{{150}} = 210\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{1}{N}\sum\limits_{i = 1}^5 {{n_i}({c_i}} - \bar x{)^2}\\{S^2} = \frac{{6.{{(75 - 210)}^2} + 9.{{(125 - 210)}^2} + 39.{{(175 - 210)}^2} + 66.{{(225 - 210)}^2} + 30.{{(275 - 210)}^2}}}{{150}} = 2425\end{array}\)
Độ lệch chuẩn là:
\(S = \sqrt {2425} \approx 49,24\)
Trả lời câu hỏi Vận dụng 1 trang 101 SGK Toán 12 Cùng khám phá
Bộ phận kiểm tra chất lượng sản phẩm dùng máy để đo (chính xác đến 0,001 mm) độ dày của một chi tiết máy. Kết quả đo một số sản phẩm được thống kê trong bảng sau:

a) Tính phương sai và độ lệch chuẩn của độ dày chi tiết máy.
b) Giải thích tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này.
Phương pháp giải:
a)
- Công thức tính phương sai:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
b) Độ lệch chuẩn càng nhỏ chứng tỏ các giá trị đo được càng gần với giá trị trung bình, nghĩa là độ chính xác của máy đo cao hơn. Trong trường hợp này, độ dày chi tiết máy càng đồng nhất thì chất lượng sản phẩm càng cao.
Lời giải chi tiết:
a)
Kích thước của mẫu số liệu là: \(N = 3 + 7 + 23 + 25 + 2 = 60\)
Độ dày trung bình:
\(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2} + {c_3}{n_3} + {c_4}{n_4} + {c_5}{n_5}}}{N} = \frac{{18,5.3 + 19,5.7 + 20,5.23 + 21,5.25 + 22,5.2}}{{60}} = 20,77\)
Phương sai của mẫu số liệu:
\(\begin{array}{l}{S^2} = \frac{{3.{{(18,5 - 20,77)}^2} + 7.{{(19,5 - 20,77)}^2} + 23.{{(20,5 - 20,77)}^2} + 25.{{(21,5 - 20,77)}^2} + 2.{{(22,5 - 20,77)}^2}}}{{60}}\\{S^2} \approx 0,79557\end{array}\).
Độ lệch chuẩn là:
\(S = \sqrt {0,79557} \approx 0,89195\)
Tầm quan trọng của việc có độ lệch chuẩn nhỏ trong trường hợp này chính là: Độ lệch chuẩn nhỏ chứng tỏ các giá trị đo độ dày của chi tiết máy không bị phân tán nhiều, đảm bảo tính đồng nhất và chất lượng sản phẩm.
Trả lời câu hỏi Vận dụng 2 trang 101 SGK Toán 12 Cùng khám phá
Trở lại với vấn đề của anh Bình.
Ta đã biết bảng 3.13 là số liệu anh Bình có về lương của 40 nhân viên có tuổi nghề dưới 5 năm thuộc công ty M. Để tiện tính toán, ta chép lại dưới đây bảng 3.13. Đối với công ty N, anh Bình cũng thu thập được một số mẫu số liệu ghép nhóm về lương của 42 nhân viên có tuổi nghề dưới 5 năm (Bảng 3.20).
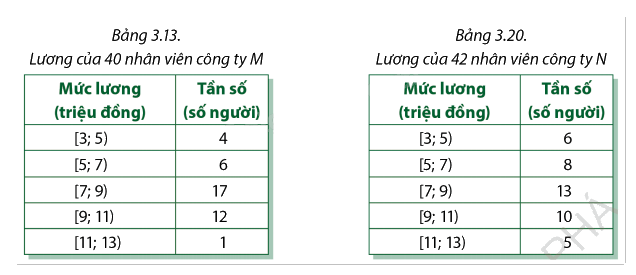
Nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm chênh lệch nhau ít hơn thì anh Bình nên chọn công ty M hay N?
Phương pháp giải:
- Tính mức lương trung bình của từng nhóm nhân viên theo công thức:
\(\overline L = \frac{{\sum {{f_i}.{L_i}} }}{{\sum {{f_i}} }}\)
Trong đó \({f_i}\) là số lượng nhân viên trong nhóm với mức lương \({L_i}\).
- Tìm độ lệch chuẩn của mức lương trong từng công ty và so sánh.
\(S = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - \overline L } \right)} }}{{\sum {{f_i}} }}} \)
Lời giải chi tiết:
Mức lương trung bình của hai công ty là:
\({\overline L _M} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_M}}} = \frac{{4.4 + 6.6 + 8.17 + 10.12 + 12.1}}{{40}} = 8\)
\({\overline L _N} = \frac{{\sum {{f_i}} .{L_i}}}{{{f_N}}} = \frac{{4.6 + 6.8 + 8.13 + 10.10 + 12.5}}{{42}} = 8\)
Độ lệch chuẩn mức lương của hai công ty là:
\({S_M} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_M}} \right)} }}{{{f_M}}}} = \sqrt {\frac{{4.{{(4 - 8)}^2} + 6.{{(6 - 8)}^2} + 17.{{(8 - 8)}^2} + 12.{{(10 - 8)}^2} + 1.{{(12 - 8)}^2}}}{{40}}} \approx 1,95\)
\({S_N} = \sqrt {\frac{{\sum {{f_i}.\left( {{L_i} - {{\bar L}_N}} \right)} }}{{{f_N}}}} = \sqrt {\frac{{6.{{(4 - 8)}^2} + 8.{{(6 - 8)}^2} + 13.{{(8 - 8)}^2} + 10.{{(10 - 8)}^2} + 5.{{(12 - 8)}^2}}}{{42}}} \approx 2,43\)
Nhận thấy độ lệch so với mức lương của công ty N cao hơn công ty M.
Như vậy, nếu muốn làm việc ở nơi mà lương giữa các nhân viên có tuổi nghề dưới 5 năm thì nên chọn công ty M.
Giải Toán 12 Tập 1 Trang 96-101: Hướng Dẫn Chi Tiết và Dễ Hiểu
Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 trang 96, 97, 98, 99, 100, 101 của tusach.vn. Ở phần này, chúng ta sẽ cùng nhau đi sâu vào giải quyết các bài tập thuộc chương trình học Toán 12 tập 1, tập trung vào các chủ đề quan trọng như đạo hàm, giới hạn, và các ứng dụng của đạo hàm.
Nội Dung Chính Của Trang 96-101 Toán 12 Tập 1
Trang 96-101 SGK Toán 12 tập 1 thường chứa các bài tập liên quan đến:
- Đạo hàm của hàm số lượng giác: Các bài tập này yêu cầu các em nắm vững công thức đạo hàm của sinx, cosx, tanx, cotx và áp dụng chúng để tính đạo hàm của các hàm số phức tạp hơn.
- Quy tắc tính đạo hàm: Ôn lại và vận dụng các quy tắc như quy tắc tích, quy tắc thương, quy tắc hàm hợp để giải quyết các bài toán đạo hàm.
- Ứng dụng của đạo hàm: Tìm cực trị của hàm số, khảo sát hàm số, và giải các bài toán liên quan đến tối ưu hóa.
Hướng Dẫn Giải Chi Tiết Từng Bài Tập
Chúng tôi sẽ cung cấp lời giải chi tiết cho từng bài tập, bao gồm:
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài và các thông tin đã cho.
- Lựa chọn phương pháp giải: Chọn phương pháp phù hợp nhất để giải quyết bài toán.
- Thực hiện các bước giải: Trình bày các bước giải một cách rõ ràng, logic và dễ hiểu.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả cuối cùng là chính xác và phù hợp với yêu cầu của đề bài.
Ví dụ Giải Bài Tập (Trang 96)
Bài 1: Tính đạo hàm của hàm số y = sin(2x + 1).
Lời giải:
Sử dụng quy tắc hàm hợp, ta có:
y' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Lưu Ý Khi Giải Bài Tập Toán 12
Để đạt kết quả tốt nhất khi giải bài tập Toán 12, các em cần:
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định nghĩa, định lý, công thức và quy tắc.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo sách giáo khoa, sách bài tập, và các nguồn tài liệu trực tuyến uy tín.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Tại Sao Nên Chọn tusach.vn Để Giải Toán 12?
tusach.vn tự hào là một trong những trang web hàng đầu cung cấp lời giải bài tập Toán 12 tập 1 chính xác, chi tiết và dễ hiểu. Chúng tôi cam kết:
- Lời giải được kiểm duyệt bởi các giáo viên giàu kinh nghiệm.
- Giao diện thân thiện, dễ sử dụng.
- Cập nhật lời giải nhanh chóng.
- Miễn phí truy cập.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và cùng chúng tôi chinh phục môn Toán 12!
| Chương | Nội Dung |
|---|---|
| 1 | Đạo hàm |
| 2 | Giới hạn |
| 3 | Ứng dụng của đạo hàm |