Giải Bài Tập 2.3 Trang 64 SGK Toán 12 Tập 1

Giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.3 trang 64 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp kiến thức chính xác và dễ hiểu nhất.

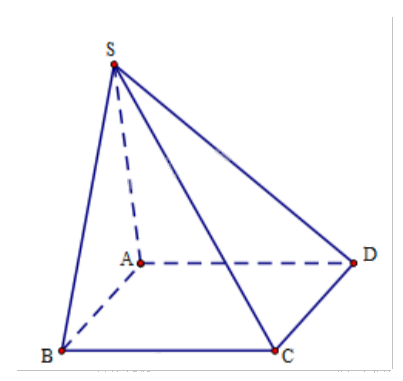
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng:

\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)

Phương pháp giải - Xem chi tiết Giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 - Cùng khám phá 1

Sử dụng tính chất của hình bình hành và phép biến đổi vectơ.

Lời giải chi tiết

Giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 - Cùng khám phá 2

Ta có thể viết:

\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} + \overrightarrow {BA} ) + (\overrightarrow {SD} + \overrightarrow {DC} )\)

Thay \(\overrightarrow {BA} = - \overrightarrow {AB} \) và \(\overrightarrow {DC} = - \overrightarrow {CD} \) vào biểu thức trên, ta được:

\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} - \overrightarrow {AB} ) + (\overrightarrow {SD} - \overrightarrow {CD} )\)

Sử dụng tính chất của hình bình hành:

\(\overrightarrow {AB} = \overrightarrow {DC} \quad {\rm{và}}\quad \overrightarrow {AD} = \overrightarrow {BC} \)

Nên ta có:

\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} - \overrightarrow {AB} + \overrightarrow {SD} + \overrightarrow {DC} = \overrightarrow {SB} + \overrightarrow {SD} \)

Vậy đẳng thức \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) đã được chứng minh.

Giải Bài Tập 2.3 Trang 64 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 2.3 trang 64 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

I. Đề Bài Bài Tập 2.3 Trang 64 SGK Toán 12 Tập 1

(Đề bài cụ thể của bài tập 2.3 sẽ được chèn vào đây. Ví dụ: Khảo sát hàm số y = x³ - 3x² + 2)

II. Phương Pháp Giải

Bước 1: Xác định tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
Bước 2: Tính đạo hàm cấp nhất y'. Đạo hàm cấp nhất giúp chúng ta xác định các điểm nghi ngờ là cực trị.
Bước 3: Tìm các điểm cực trị. Giải phương trình y' = 0 để tìm các điểm nghi ngờ là cực trị. Sau đó, kiểm tra dấu của y' để xác định loại cực trị (cực đại hoặc cực tiểu).
Bước 4: Lập bảng biến thiên. Bảng biến thiên giúp chúng ta hình dung được sự biến đổi của hàm số trên các khoảng xác định.
Bước 5: Kết luận về tính đơn điệu và cực trị của hàm số. Dựa vào bảng biến thiên, chúng ta có thể kết luận về khoảng đồng biến, nghịch biến và các điểm cực trị của hàm số.

III. Lời Giải Chi Tiết Bài Tập 2.3 Trang 64 SGK Toán 12 Tập 1

(Lời giải chi tiết của bài tập 2.3 sẽ được trình bày ở đây, bao gồm các bước giải cụ thể và giải thích rõ ràng. Ví dụ:

Tập xác định: D = R
Đạo hàm: y' = 3x² - 6x
Giải phương trình y' = 0: 3x² - 6x = 0 => x = 0 hoặc x = 2
...

Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

IV. Lưu Ý Khi Giải Bài Tập Khảo Sát Hàm Số

Luôn kiểm tra tập xác định của hàm số trước khi thực hiện các phép toán.
Tính đạo hàm chính xác và cẩn thận.
Kiểm tra dấu của đạo hàm để xác định loại cực trị.
Vẽ bảng biến thiên để hình dung được sự biến đổi của hàm số.

V. Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:

Bài tập 2.4 trang 64 SGK Toán 12 tập 1
Bài tập 2.5 trang 65 SGK Toán 12 tập 1

Chúc các em học tập tốt!

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.