Giải Bài Tập 1.27 Trang 36 SGK Toán 12 Tập 1

Giải bài tập 1.27 trang 36 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.27 trang 36 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập.

Chúng tôi sẽ cung cấp lời giải bài tập một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.

Trong Vật lý, điện trở tương đương \({R_{td}}\) của hai điện trở \({R_1},{R_2}\) mắc song song được xác định bởi công thức\(\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\). Biết rằng \({R_2} = 3\Omega \). Đặt \({R_1} = x(\Omega ),x > 0\). a) Tính \({R_{td}}\) theo \(x\), xem biểu thức tính được này là một hàm số \(y = f(x)\). Khảo sát sự biến thiên và vẽ đồ thị hàm số \(f(x)\) với \(x > 0\). b) Khi \(x\) tăng, điện trở \({R_{td}}\) thay đổi như thế nào? \({R_{td}}\) không thể vư

Đề bài

a) Tính \({R_{td}}\) theo \(x\), xem biểu thức tính được này là một hàm số \(y = f(x)\). Khảo sát sự biến thiên và vẽ đồ thị hàm số \(f(x)\) với \(x > 0\).

b) Khi \(x\) tăng, điện trở \({R_{td}}\) thay đổi như thế nào? \({R_{td}}\) không thể vượt qua giá trị bao nhiêu?

Phương pháp giải - Xem chi tiết Giải bài tập 1.27 trang 36 SGK Toán 12 tập 1 - Cùng khám phá 1

- Dùng công thức điện trở tương đương của hai điện trở mắc song song.

- Đưa \({R_{td}}\) về dạng hàm số y=f(x).

- Tìm tập xác định của hàm số

- Xét sự biến thiên của hàm số

- Vẽ đồ thị hàm số

- Phân tích sự thay đổi của \({R_{td}}\) khi x tăng.

Lời giải chi tiết

- Tính \({R_{td}}\) theo \(x\) :

\(\begin{array}{l}\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} = \frac{1}{x} + \frac{1}{3}\\\frac{1}{{{R_{td}}}} = \frac{{3 + x}}{{3x}}\\{R_{td}} = \frac{{3x}}{{3 + x}}\end{array}\)

Vậy hàm số cần khảo sát là: \(y = f(x) = \frac{{3x}}{{3 + x}}\)

- Tập xác định: \(D = \{ x > 0,x \in R\} \)

- Đạo hàm: \({f^\prime }(x) = \frac{d}{{dx}}\left( {\frac{{3x}}{{3 + x}}} \right) = \frac{{3(3 + x) - 3x}}{{{{(3 + x)}^2}}} = \frac{9}{{{{(3 + x)}^2}}} > 0\forall x \in R\)

Suy ra hàm số đồng biến trên khoảng \((0, + \infty )\).

- Giới hạn:

\(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{3x}}{{3 + x}} = 0\)

\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x}}{{3 + x}} = 3\)

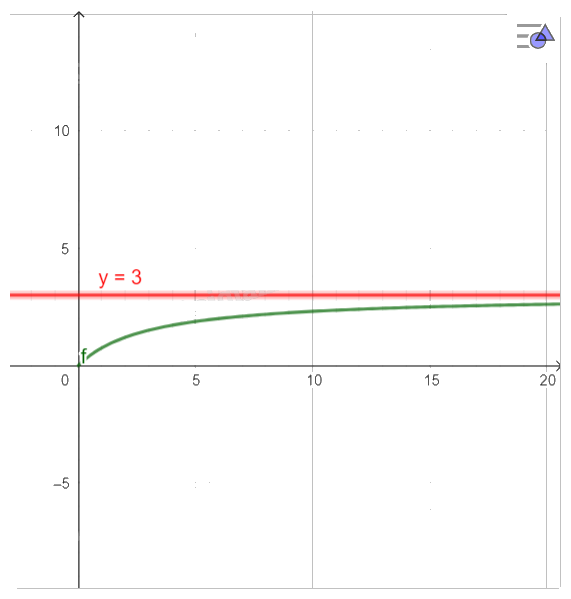
- Vẽ đồ thị:

Đồ thị hàm số 𝑓(𝑥) là đường cong đi qua các điểm (0,0) và (𝑥,𝑦) với 𝑥>0, tiệm cận ngang 𝑦=3.

Giải bài tập 1.27 trang 36 SGK Toán 12 tập 1 - Cùng khám phá 2

- Khi x tăng, \({R_{td}}\) cũng tăng nhưng tiệm cận về giá trị 3.

- Vậy, \({R_{td}}\) không thể vượt quá giá trị 3.

Giải Bài Tập 1.27 Trang 36 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 1.27 trang 36 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

Đề Bài Bài Tập 1.27 Trang 36 SGK Toán 12 Tập 1

Cho hàm số y = x³ - 3x² + 2. Hãy khảo sát hàm số và tìm các điểm cực trị.

Lời Giải Chi Tiết

Xác định tập xác định của hàm số: Hàm số y = x³ - 3x² + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
Tính đạo hàm cấp nhất: y' = 3x² - 6x
Tìm điểm dừng: Giải phương trình y' = 0, ta được: 3x² - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2. Vậy, các điểm dừng của hàm số là x₁ = 0 và x₂ = 2.
Khảo sát dấu của đạo hàm cấp nhất:
- Với x < 0, y' = 3x(x - 2) > 0, hàm số đồng biến.
- Với 0 < x < 2, y' = 3x(x - 2) < 0, hàm số nghịch biến.
- Với x > 2, y' = 3x(x - 2) > 0, hàm số đồng biến.
Kết luận về cực trị:
- Tại x = 0, y' đổi dấu từ dương sang âm, hàm số đạt cực đại và giá trị cực đại là y_CĐ = 0³ - 3(0)² + 2 = 2.
- Tại x = 2, y' đổi dấu từ âm sang dương, hàm số đạt cực tiểu và giá trị cực tiểu là y_CT = 2³ - 3(2)² + 2 = 0.
Tính đạo hàm cấp hai: y'' = 6x - 6
Tìm điểm uốn: Giải phương trình y'' = 0, ta được: 6x - 6 = 0 ⇔ x = 1.
Khảo sát dấu của đạo hàm cấp hai:
- Với x < 1, y'' < 0, hàm số lõm xuống.
- Với x > 1, y'' > 0, hàm số lồi lên.
Kết luận về điểm uốn: Tại x = 1, y'' đổi dấu, hàm số có điểm uốn. Giá trị y tại x = 1 là y = 1³ - 3(1)² + 2 = 0. Vậy, điểm uốn của hàm số là (1; 0).

Bảng Biến Thiên

x	-∞	0	2	+∞
y'	+	0	-	0	+
y	↗	2 (CĐ)	↘	0 (CT)	↗

Kết Luận

Hàm số y = x³ - 3x² + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là 0. Hàm số có điểm uốn tại (1; 0).

Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập khảo sát hàm số. Hãy luyện tập thêm nhiều bài tập khác để nâng cao kỹ năng giải toán của mình. Chúc các em học tốt!