Giải bài tập 2.2 trang 54 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 2.2 Trang 54 Toán 12 Tập 1 - Cùng Khám Phá
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.2 trang 54 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp kiến thức chính xác và dễ hiểu nhất.
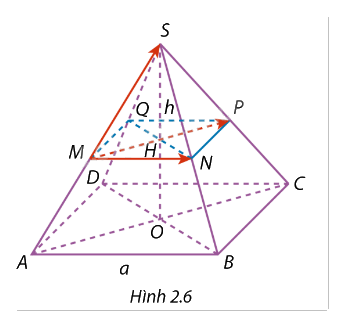
Cho hình chóp đều S.ABCD có cạnh đáy \(a\) và đường cao \(h\). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6). a) Trong những vectơ khác \(\vec O\), có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ: - Cùng hướng với \(\overrightarrow {MN} \); - Bằng \(\overrightarrow {MN} \). b) Tìm độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \) theo \(a\) và \(h\).
Đề bài
Cho hình chóp đều S.ABCD có cạnh đáy
\(a\) và đường cao \(h\). Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD và O, H lần lượt là tâm của các hình vuông ABCD, MNPQ (Hình 2.6).
a) Trong những vectơ khác \(\vec O\), có điểm đầu và điểm cuối là những điểm cho trên hình, hãy liệt kê các vectơ:
- Cùng hướng với \(\overrightarrow {MN} \);
- Bằng \(\overrightarrow {MN} \).
b) Tìm độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \) theo \(a\) và \(h\).
Phương pháp giải - Xem chi tiết
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết
a) Liệt kê các vectơ
- Cùng hướng với \(\overrightarrow {MN} \):
Vectơ cùng hướng với \(\overrightarrow {MN} \) là các vectơ có phương và chiều giống với \(\overrightarrow {MN} \), cụ thể là: \(\overrightarrow {QP} \), \(\overrightarrow {AB} \), \(\overrightarrow {DC} \).
- Bằng \(\overrightarrow {MN} \):
Vectơ bằng \(\overrightarrow {MN} \) là các vectơ có độ dài và phương chiều giống với \(\overrightarrow {MN} \), cụ thể là: \(\overrightarrow {QP} \)
b) Tính độ dài các vectơ \(\overrightarrow {MP} ,\overrightarrow {MS} \)
- Tính độ dài \(\overrightarrow {MP} \):
Ta xét tam giác đều SAC có MP là đường trung bình của tam giác đều SAC
\(MP = \frac{1}{2}AC = \frac{1}{2} \cdot a\sqrt 2 \) (AC là đường chéo của hình vuông ABCD)
Do đó: \(\overrightarrow {MP} = \frac{{a\sqrt 2 }}{2}\)
- Tính độ dài \(\overrightarrow {MS} \):
Ta xét tam giác vuông SOA với \(O\) là tâm của hình vuông đáy ABCD:
\(SA = \sqrt {{h^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Vì \(M\) là trung điểm của SA, ta có: \(SM = \frac{1}{2}SA = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Do đó: \(\overrightarrow {MS} = \frac{1}{2}\sqrt {{h^2} + \frac{{{a^2}}}{2}} \)
Giải Bài Tập 2.2 Trang 54 Toán 12 Tập 1 - Phương Pháp Giải Chi Tiết
Bài tập 2.2 trang 54 SGK Toán 12 tập 1 thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán liên quan đến việc tìm cực trị, khoảng đơn điệu của hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm cấp nhất: Tính f'(x) của hàm số.
- Tìm điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định.
- Khảo sát dấu của đạo hàm: Lập bảng xét dấu f'(x) để xác định khoảng hàm số đồng biến, nghịch biến.
- Kết luận về cực trị: Dựa vào bảng xét dấu, xác định các điểm cực đại, cực tiểu của hàm số.
Ví dụ Minh Họa Giải Bài Tập 2.2 Trang 54
Giả sử bài tập 2.2 yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên:
- Tập xác định: D = R
- Đạo hàm cấp nhất: y' = 3x2 - 6x
- Điểm tới hạn: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Bảng xét dấu:
x -∞ 0 2 +∞ y' + - + y NB ĐB NB - Kết luận: Hàm số đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2). Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Lưu Ý Quan Trọng Khi Giải Bài Tập
- Luôn kiểm tra lại các bước tính toán để tránh sai sót.
- Vẽ đồ thị hàm số để kiểm tra kết quả khảo sát.
- Nắm vững các định nghĩa và tính chất của đạo hàm.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Tusach.vn - Nguồn Tài Liệu Toán Học Uy Tín
tusach.vn tự hào là một trong những nguồn tài liệu toán học uy tín, cung cấp đầy đủ các bài giải, lý thuyết và bài tập trắc nghiệm cho học sinh THPT. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác cao. Hãy truy cập tusach.vn để đồng hành cùng chúng tôi trên con đường chinh phục môn Toán!
Các Bài Tập Liên Quan
- Giải bài tập 2.1 trang 54 SGK Toán 12 tập 1
- Giải bài tập 2.3 trang 54 SGK Toán 12 tập 1
- Bài tập trắc nghiệm về đạo hàm