Lý thuyết Vecto trong không gian Toán 12 Cùng khám phá
Tổng quan nội dung
Lý thuyết Vecto trong không gian Toán 12 - Nền tảng vững chắc cho kỳ thi
Lý thuyết Vecto trong không gian là một phần quan trọng của chương trình Toán 12, đóng vai trò then chốt trong việc giải quyết các bài toán về hình học không gian.
Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết, giúp bạn nắm vững kiến thức cơ bản và nâng cao về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong không gian.
1. Vecto trong không gian
1. Vecto trong không gian
| Vecto trong không gian là một đoạn thẳng có hướng. |
Ví dụ: Cho tứ diện ABCD. Hãy chỉ ra các vecto có điểm đầu A và điểm cuối là một trong các đỉnh còn lại của tứ diện.
Lời giải:
Ngoài đỉnh A, tứ diện còn có 3 đỉnh B, C, D nên ta có 3 vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \).
2. Độ dài của vecto. Hai vecto cùng phương, cùng hướng, bằng nhau
- Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vecto \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\). - Giá của vecto là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó. - Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau. - Nếu hai vecto cùng phương thì chúng có thể cùng hướng hoặc ngược hướng. - Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. - Nếu hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng nhau thì ta viết \(\overrightarrow a = \overrightarrow b \).. - Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. - Vecto đối của \(\overrightarrow a \) được kí hiệu là \( - \overrightarrow a \). |
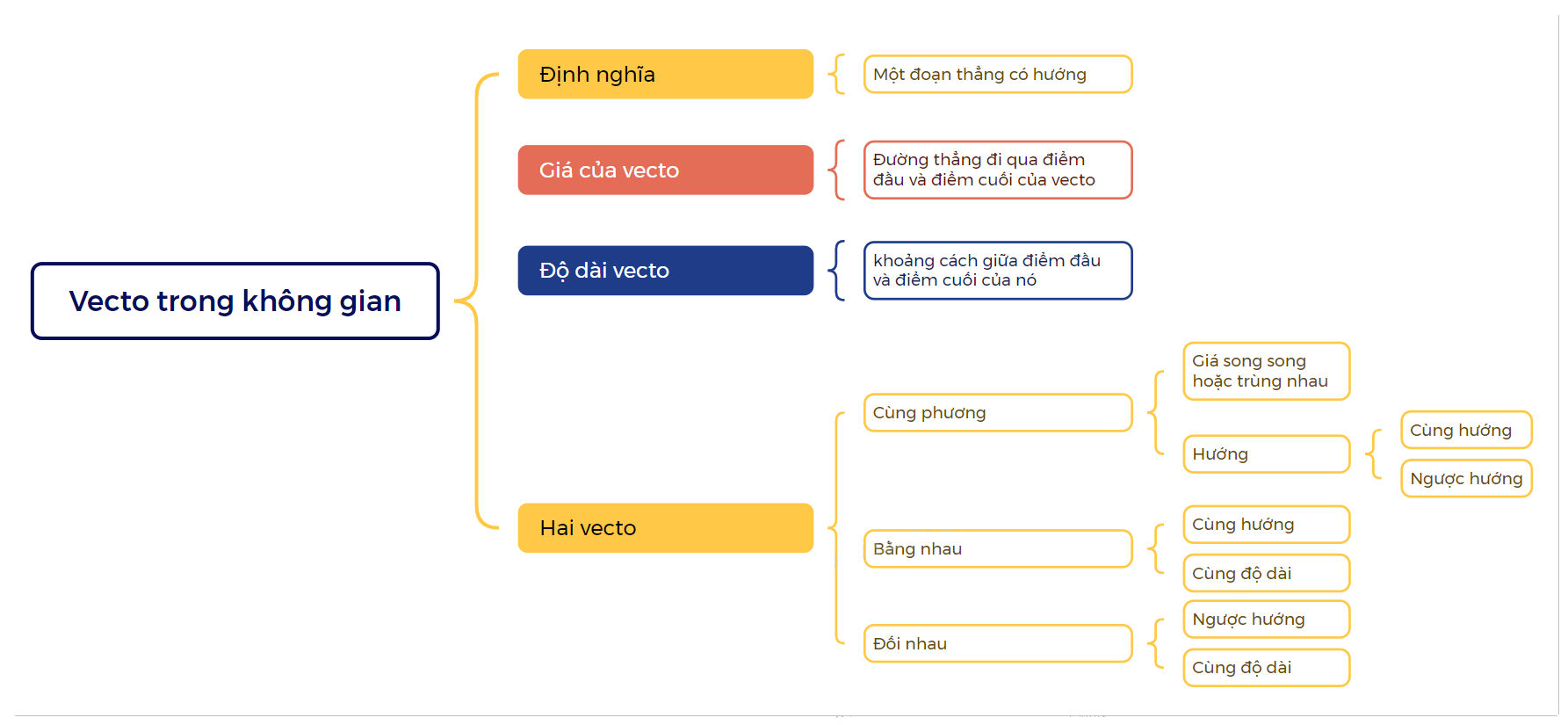
Lý Thuyết Vecto Trong Không Gian Toán 12: Tổng Quan Chi Tiết
Chương trình Toán 12, đặc biệt là phần Hình học không gian, đòi hỏi học sinh phải nắm vững kiến thức về vectơ. Lý thuyết Vecto trong không gian không chỉ là nền tảng để giải các bài toán về hình học mà còn là công cụ quan trọng trong nhiều lĩnh vực khoa học khác. Bài viết này của tusach.vn sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết này.
1. Khái Niệm Cơ Bản Về Vectơ Trong Không Gian
Vectơ trong không gian là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu là AB, trong đó A là điểm gốc và B là điểm cuối. Một vectơ có thể được biểu diễn bằng tọa độ trong một hệ tọa độ Oxyz, ví dụ: a = (x; y; z).
2. Các Phép Toán Vectơ
- Phép cộng vectơ:a + b = (xa + xb; ya + yb; za + zb)
- Phép trừ vectơ:a - b = (xa - xb; ya - yb; za - zb)
- Phép nhân vectơ với một số thực:k.a = (kxa; kya; kza)
3. Tích Vô Hướng
Tích vô hướng của hai vectơ a và b, ký hiệu là a.b, là một số thực được tính theo công thức:
a.b = xaxb + yayb + zazb
Ứng dụng của tích vô hướng:
- Tính góc giữa hai vectơ.
- Kiểm tra tính vuông góc của hai vectơ (a.b = 0).
- Tính hình chiếu của một vectơ lên một vectơ khác.
4. Tích Có Hướng
Tích có hướng của hai vectơ a và b, ký hiệu là a x b, là một vectơ có hướng vuông góc với cả hai vectơ a và b. Tích có hướng được tính bằng định thức:
| i | j | k | |
|---|---|---|---|
| xa | xb | xc | |
| ya | yb | yc | |
| za | zb | zc |
Ứng dụng của tích có hướng:
- Tính diện tích hình bình hành tạo bởi hai vectơ.
- Tìm vectơ pháp tuyến của một mặt phẳng.
5. Ứng Dụng Của Vectơ Trong Không Gian
Lý thuyết vectơ trong không gian có nhiều ứng dụng trong việc giải các bài toán về:
- Phương trình đường thẳng trong không gian.
- Phương trình mặt phẳng trong không gian.
- Khoảng cách giữa hai điểm, giữa điểm và đường thẳng, giữa điểm và mặt phẳng.
- Tính góc giữa hai đường thẳng, giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng.
6. Bài Tập Vận Dụng
Để nắm vững lý thuyết, bạn cần thực hành giải nhiều bài tập. Tusach.vn cung cấp một kho bài tập phong phú, đa dạng với đáp án chi tiết và phương pháp giải. Hãy truy cập tusach.vn để luyện tập ngay!
Kết Luận
Lý thuyết Vecto trong không gian Toán 12 là một phần kiến thức quan trọng, đòi hỏi sự hiểu biết sâu sắc và khả năng vận dụng linh hoạt. Hy vọng bài viết này của tusach.vn đã cung cấp cho bạn những kiến thức cần thiết để tự tin chinh phục môn Toán.