Giải mục 1 trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 54, 55, 56, 57, 58, 59 sách giáo khoa Toán 12 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu sâu sắc kiến thức, tự tin giải quyết các bài tập và đạt kết quả cao trong môn Toán.
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
LT2
Trả lời câu hỏi Luyện tập 2 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\).
a) Viết phương trình tham số của \(d\).
b) Tìm điểm \(M\) thuộc \(d\) biết \(OM = 7\).
Phương pháp giải:
a) Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Với \({M_0} = A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), thay vào ta được phương trình tham số của \(d\).
b) Tọa độ của \(M\) được biểu diễn theo tham số \(t\) từ phương trình tham số của \(d\). Dùng điều kiện \(OM = 7\), tức là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\), ta có:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay các tọa độ của \(M(x(t),y(t),z(t))\) từ phương trình tham số vào, rồi giải phương trình để tìm \(t\), từ đó suy ra tọa độ của \(M\).
Lời giải chi tiết:
a)
Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Với \(A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), phương trình tham số của đường thẳng \(d\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 6 + 2t}\\{y = - 2 + 2t}\\{z = 3 - t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b)
Điểm \(M\) có tọa độ \((x,y,z)\) thuộc đường thẳng \(d\), nên tọa độ của \(M\) được biểu diễn theo tham số \(t\) như sau:
\(M(6 + 2t, - 2 + 2t,3 - t)\)
Điều kiện \(OM = 7\) nghĩa là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\) bằng 7:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay tọa độ của \(M\) vào phương trình khoảng cách:
\(OM = \sqrt {{{(6 + 2t)}^2} + {{( - 2 + 2t)}^2} + {{(3 - t)}^2}} = 7\)
Bình phương hai vế:
\({(6 + 2t)^2} + {( - 2 + 2t)^2} + {(3 - t)^2} = 49\)
\({(6 + 2t)^2} = 36 + 24t + 4{t^2}\)
\({( - 2 + 2t)^2} = 4 - 8t + 4{t^2}\)
\({(3 - t)^2} = 9 - 6t + {t^2}\)
\((36 + 24t + 4{t^2}) + (4 - 8t + 4{t^2}) + (9 - 6t + {t^2}) = 49\)
\(49 + 10t + 9{t^2} = 49\)
\(10t + 9{t^2} = 0\)
\(t(9t + 10) = 0\)
Do đó, ta có hai nghiệm: \(t = 0\) và \(t = - \frac{{10}}{9}\)
Với \(t = 0\), tọa độ của \(M\) là:
\(M(6 + 2 \cdot 0, - 2 + 2 \cdot 0,3 - 0) = M(6, - 2,3)\)
Với \(t = - \frac{{10}}{9}\), tọa độ của \(M\) là:
\(M\left( {6 + 2 \cdot \left( { - \frac{{10}}{9}} \right), - 2 + 2 \cdot \left( { - \frac{{10}}{9}} \right),3 - \left( { - \frac{{10}}{9}} \right)} \right)\)
\(M\left( {6 - \frac{{20}}{9}, - 2 - \frac{{20}}{9},3 + \frac{{10}}{9}} \right) = M\left( {\frac{{54}}{9} - \frac{{20}}{9},\frac{{ - 18}}{9} - \frac{{20}}{9},\frac{{27}}{9} + \frac{{10}}{9}} \right)\)
\(M\left( {\frac{{34}}{9},\frac{{ - 38}}{9},\frac{{37}}{9}} \right)\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Phương trình tham số của đường thẳng là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Giả sử \({a_1},{a_2},{a_3}\) đều khác 0. Hãy tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Phương pháp giải:
Tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Lời giải chi tiết:
Từ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Ta có:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}} = t\)
Các tỉ số này đều bằng \(t\), điều này chứng tỏ tất cả các tỉ số này bằng nhau, và đường thẳng \(d\) có thể viết dưới dạng phương trình chính tắc:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) đi qua điểm \(N( - 2;3;1)\), có vectơ chỉ phương \(\vec a = (3; - 4;5)\).
a) Viết phương trình chính tắc của đường thẳng \(d\).
b) Tìm điểm \(A\) thuộc \(d\) biết \(A\) có hoành độ bằng 4.
Phương pháp giải:
a) Viết phương trình chính tắc của đường thẳng: Dựa vào phương trình tham số của đường thẳng và các tỉ số giữa tọa độ của điểm trên đường thẳng với tọa độ của điểm qua và các thành phần của vectơ chỉ phương.
b) Tìm điểm thuộc đường thẳng: Sử dụng điều kiện hoành độ của A để tìm tham số \(t\) trong phương trình tham số của đường thẳng. Từ đó tính ra tọa độ của điểm cần tìm.
Lời giải chi tiết:
a) Viết phương trình chính tắc của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 3t}\\{y = 3 - 4t}\\{z = 1 + 5t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x + 2}}{3} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 1}}{5}\)
b) Tìm điểm \(A\) thuộc \(d\) biết hoành độ của A là 4:
Điểm \(A\) thuộc \(d\) có tọa độ \(A(4;y;z)\).
Suy ra: \(t = \frac{{4 + 2}}{3} = 2\)
\(y = 3 - 4.2 = - 5\) và \(z = 1 + 5.2 = 11\)
Vậy điểm A có toạ độ là \(A(4; - 5;11)\)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\).
a) Vectơ \(\overrightarrow {AB} \) có phải là một vectơ chỉ phương của \(d\) không? Vì sao?
b) Viết phương trình tham số của đường thẳng \(d\).
c) Giả sử \({x_B} \ne {x_A},{y_B} \ne {y_A}\) và \({z_B} \ne {z_A}\), hãy viết phương trình chính tắc của \(d\).
Phương pháp giải:
a) Tìm vectơ \(\overrightarrow {AB} \), sau đó xác định xem vectơ này có phải là vectơ chỉ phương của đường thẳng \(d\).
b) Sử dụng tọa độ của điểm \(A\) hoặc \(B\) và vectơ chỉ phương \(\overrightarrow {AB} \) để viết phương trình tham số của đường thẳng.
c) Sử dụng tỉ số giữa các tọa độ và vectơ chỉ phương để viết phương trình chính tắc của đường thẳng d.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\):
Vectơ \(\overrightarrow {AB} \) được xác định bởi:
\(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\)
Hai điểm A, B đều thuộc đường thẳng d nên vectơ \(\overrightarrow {AB} \) cũng nằm trên đường thẳng d. Suy ra \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\).
b) Viết phương trình tham số của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) đi qua \(A({x_A};{y_A};{z_A})\) và có vectơ chỉ phương \(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_A} + ({x_B} - {x_A})t}\\{y = {y_A} + ({y_B} - {y_A})t}\\{z = {z_A} + ({z_B} - {z_A})t}\end{array}} \right.\quad (t \in \mathbb{R})\)
c) Viết phương trình chính tắc của đường thẳng \(d\):
Giả sử \({x_A} \ne {x_B},{y_A} \ne {y_B},{z_A} \ne {z_B}\), phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}}\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tam giác OAB với \(A(2; - 3;4)\), \(B( - 4;5;0)\). Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng AB và đường thẳng chứa đường trung tuyến kẻ từ O của tam giác OAB.
Phương pháp giải:
- Xác định vectơ chỉ phương của đường thẳng AB, chính là vectơ \(\overrightarrow {AB} \). Viết phương trình tham số của đường thẳng AB dựa trên điểm A hoặc B và vectơ chỉ phương \(\overrightarrow {AB} \). Từ phương trình tham số, lập phương trình chính tắc của đường thẳng AB.
- Xác định trung điểm M của đoạn thẳng AB. Viết phương trình đường thẳng đi qua O và M dựa trên tọa độ hai điểm này.
Lời giải chi tiết:
Xác định vectơ chỉ phương của đường thẳng AB:
\(\overrightarrow {AB} = B - A = ( - 4 - 2;5 + 3;0 - 4) = ( - 6;8; - 4)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(2; - 3;4)\) và có vectơ chỉ phương \(( - 6;8; - 4)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 6t}\\{y = - 3 + 8t}\\{z = 4 - 4t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng AB là:
\(\frac{{x - 2}}{{ - 6}} = \frac{{y + 3}}{8} = \frac{{z - 4}}{{ - 4}}\)
Trung điểm M của đoạn AB có tọa độ:
\(M = \left( {\frac{{2 + ( - 4)}}{2};\frac{{ - 3 + 5}}{2};\frac{{4 + 0}}{2}} \right) = ( - 1;1;2)\)
Phương trình tham số của đường thẳng đi qua \(O(0;0;0)\) và \(M( - 1;1;2)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = - t}\\{y = t}\\{z = 2t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng là:
\(\frac{x}{{ - 1}} = \frac{y}{1} = \frac{z}{2}\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 59 SGK Toán 12 Cùng khám phá
Anh Bình là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục Oxyz cho trước, anh Bình đang ngắm và ống kính ở vị trí A có tọa độ \((200;685;436)\) thì có một con gà lôi tía xuất hiện ở vị trí B có tọa độ \((640;550;474)\).
a) Viết phương trình tham số của đường thẳng chứa đoạn thẳng nối hai vị trí ống kính ngắm của anh Bình và con gà lôi tía.
b) Nếu một quả đồi có tọa độ đỉnh C là \((420;617,5;450)\). Hỏi C có thuộc đường ngắm AB không? Anh Bình có ngắm thấy con gà lôi tía này không?
Phương pháp giải:
a) Xác định vectơ chỉ phương của đường thẳng AB. Viết phương trình tham số của đường thẳng AB.
b) Thay toạ độ C vào phương trình tham số của đường thẳng AB. Xác định giá trị tham số t và kiểm tra xem các tọa độ của C có thỏa mãn không.
Lời giải chi tiết:
a) Vectơ chỉ phương của đường thẳng AB là:
\(\overrightarrow {AB} = (640 - 200;550 - 685;474 - 436) = (440; - 135;38)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(200;685;436)\) và có vectơ chỉ phương \(\overrightarrow {AB} = (440; - 135;38)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 200 + 440t}\\{y = 685 - 135t}\\{z = 436 + 38t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b) Thay tọa độ của \(C\) vào phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{420 = 200 + 440t}\\{617.5 = 685 - 135t}\\{450 = 436 + 38t}\end{array}} \right.\)
Giải phương trình:
\(t = \frac{{420 - 200}}{{440}} = \frac{{220}}{{440}} = 0.5\)
\(t = \frac{{685 - 617.5}}{{135}} = \frac{{67.5}}{{135}} = 0.5\)
\(t = \frac{{450 - 436}}{{38}} = \frac{{14}}{{38}} \approx 0.368\)
Kết luận: Giá trị \(t\) không giống nhau cho cả ba phương trình, do đó điểm \(C\) không thuộc đường thẳng AB. Và vì \(450 < 436 + 38.0,5 = 455\) nên C thấp hơn đường thẳng AB. Vậy quả đồi không chắn tầm nhìn nên anh Bình có thể ngắm thấy con gà lôi tía này.
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
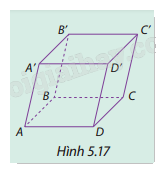
Phương pháp giải:
Tìm tất cả các cạnh song song hoặc trùng với cạnh AB.
Tìm các vectơ tương ứng với các cạnh đó, chính là các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp.
Lời giải chi tiết:
Vectơ đầu tiên là \(\overrightarrow {AB} \).
Các cạnh song song với AB gồm: A’B’, C’D’, CD.
Các vectơ khác \(\overrightarrow 0 \)có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB là:
\(\overrightarrow {AB} ,\quad \overrightarrow {A'B'} ,\quad \overrightarrow {CD} ,\quad \overrightarrow {C'D'} ,\quad \overrightarrow {BA} ,\quad \overrightarrow {B'A'} ,\quad \overrightarrow {DC} ,\quad \overrightarrow {D'C'} \).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 55 SGK Toán 12 Cùng khám phá
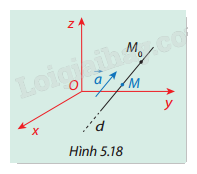
Trong không gian \(Oxyz\), cho đường thẳng \(d\) qua điểm \({M_0}({x_0};{y_0};{z_0})\), có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Giả sử \(M(x;y;z)\) là một điểm bất kỳ trên \(d\)(Hình 5.18). Ta biết \(\overrightarrow {{M_0}M} \) cùng phương với \(\vec a\) nên tồn tại số thực \(t\) sao cho \(\overrightarrow {{M_0}M} = t\vec a\).
a) Hãy tính tọa độ điểm \(M\) theo \({x_0},{y_0},{z_0},{a_1},{a_2},{a_3},t\).
b) Bạn An cho rằng điều kiện cần và đủ để \(M(x;y;z) \in d\) là:
\[\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\]
Bạn An phát biểu đúng hay không? Vì sao?
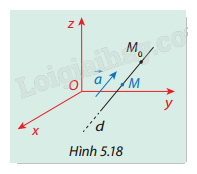
Phương pháp giải:
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Từ đó dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Lời giải chi tiết:
a)
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Vậy tọa độ của điểm \(M\) là:
\(M({x_0} + t{a_1},{y_0} + t{a_2},{z_0} + t{a_3})\)
b)
Vì d và \({M_0}M\) đều cùng song song với giá của vectơ \(\overrightarrow a \) nên d và \({M_0}M\) song song hoặc trùng nhau.
Mặt khác \({M_0} \in d\) suy ra \(M \in d\).
Vậy phát biểu của bạn An là đúng. Điều kiện để \(M(x,y,z) \in d\) là tồn tại t sao cho hệ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + t{a_1}}\\{y = {y_0} + t{a_2}}\\{z = {z_0} + t{a_3}}\end{array}} \right.\)
được thoả mãn.
LT1
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Tìm các vectơ có điểm đầu và điểm cuối trong các điểm S, A, B, C, D đã cho và là vectơ chỉ phương của d.
Phương pháp giải:
Sử dụng định nghĩa của vectơ chỉ phương: “Cho đường thẳng d, một vecto \(\overrightarrow u \)được gọi là VTCP của đường thẳng d nếu \(\overrightarrow u \) có giá song song hoặc trùng với đường thẳng d.”
Lời giải chi tiết:
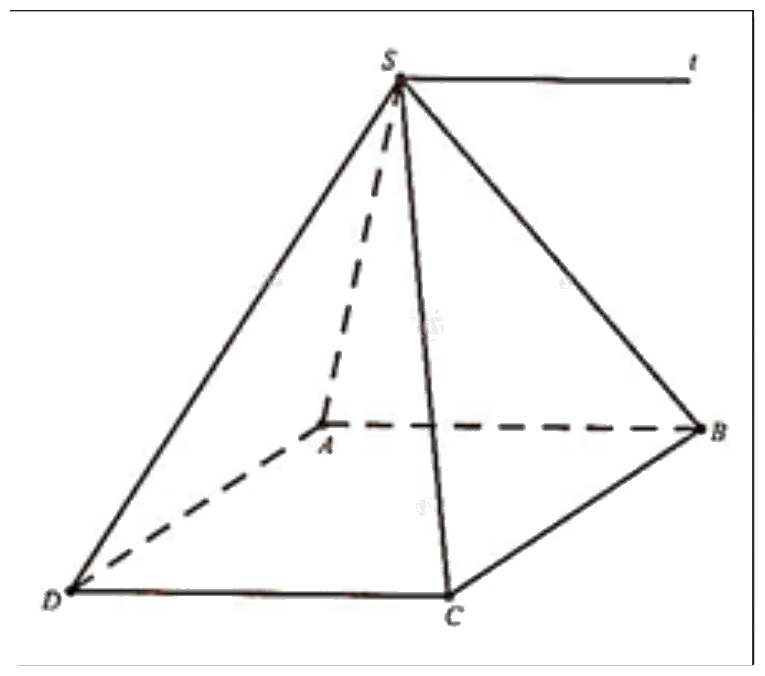
Từ hình vẽ ta thấy đường thẳng d song song với hai cạnh đáy AB và CD.
Suy ra vectơ chỉ phương của d là: \(\overrightarrow {AB} ,\,\,\overrightarrow {BA} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {DC} \).
- HĐ1
- LT1
- HĐ2
- LT2
- HĐ3
- LT3
- HĐ4
- LT4
- VD1
Trả lời câu hỏi Hoạt động 1 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.A'B'C'D' (Hình 5.17). Tìm bốn vectơ khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB.
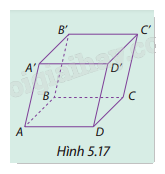
Phương pháp giải:
Tìm tất cả các cạnh song song hoặc trùng với cạnh AB.
Tìm các vectơ tương ứng với các cạnh đó, chính là các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp.
Lời giải chi tiết:
Vectơ đầu tiên là \(\overrightarrow {AB} \).
Các cạnh song song với AB gồm: A’B’, C’D’, CD.
Các vectơ khác \(\overrightarrow 0 \)có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp và có giá song song hoặc trùng với đường thẳng AB là:
\(\overrightarrow {AB} ,\quad \overrightarrow {A'B'} ,\quad \overrightarrow {CD} ,\quad \overrightarrow {C'D'} ,\quad \overrightarrow {BA} ,\quad \overrightarrow {B'A'} ,\quad \overrightarrow {DC} ,\quad \overrightarrow {D'C'} \).
Trả lời câu hỏi Luyện tập 1 trang 55 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Tìm các vectơ có điểm đầu và điểm cuối trong các điểm S, A, B, C, D đã cho và là vectơ chỉ phương của d.
Phương pháp giải:
Sử dụng định nghĩa của vectơ chỉ phương: “Cho đường thẳng d, một vecto \(\overrightarrow u \)được gọi là VTCP của đường thẳng d nếu \(\overrightarrow u \) có giá song song hoặc trùng với đường thẳng d.”
Lời giải chi tiết:
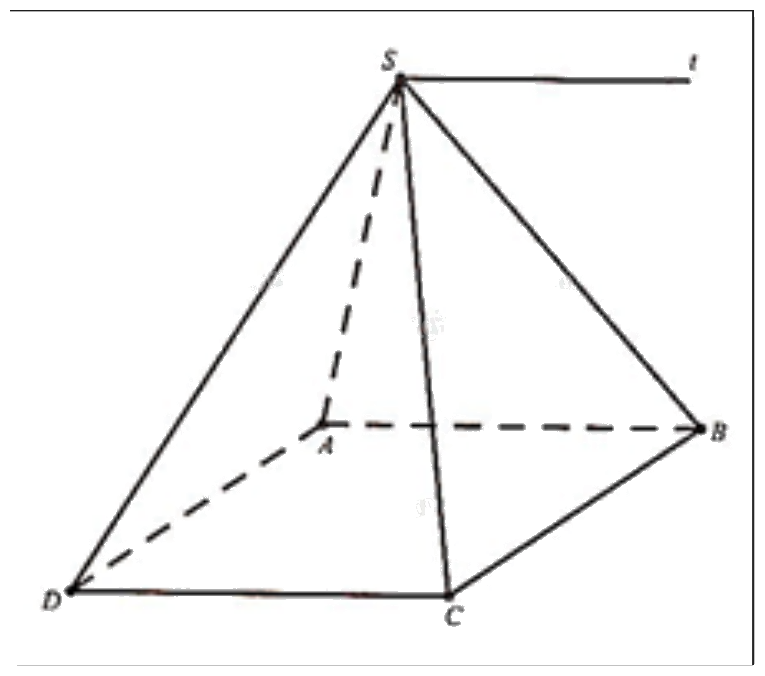
Từ hình vẽ ta thấy đường thẳng d song song với hai cạnh đáy AB và CD.
Suy ra vectơ chỉ phương của d là: \(\overrightarrow {AB} ,\,\,\overrightarrow {BA} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {DC} \).
Trả lời câu hỏi Hoạt động 2 trang 55 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) qua điểm \({M_0}({x_0};{y_0};{z_0})\), có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Giả sử \(M(x;y;z)\) là một điểm bất kỳ trên \(d\)(Hình 5.18). Ta biết \(\overrightarrow {{M_0}M} \) cùng phương với \(\vec a\) nên tồn tại số thực \(t\) sao cho \(\overrightarrow {{M_0}M} = t\vec a\).
a) Hãy tính tọa độ điểm \(M\) theo \({x_0},{y_0},{z_0},{a_1},{a_2},{a_3},t\).
b) Bạn An cho rằng điều kiện cần và đủ để \(M(x;y;z) \in d\) là:
\[\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\]
Bạn An phát biểu đúng hay không? Vì sao?
Phương pháp giải:
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Từ đó dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Lời giải chi tiết:
a)
Do \(\overrightarrow {{M_0}M} = t\vec a\), ta có:
\(\overrightarrow {{M_0}M} = (x - {x_0},y - {y_0},z - {z_0}) = t({a_1},{a_2},{a_3})\)
Dẫn đến hệ phương trình:
\(x = {x_0} + t{a_1},\,\,y = {y_0} + t{a_2},\,\,z = {z_0} + t{a_3}\)
Vậy tọa độ của điểm \(M\) là:
\(M({x_0} + t{a_1},{y_0} + t{a_2},{z_0} + t{a_3})\)
b)
Vì d và \({M_0}M\) đều cùng song song với giá của vectơ \(\overrightarrow a \) nên d và \({M_0}M\) song song hoặc trùng nhau.
Mặt khác \({M_0} \in d\) suy ra \(M \in d\).
Vậy phát biểu của bạn An là đúng. Điều kiện để \(M(x,y,z) \in d\) là tồn tại t sao cho hệ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + t{a_1}}\\{y = {y_0} + t{a_2}}\\{z = {z_0} + t{a_3}}\end{array}} \right.\)
được thoả mãn.
Trả lời câu hỏi Luyện tập 2 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\).
a) Viết phương trình tham số của \(d\).
b) Tìm điểm \(M\) thuộc \(d\) biết \(OM = 7\).
Phương pháp giải:
a) Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Với \({M_0} = A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), thay vào ta được phương trình tham số của \(d\).
b) Tọa độ của \(M\) được biểu diễn theo tham số \(t\) từ phương trình tham số của \(d\). Dùng điều kiện \(OM = 7\), tức là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\), ta có:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay các tọa độ của \(M(x(t),y(t),z(t))\) từ phương trình tham số vào, rồi giải phương trình để tìm \(t\), từ đó suy ra tọa độ của \(M\).
Lời giải chi tiết:
a)
Đường thẳng \(d\) đi qua điểm \(A(6; - 2;3)\) và có vectơ chỉ phương \(\vec a = (2;2; - 1)\). Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Với \(A(6; - 2;3)\) và \(\vec a = (2;2; - 1)\), phương trình tham số của đường thẳng \(d\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 6 + 2t}\\{y = - 2 + 2t}\\{z = 3 - t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b)
Điểm \(M\) có tọa độ \((x,y,z)\) thuộc đường thẳng \(d\), nên tọa độ của \(M\) được biểu diễn theo tham số \(t\) như sau:
\(M(6 + 2t, - 2 + 2t,3 - t)\)
Điều kiện \(OM = 7\) nghĩa là khoảng cách từ gốc tọa độ \(O(0;0;0)\) đến \(M\) bằng 7:
\(OM = \sqrt {{x^2} + {y^2} + {z^2}} = 7\)
Thay tọa độ của \(M\) vào phương trình khoảng cách:
\(OM = \sqrt {{{(6 + 2t)}^2} + {{( - 2 + 2t)}^2} + {{(3 - t)}^2}} = 7\)
Bình phương hai vế:
\({(6 + 2t)^2} + {( - 2 + 2t)^2} + {(3 - t)^2} = 49\)
\({(6 + 2t)^2} = 36 + 24t + 4{t^2}\)
\({( - 2 + 2t)^2} = 4 - 8t + 4{t^2}\)
\({(3 - t)^2} = 9 - 6t + {t^2}\)
\((36 + 24t + 4{t^2}) + (4 - 8t + 4{t^2}) + (9 - 6t + {t^2}) = 49\)
\(49 + 10t + 9{t^2} = 49\)
\(10t + 9{t^2} = 0\)
\(t(9t + 10) = 0\)
Do đó, ta có hai nghiệm: \(t = 0\) và \(t = - \frac{{10}}{9}\)
Với \(t = 0\), tọa độ của \(M\) là:
\(M(6 + 2 \cdot 0, - 2 + 2 \cdot 0,3 - 0) = M(6, - 2,3)\)
Với \(t = - \frac{{10}}{9}\), tọa độ của \(M\) là:
\(M\left( {6 + 2 \cdot \left( { - \frac{{10}}{9}} \right), - 2 + 2 \cdot \left( { - \frac{{10}}{9}} \right),3 - \left( { - \frac{{10}}{9}} \right)} \right)\)
\(M\left( {6 - \frac{{20}}{9}, - 2 - \frac{{20}}{9},3 + \frac{{10}}{9}} \right) = M\left( {\frac{{54}}{9} - \frac{{20}}{9},\frac{{ - 18}}{9} - \frac{{20}}{9},\frac{{27}}{9} + \frac{{10}}{9}} \right)\)
\(M\left( {\frac{{34}}{9},\frac{{ - 38}}{9},\frac{{37}}{9}} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 56 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương \(\vec a = ({a_1};{a_2};{a_3})\). Phương trình tham số của đường thẳng là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Giả sử \({a_1},{a_2},{a_3}\) đều khác 0. Hãy tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Phương pháp giải:
Tính các tỉ số \(\frac{{x - {x_0}}}{{{a_1}}},\frac{{y - {y_0}}}{{{a_2}}},\frac{{z - {z_0}}}{{{a_3}}}\) theo \(t\) và so sánh các tỉ số này.
Lời giải chi tiết:
Từ phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + {a_1}t}\\{y = {y_0} + {a_2}t}\\{z = {z_0} + {a_3}t}\end{array}} \right.\)
Ta có:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}} = t\)
Các tỉ số này đều bằng \(t\), điều này chứng tỏ tất cả các tỉ số này bằng nhau, và đường thẳng \(d\) có thể viết dưới dạng phương trình chính tắc:
\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\)
Trả lời câu hỏi Luyện tập 3 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) đi qua điểm \(N( - 2;3;1)\), có vectơ chỉ phương \(\vec a = (3; - 4;5)\).
a) Viết phương trình chính tắc của đường thẳng \(d\).
b) Tìm điểm \(A\) thuộc \(d\) biết \(A\) có hoành độ bằng 4.
Phương pháp giải:
a) Viết phương trình chính tắc của đường thẳng: Dựa vào phương trình tham số của đường thẳng và các tỉ số giữa tọa độ của điểm trên đường thẳng với tọa độ của điểm qua và các thành phần của vectơ chỉ phương.
b) Tìm điểm thuộc đường thẳng: Sử dụng điều kiện hoành độ của A để tìm tham số \(t\) trong phương trình tham số của đường thẳng. Từ đó tính ra tọa độ của điểm cần tìm.
Lời giải chi tiết:
a) Viết phương trình chính tắc của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) có dạng:
\(\left\{ {\begin{array}{*{20}{l}}{x = - 2 + 3t}\\{y = 3 - 4t}\\{z = 1 + 5t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x + 2}}{3} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 1}}{5}\)
b) Tìm điểm \(A\) thuộc \(d\) biết hoành độ của A là 4:
Điểm \(A\) thuộc \(d\) có tọa độ \(A(4;y;z)\).
Suy ra: \(t = \frac{{4 + 2}}{3} = 2\)
\(y = 3 - 4.2 = - 5\) và \(z = 1 + 5.2 = 11\)
Vậy điểm A có toạ độ là \(A(4; - 5;11)\)
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho đường thẳng \(d\) qua hai điểm phân biệt \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\).
a) Vectơ \(\overrightarrow {AB} \) có phải là một vectơ chỉ phương của \(d\) không? Vì sao?
b) Viết phương trình tham số của đường thẳng \(d\).
c) Giả sử \({x_B} \ne {x_A},{y_B} \ne {y_A}\) và \({z_B} \ne {z_A}\), hãy viết phương trình chính tắc của \(d\).
Phương pháp giải:
a) Tìm vectơ \(\overrightarrow {AB} \), sau đó xác định xem vectơ này có phải là vectơ chỉ phương của đường thẳng \(d\).
b) Sử dụng tọa độ của điểm \(A\) hoặc \(B\) và vectơ chỉ phương \(\overrightarrow {AB} \) để viết phương trình tham số của đường thẳng.
c) Sử dụng tỉ số giữa các tọa độ và vectơ chỉ phương để viết phương trình chính tắc của đường thẳng d.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\):
Vectơ \(\overrightarrow {AB} \) được xác định bởi:
\(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\)
Hai điểm A, B đều thuộc đường thẳng d nên vectơ \(\overrightarrow {AB} \) cũng nằm trên đường thẳng d. Suy ra \(\overrightarrow {AB} \) là vectơ chỉ phương của đường thẳng \(d\).
b) Viết phương trình tham số của đường thẳng \(d\):
Phương trình tham số của đường thẳng \(d\) đi qua \(A({x_A};{y_A};{z_A})\) và có vectơ chỉ phương \(\overrightarrow {AB} = ({x_B} - {x_A},{y_B} - {y_A},{z_B} - {z_A})\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = {x_A} + ({x_B} - {x_A})t}\\{y = {y_A} + ({y_B} - {y_A})t}\\{z = {z_A} + ({z_B} - {z_A})t}\end{array}} \right.\quad (t \in \mathbb{R})\)
c) Viết phương trình chính tắc của đường thẳng \(d\):
Giả sử \({x_A} \ne {x_B},{y_A} \ne {y_B},{z_A} \ne {z_B}\), phương trình chính tắc của đường thẳng \(d\) là:
\(\frac{{x - {x_A}}}{{{x_B} - {x_A}}} = \frac{{y - {y_A}}}{{{y_B} - {y_A}}} = \frac{{z - {z_A}}}{{{z_B} - {z_A}}}\)
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tam giác OAB với \(A(2; - 3;4)\), \(B( - 4;5;0)\). Viết phương trình tham số và phương trình chính tắc (nếu có) của đường thẳng AB và đường thẳng chứa đường trung tuyến kẻ từ O của tam giác OAB.
Phương pháp giải:
- Xác định vectơ chỉ phương của đường thẳng AB, chính là vectơ \(\overrightarrow {AB} \). Viết phương trình tham số của đường thẳng AB dựa trên điểm A hoặc B và vectơ chỉ phương \(\overrightarrow {AB} \). Từ phương trình tham số, lập phương trình chính tắc của đường thẳng AB.
- Xác định trung điểm M của đoạn thẳng AB. Viết phương trình đường thẳng đi qua O và M dựa trên tọa độ hai điểm này.
Lời giải chi tiết:
Xác định vectơ chỉ phương của đường thẳng AB:
\(\overrightarrow {AB} = B - A = ( - 4 - 2;5 + 3;0 - 4) = ( - 6;8; - 4)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(2; - 3;4)\) và có vectơ chỉ phương \(( - 6;8; - 4)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 2 - 6t}\\{y = - 3 + 8t}\\{z = 4 - 4t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng AB là:
\(\frac{{x - 2}}{{ - 6}} = \frac{{y + 3}}{8} = \frac{{z - 4}}{{ - 4}}\)
Trung điểm M của đoạn AB có tọa độ:
\(M = \left( {\frac{{2 + ( - 4)}}{2};\frac{{ - 3 + 5}}{2};\frac{{4 + 0}}{2}} \right) = ( - 1;1;2)\)
Phương trình tham số của đường thẳng đi qua \(O(0;0;0)\) và \(M( - 1;1;2)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = - t}\\{y = t}\\{z = 2t}\end{array}} \right.\quad (t \in \mathbb{R})\)
Phương trình chính tắc của đường thẳng là:
\(\frac{x}{{ - 1}} = \frac{y}{1} = \frac{z}{2}\)
Trả lời câu hỏi Vận dụng 1 trang 59 SGK Toán 12 Cùng khám phá
Anh Bình là một nhiếp ảnh gia chuyên săn ảnh chim hoang dã. Giả sử với hệ trục Oxyz cho trước, anh Bình đang ngắm và ống kính ở vị trí A có tọa độ \((200;685;436)\) thì có một con gà lôi tía xuất hiện ở vị trí B có tọa độ \((640;550;474)\).
a) Viết phương trình tham số của đường thẳng chứa đoạn thẳng nối hai vị trí ống kính ngắm của anh Bình và con gà lôi tía.
b) Nếu một quả đồi có tọa độ đỉnh C là \((420;617,5;450)\). Hỏi C có thuộc đường ngắm AB không? Anh Bình có ngắm thấy con gà lôi tía này không?
Phương pháp giải:
a) Xác định vectơ chỉ phương của đường thẳng AB. Viết phương trình tham số của đường thẳng AB.
b) Thay toạ độ C vào phương trình tham số của đường thẳng AB. Xác định giá trị tham số t và kiểm tra xem các tọa độ của C có thỏa mãn không.
Lời giải chi tiết:
a) Vectơ chỉ phương của đường thẳng AB là:
\(\overrightarrow {AB} = (640 - 200;550 - 685;474 - 436) = (440; - 135;38)\)
Phương trình tham số của đường thẳng AB đi qua điểm \(A(200;685;436)\) và có vectơ chỉ phương \(\overrightarrow {AB} = (440; - 135;38)\) là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 200 + 440t}\\{y = 685 - 135t}\\{z = 436 + 38t}\end{array}} \right.\quad (t \in \mathbb{R})\)
b) Thay tọa độ của \(C\) vào phương trình tham số:
\(\left\{ {\begin{array}{*{20}{l}}{420 = 200 + 440t}\\{617.5 = 685 - 135t}\\{450 = 436 + 38t}\end{array}} \right.\)
Giải phương trình:
\(t = \frac{{420 - 200}}{{440}} = \frac{{220}}{{440}} = 0.5\)
\(t = \frac{{685 - 617.5}}{{135}} = \frac{{67.5}}{{135}} = 0.5\)
\(t = \frac{{450 - 436}}{{38}} = \frac{{14}}{{38}} \approx 0.368\)
Kết luận: Giá trị \(t\) không giống nhau cho cả ba phương trình, do đó điểm \(C\) không thuộc đường thẳng AB. Và vì \(450 < 436 + 38.0,5 = 455\) nên C thấp hơn đường thẳng AB. Vậy quả đồi không chắn tầm nhìn nên anh Bình có thể ngắm thấy con gà lôi tía này.
Giải mục 1 trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2 - Cùng khám phá
Mục 1 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các khái niệm cơ bản, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của Mục 1
- Đạo hàm của hàm số: Định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc đạo hàm của tổng, hiệu, tích, thương, và hàm hợp.
- Đạo hàm của các hàm số thường gặp: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit.
- Ứng dụng của đạo hàm: Khảo sát hàm số (tìm cực trị, điểm uốn, khoảng đơn điệu).
Giải chi tiết các bài tập trang 54, 55, 56, 57, 58, 59
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1, trang 54, 55, 56, 57, 58, 59 SGK Toán 12 tập 2:
Bài 1 (Trang 54)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Bài 2 (Trang 55)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x).
Lời giải:
g'(x) = cos(x) - sin(x)
Bài 3 (Trang 56)
Đề bài: Tìm đạo hàm của hàm số h(x) = ex + ln(x).
Lời giải:
h'(x) = ex + 1/x
Bài 4 (Trang 57)
Đề bài: Cho hàm số y = x2 - 4x + 3. Tìm các điểm cực trị của hàm số.
Lời giải:
y' = 2x - 4. Giải phương trình y' = 0, ta được x = 2. Kiểm tra dấu của y' xung quanh x = 2, ta thấy hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y(2) = -1.
Bài 5 (Trang 58)
Đề bài: Khảo sát hàm số y = x3 - 3x2 + 2x.
Lời giải:
y' = 3x2 - 6x + 2. Giải phương trình y' = 0, ta được x1 = (3 - √3)/3 và x2 = (3 + √3)/3. Khảo sát dấu của y' và y'' để xác định các điểm cực trị và điểm uốn của hàm số.
Bài 6 (Trang 59)
Đề bài: Tìm khoảng đơn điệu của hàm số y = x4 - 4x2 + 1.
Lời giải:
y' = 4x3 - 8x = 4x(x2 - 2). Giải phương trình y' = 0, ta được x = 0, x = √2, x = -√2. Khảo sát dấu của y' trên các khoảng xác định để xác định khoảng đồng biến và nghịch biến của hàm số.
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các quy tắc tính đạo hàm.
- Sử dụng đúng công thức đạo hàm của các hàm số thường gặp.
- Kiểm tra lại kết quả tính đạo hàm.
- Áp dụng đạo hàm để giải quyết các bài toán thực tế.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về Mục 1 SGK Toán 12 tập 2 và tự tin giải quyết các bài tập tương tự. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ!