Giải mục 3 trang 19, 20, 21 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 3 trang 19, 20, 21 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với phần giải bài tập mục 3 trang 19, 20, 21 SGK Toán 12 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chi tiết và dễ hiểu nhất.
Mục 3 tập trung vào các kiến thức về hàm số và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học tiếp theo.
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số (y = f(x) = x + frac{x}{{{x^2} - 1}}) và đường thẳng (Delta :y = x) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và(Delta ) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi(x to - infty ) và (x to + infty )
LT3
Trả lời câu hỏi Luyện tập 3 trang 20 SGK Toán 12 Cùng khám phá
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
Phương pháp giải:
Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)
Lời giải chi tiết:
Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 20 SGK Toán 12 Cùng khám phá
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
Phương pháp giải:
Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Lời giải chi tiết:
Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 19 SGK Toán 12 Cùng khám phá
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
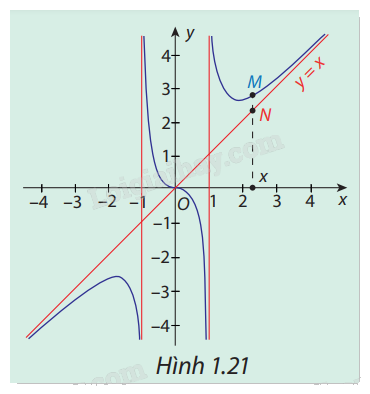
Phương pháp giải:
Nhìn vào đồ thị rồi nhận xét.
Lời giải chi tiết:
Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
VD2
Trả lời câu hỏi Vận dụng 2 trang 21 SGK Toán 12 Cùng khám phá
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
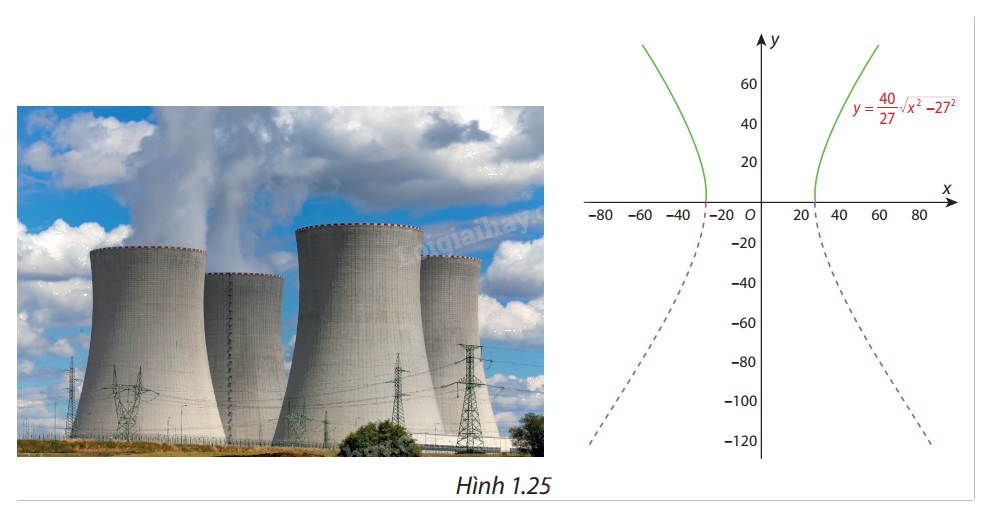
Phương pháp giải:
Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
- HĐ3
- LT3
- VD1
- VD2
Trả lời câu hỏi Hoạt động 3 trang 19 SGK Toán 12 Cùng khám phá
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
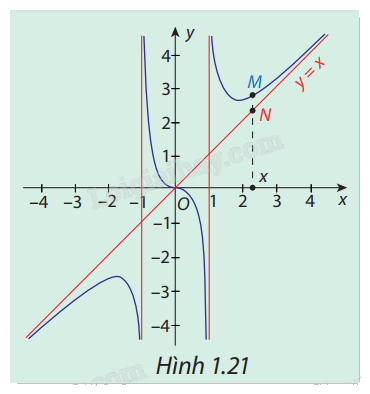
Phương pháp giải:
Nhìn vào đồ thị rồi nhận xét.
Lời giải chi tiết:
Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
Trả lời câu hỏi Luyện tập 3 trang 20 SGK Toán 12 Cùng khám phá
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
Phương pháp giải:
Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)
Lời giải chi tiết:
Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
Trả lời câu hỏi Vận dụng 1 trang 20 SGK Toán 12 Cùng khám phá
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
Phương pháp giải:
Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Lời giải chi tiết:
Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
Trả lời câu hỏi Vận dụng 2 trang 21 SGK Toán 12 Cùng khám phá
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
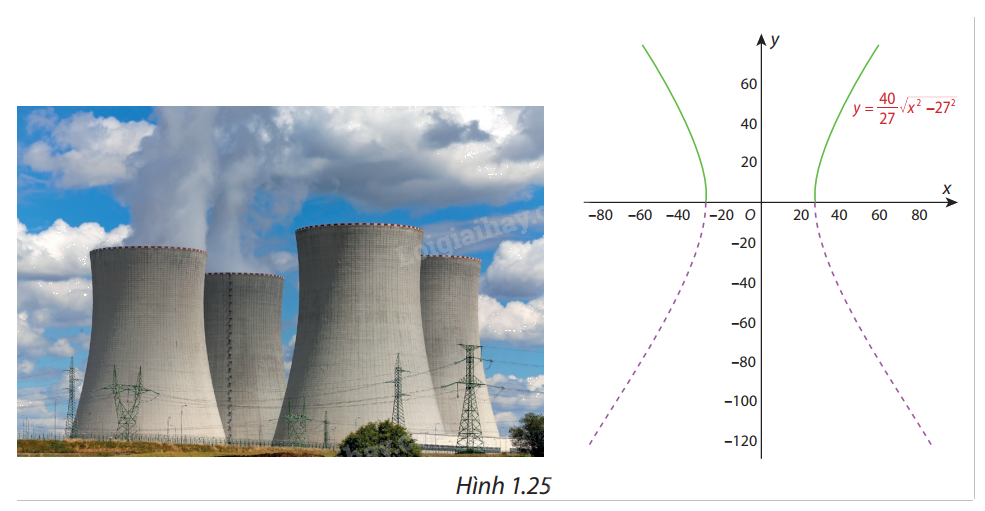
Phương pháp giải:
Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
Giải mục 3 trang 19, 20, 21 SGK Toán 12 tập 1: Tổng quan và hướng dẫn chi tiết
Mục 3 của SGK Toán 12 tập 1 tập trung vào việc vận dụng kiến thức về đạo hàm để khảo sát hàm số bậc ba. Đây là một phần quan trọng trong chương trình học, giúp học sinh hiểu rõ hơn về tính chất của hàm số và cách xác định các điểm cực trị, điểm uốn. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 3, trang 19, 20, 21, kèm theo các lưu ý quan trọng để giúp các em nắm vững kiến thức.
Nội dung chính của mục 3
- Khái niệm về điểm cực trị: Điểm cực đại, điểm cực tiểu và điều kiện để hàm số đạt cực trị.
- Cách tìm điểm cực trị: Sử dụng đạo hàm bậc nhất để tìm các điểm nghi ngờ là cực trị, sau đó kiểm tra bằng đạo hàm bậc hai.
- Khái niệm về điểm uốn: Điểm uốn và điều kiện để hàm số có điểm uốn.
- Cách tìm điểm uốn: Sử dụng đạo hàm bậc hai để tìm các điểm nghi ngờ là điểm uốn.
- Ứng dụng của đạo hàm trong việc khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn và vẽ đồ thị hàm số.
Giải chi tiết các bài tập
Bài 1: (Trang 19)
Đề bài: Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải:
- Xác định tập xác định: Tập xác định của hàm số là R.
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x.
- Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
- Xác định loại cực trị:
- Tại x = 0, y'' = 6x - 6 = -6 < 0, hàm số đạt cực đại tại x = 0, ymax = 2.
- Tại x = 2, y'' = 6x - 6 = 6 > 0, hàm số đạt cực tiểu tại x = 2, ymin = -2.
- Tính đạo hàm bậc hai: y'' = 6x - 6.
- Tìm điểm uốn: Giải phương trình y'' = 0, ta được x = 1.
- Kết luận: Hàm số có điểm uốn tại x = 1, y = 0.
Bài 2: (Trang 20)
Đề bài: Khảo sát hàm số y = -x3 + 3x2 - 1.
Lời giải: (Tương tự như bài 1, thực hiện các bước tương tự để khảo sát hàm số)
Bài 3: (Trang 21)
Đề bài: Khảo sát hàm số y = x3 - 6x2 + 9x.
Lời giải: (Tương tự như bài 1, thực hiện các bước tương tự để khảo sát hàm số)
Lưu ý khi giải bài tập khảo sát hàm số
- Luôn xác định đúng tập xác định của hàm số.
- Tính đạo hàm chính xác và cẩn thận.
- Kiểm tra kỹ điều kiện để hàm số đạt cực trị và điểm uốn.
- Vẽ đồ thị hàm số để kiểm tra lại kết quả.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn khi giải các bài tập khảo sát hàm số trong SGK Toán 12 tập 1. Chúc các em học tập tốt!