Giải bài tập 3.8 trang 103 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải bài tập 3.8 trang 103 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 3.8 trang 103 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn sẽ giúp các em hiểu rõ phương pháp giải và nắm vững kiến thức cần thiết để giải quyết các bài toán tương tự.
Trong 30 ngày, một nhà đầu tư đã theo dõi giá cổ phiếu của hai công ty G và H vào phiên mở cửa mỗi ngày. Thông tin được ghi lại ở hai bảng dưới đây:
Đề bài
Trong 30 ngày, một nhà đầu tư đã theo dõi giá cổ phiếu của hai công ty G và H vào phiên mở cửa mỗi ngày. Thông tin được ghi lại ở hai bảng dưới đây:
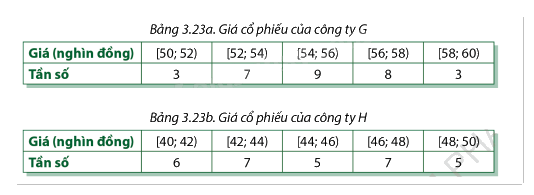
Giá cổ phiếu của công ty nào ít biến động hơn (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
Áp dụng các công thức sau để tính độ lệch chuẩn giá cổ phiếu của công ty G và H. Sau đó lấy hai giá trị này đem so sánh, công ty nào có độ lệch chuẩn thấp hơn thì giá cổ phiếu của công ty đó ít biến động hơn.
- Công thức tính trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)
Lời giải chi tiết
Theo đề bài, ta có N = 30.
Công ty G:

- Giá cổ phiếu trung bình là:
\({\bar x_G} = \frac{{51.3 + 53.7 + 55.9 + 57.8 + 59.3}}{{30}} \approx 55,07\)
- Tính \(\overline {x_G^2} \):
\(\overline {x_G^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{51}^2}.3 + {{53}^2}.7 + {{55}^2}.9 + {{57}^2}.8 + {{59}^2}.3}}{{30}} \approx 3037,53\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_G} = \sqrt {\overline {x_G^2} - {{\left( {{{\overline x }_G}} \right)}^2}} = \sqrt {3037,53 - 55,{{07}^2}} \approx 2,197\)
Công ty H:

- Giá cổ phiếu trung bình là:
\({\bar x_H} = \frac{{41.6 + 43.7 + 45.5 + 47.7 + 49.5}}{{30}} \approx 44,87\)
- Tính \(\overline {x_H^2} \):
\(\overline {x_H^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{41}^2}.6 + {{43}^2}.7 + {{45}^2}.5 + {{47}^2}.7 + {{49}^2}.5}}{{30}} \approx 2020,73\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_H} = \sqrt {\overline {x_H^2} - {{\left( {{{\overline x }_H}} \right)}^2}} = \sqrt {2020,73 - 44,{{87}^2}} \approx 2,777\)
Vì \({S_G} < {S_H}\) nên giá cổ phiếu của công ty G ít biến động hơn.
Giải bài tập 3.8 trang 103 SGK Toán 12 tập 1: Đề bài
Bài tập 3.8 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Cụ thể, đề bài thường cho một hàm số và yêu cầu:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất và tìm các điểm tới hạn (điểm mà đạo hàm bằng 0 hoặc không xác định).
- Lập bảng biến thiên của hàm số.
- Xác định các khoảng đơn điệu của hàm số.
- Tìm các điểm cực trị (cực đại, cực tiểu) của hàm số.
Phương pháp giải bài tập 3.8 trang 103 SGK Toán 12 tập 1
Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Bước 1: Xác định tập xác định: Tìm miền xác định của hàm số, tức là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Bước 2: Tính đạo hàm bậc nhất: Sử dụng các quy tắc đạo hàm để tính đạo hàm f'(x) của hàm số.
- Bước 3: Tìm điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các giá trị của x mà đạo hàm bằng 0. Ngoài ra, cần kiểm tra các điểm mà đạo hàm không xác định.
- Bước 4: Lập bảng biến thiên: Dựa vào các điểm tới hạn, chia tập xác định thành các khoảng và xét dấu của đạo hàm f'(x) trên mỗi khoảng. Từ đó, xác định các khoảng đơn điệu của hàm số (đồng biến, nghịch biến).
- Bước 5: Xác định cực trị: Sử dụng bảng biến thiên để xác định các điểm cực trị của hàm số. Nếu f'(x) đổi dấu từ dương sang âm tại một điểm x, thì đó là điểm cực đại. Nếu f'(x) đổi dấu từ âm sang dương tại một điểm x, thì đó là điểm cực tiểu.
Ví dụ minh họa giải bài tập 3.8 trang 103 SGK Toán 12 tập 1
Giả sử hàm số cần khảo sát là: f(x) = x3 - 3x2 + 2
Bước 1: Tập xác định: Hàm số xác định trên R.
Bước 2: Đạo hàm bậc nhất: f'(x) = 3x2 - 6x
Bước 3: Điểm tới hạn: Giải phương trình 3x2 - 6x = 0, ta được x = 0 và x = 2.
Bước 4: Bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | ↗ | ↘ | ↗ |
Bước 5: Cực trị:
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, nên x = 0 là điểm cực đại và f(0) = 2.
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, nên x = 2 là điểm cực tiểu và f(2) = -2.
Lưu ý khi giải bài tập 3.8 trang 103 SGK Toán 12 tập 1
- Luôn kiểm tra kỹ tập xác định của hàm số.
- Tính đạo hàm chính xác và cẩn thận.
- Lập bảng biến thiên một cách chi tiết và rõ ràng.
- Kết luận đúng về các khoảng đơn điệu và cực trị của hàm số.
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết bài tập 3.8 trang 103 SGK Toán 12 tập 1 một cách dễ dàng. Chúc các em học tập tốt!