Giải mục 1 trang 41, 42, 43 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 41, 42, 43 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết Giải mục 1 trang 41, 42, 43 SGK Toán 12 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 1 trong chương trình Toán 12 tập 2 thường xoay quanh các kiến thức về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số. Chúng tôi sẽ giúp các em hiểu rõ từng bước giải, từ đó củng cố kiến thức và tự tin hơn trong các bài kiểm tra.
Xét các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp chữ nhật \(ABCD.A'B'C'D'\) (Hình 5.1). a) Tìm bốn vectơ có giá trị vuông góc với mặt phẳng \((ABCD)\). b) Tìm hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \((ABCD)\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 43 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tứ diện \(ABCD\) có các đỉnh là \(A(5;1;3)\), \(B(1;6;2)\), \(C(5;0;4)\) và \(D(4;0;6)\). Tìm một vectơ pháp tuyến của mặt phẳng \((\alpha )\) chứa cạnh \(AB\) và song song với cạnh \(CD\).
Phương pháp giải:
Vì mặt phẳng \((\alpha )\) chứa cạnh \(AB\) và song song với cạnh \(CD\), nên vectơ pháp tuyến của mặt phẳng \((\alpha )\) sẽ vuông góc với cả \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \). Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là tích có hướng của hai vectơ:
\(\vec n = \overrightarrow {AB} \times \overrightarrow {CD} \).
Lời giải chi tiết:
Tính vectơ chỉ phương của các cạnh:
\(\overrightarrow {AB} = B - A = (1 - 5,6 - 1,2 - 3) = ( - 4,5, - 1)\)
\(\overrightarrow {CD} = D - C = (4 - 5,0 - 0,6 - 4) = ( - 1,0,2)\)
Tính tích có hướng \(\vec n = \overrightarrow {AB} \times \overrightarrow {CD} \):
\(\vec n = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\{ - 4}&5&{ - 1}\\{ - 1}&0&2\end{array}} \right|\)
Tính từng bước:
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}5&{ - 1}\\0&2\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}{ - 4}&{ - 1}\\{ - 1}&2\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}{ - 4}&5\\{ - 1}&0\end{array}} \right|\)
\( = {\bf{i}}(5 \cdot 2 - ( - 1) \cdot 0) - {\bf{j}}( - 4 \cdot 2 - ( - 1) \cdot ( - 1)) + {\bf{k}}( - 4 \cdot 0 - 5 \cdot ( - 1))\)
\( = {\bf{i}}(10) - {\bf{j}}( - 8 - 1) + {\bf{k}}(5)\)
\( = (10,9,5)\)
Vậy vectơ pháp tuyến của mặt phẳng \((\alpha )\) là:
\(\vec n = (10,9,5)\)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 41 SGK Toán 12 Cùng khám phá
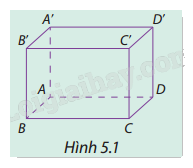
Xét các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp chữ nhật \(ABCD.A'B'C'D'\) (Hình 5.1).
a) Tìm bốn vectơ có giá trị vuông góc với mặt phẳng \((ABCD)\).
b) Tìm hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \((ABCD)\).
Phương pháp giải:
- Để tìm các vectơ vuông góc với mặt phẳng \((ABCD)\), ta tìm các vectơ có phương vuông góc với các vectơ nằm trong mặt phẳng này.
- Để tìm các vectơ nằm trong mặt phẳng \((ABCD)\), ta xét các vectơ có giá là các đoạn thẳng trong mặt phẳng đó hoặc song song với nó.
Lời giải chi tiết:
a)
- Các vectơ vuông góc với mặt phẳng \((ABCD)\) sẽ có phương vuông góc với mặt phẳng này. Các vectơ này sẽ có phương dọc theo trục\(AA',BB',CC',DD'\), vì các đoạn thẳng nối đỉnh giữa hai mặt phẳng song song \((ABCD)\) và \((A'B'C'D')\) đều vuông góc với mặt phẳng \((ABCD)\).
- Các vectơ cần tìm là:
\(\overrightarrow {AA'} ,\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \)
Đây là các vectơ có giá trị vuông góc với mặt phẳng \((ABCD)\), vì chúng có phương dọc theo chiều cao của hình hộp chữ nhật, vuông góc với mặt phẳng đáy \((ABCD)\).
b)
- Các vectơ nằm trong mặt phẳng \((ABCD)\) có phương song song với các cạnh của hình chữ nhật\(ABCD\).
- Hai vectơ không cùng phương có thể lấy như sau:
\(\overrightarrow {AB} ,\overrightarrow {AC} \)
Đây là các vectơ có giá nằm trong mặt phẳng \((ABCD)\), lần lượt dọc theo hai cạnh của hình chữ nhật\(ABCD\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 42 SGK Toán 12 Cùng khám phá
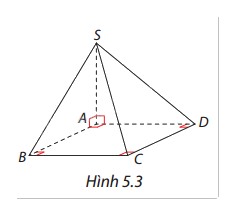
Cho hình chóp \(S.ABCD\) với \(ABCD\) là hình vuông và \(SA\) vuông góc với \((ABCD)\).
a) Tìm một vectơ pháp tuyến của các mặt phẳng \((ABCD)\), \((SAB)\), \((SAD)\), và \((SAC)\).
b) Tìm hai cặp vectơ chỉ phương của mặt phẳng \((SCD)\).
Phương pháp giải:
- Vectơ pháp tuyến của một mặt phẳng là một vectơ vuông góc với tất cả các vectơ thuộc mặt phẳng đó.
- Hai vectơ chỉ phương của một mặt phẳng là hai vectơ không đồng phương và cùng nằm trong mặt phẳng đó.
Lời giải chi tiết:
a)
- Mặt phẳng \((ABCD)\):
Theo đề bài, ta có \(SA\) vuông với mặt phẳng \((ABCD)\) nên \(\overrightarrow {SA} \) cũng là vectơ pháp tuyến của mặt phẳng \((ABCD)\).
- Mặt phẳng \((SAB)\):
Ta chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AB} \)
Theo đề bài, ta có \(DA\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AB} \) nên \(\overrightarrow {DA} \) là một vectơ pháp tuyến của mặt phẳng \((SAB)\).
- Mặt phẳng \((SAD)\):
Chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AD} \)
Theo đề bài, ta có \(BA\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AD} \) nên \(\overrightarrow {BA} \) là một vectơ pháp tuyến của mặt phẳng \((SAD)\).
- Mặt phẳng \((SAC)\):
Chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AC} \)
Theo đề bài, ta có \(BD\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AC} \) nên \(\overrightarrow {BD} \) là một vectơ pháp tuyến của mặt phẳng \((SAC)\).
b)
Các vectơ chỉ phương của mặt phẳng này là:
\(\overrightarrow {SC} ,\overrightarrow {CD} \) và \(\overrightarrow {SD} ,\overrightarrow {DC} \)
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 42 SGK Toán 12 Cùng khám phá
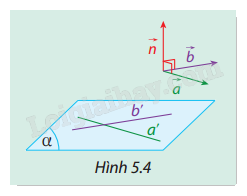
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) có cặp vectơ chỉ phương \(\vec a = ({a_1},{a_2},{a_3})\) và \(\vec b = ({b_1},{b_2},{b_3})\) (Hình 5.4). Xét vectơ \(\vec n\) được xác định như sau:
\(\vec n = ({a_2}{b_3} - {a_3}{b_2},{a_3}{b_1} - {a_1}{b_3},{a_1}{b_2} - {a_2}{b_1})\)
Tính \(\vec n \cdot \vec a\) và \(\vec n \cdot \vec b\). Vectơ \(\vec n\) có phải là một vectơ pháp tuyến của mặt phẳng \((\alpha )\) không? Vì sao?
Phương pháp giải:
Giả sử hai vectơ \(\vec a\) và \(\vec b\) có tọa độ lần lượt là:
\(\vec a = ({a_1},{a_2},{a_3}),\quad \vec b = ({b_1},{b_2},{b_3})\)
Công thức tích vô hướng của chúng là:
\(\vec a \cdot \vec b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\)
Lời giải chi tiết:
- Tính tích vô hướng \(\vec n \cdot \vec a\):
Ta có:
\(\vec n \cdot \vec a = ({a_2}{b_3} - {a_3}{b_2}){a_1} + ({a_3}{b_1} - {a_1}{b_3}){a_2} + ({a_1}{b_2} - {a_2}{b_1}){a_3}\)
Sau khi phân tích và đơn giản hóa, kết quả sẽ là \(0\).
- Tính tích vô hướng \(\vec n \cdot \vec b\):
Tương tự:
\(\vec n \cdot \vec b = ({a_2}{b_3} - {a_3}{b_2}){b_1} + ({a_3}{b_1} - {a_1}{b_3}){b_2} + ({a_1}{b_2} - {a_2}{b_1}){b_3}\)
Sau khi tính toán, kết quả cũng là \(0\).
Vì \(\vec n \cdot \vec a = 0\) và \(\vec n \cdot \vec b = 0\), vectơ \(\vec n\) vuông góc với cả \(\vec a\) và \(\vec b\). Do đó, \(\vec n\) là vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- HĐ1
- LT1
- HĐ2
- LT2
Trả lời câu hỏi Hoạt động 1 trang 41 SGK Toán 12 Cùng khám phá
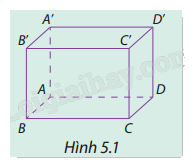
Xét các vectơ có điểm đầu và điểm cuối là hai trong tám đỉnh của hình hộp chữ nhật \(ABCD.A'B'C'D'\) (Hình 5.1).
a) Tìm bốn vectơ có giá trị vuông góc với mặt phẳng \((ABCD)\).
b) Tìm hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \((ABCD)\).
Phương pháp giải:
- Để tìm các vectơ vuông góc với mặt phẳng \((ABCD)\), ta tìm các vectơ có phương vuông góc với các vectơ nằm trong mặt phẳng này.
- Để tìm các vectơ nằm trong mặt phẳng \((ABCD)\), ta xét các vectơ có giá là các đoạn thẳng trong mặt phẳng đó hoặc song song với nó.
Lời giải chi tiết:
a)
- Các vectơ vuông góc với mặt phẳng \((ABCD)\) sẽ có phương vuông góc với mặt phẳng này. Các vectơ này sẽ có phương dọc theo trục\(AA',BB',CC',DD'\), vì các đoạn thẳng nối đỉnh giữa hai mặt phẳng song song \((ABCD)\) và \((A'B'C'D')\) đều vuông góc với mặt phẳng \((ABCD)\).
- Các vectơ cần tìm là:
\(\overrightarrow {AA'} ,\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \)
Đây là các vectơ có giá trị vuông góc với mặt phẳng \((ABCD)\), vì chúng có phương dọc theo chiều cao của hình hộp chữ nhật, vuông góc với mặt phẳng đáy \((ABCD)\).
b)
- Các vectơ nằm trong mặt phẳng \((ABCD)\) có phương song song với các cạnh của hình chữ nhật\(ABCD\).
- Hai vectơ không cùng phương có thể lấy như sau:
\(\overrightarrow {AB} ,\overrightarrow {AC} \)
Đây là các vectơ có giá nằm trong mặt phẳng \((ABCD)\), lần lượt dọc theo hai cạnh của hình chữ nhật\(ABCD\).
Trả lời câu hỏi Luyện tập 1 trang 42 SGK Toán 12 Cùng khám phá
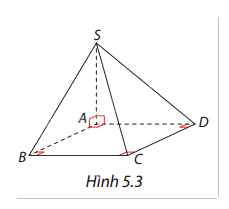
Cho hình chóp \(S.ABCD\) với \(ABCD\) là hình vuông và \(SA\) vuông góc với \((ABCD)\).
a) Tìm một vectơ pháp tuyến của các mặt phẳng \((ABCD)\), \((SAB)\), \((SAD)\), và \((SAC)\).
b) Tìm hai cặp vectơ chỉ phương của mặt phẳng \((SCD)\).
Phương pháp giải:
- Vectơ pháp tuyến của một mặt phẳng là một vectơ vuông góc với tất cả các vectơ thuộc mặt phẳng đó.
- Hai vectơ chỉ phương của một mặt phẳng là hai vectơ không đồng phương và cùng nằm trong mặt phẳng đó.
Lời giải chi tiết:
a)
- Mặt phẳng \((ABCD)\):
Theo đề bài, ta có \(SA\) vuông với mặt phẳng \((ABCD)\) nên \(\overrightarrow {SA} \) cũng là vectơ pháp tuyến của mặt phẳng \((ABCD)\).
- Mặt phẳng \((SAB)\):
Ta chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AB} \)
Theo đề bài, ta có \(DA\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AB} \) nên \(\overrightarrow {DA} \) là một vectơ pháp tuyến của mặt phẳng \((SAB)\).
- Mặt phẳng \((SAD)\):
Chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AD} \)
Theo đề bài, ta có \(BA\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AD} \) nên \(\overrightarrow {BA} \) là một vectơ pháp tuyến của mặt phẳng \((SAD)\).
- Mặt phẳng \((SAC)\):
Chọn các vectơ chỉ phương:
\(\overrightarrow {SA} ,\overrightarrow {AC} \)
Theo đề bài, ta có \(BD\) vuông góc với \(\overrightarrow {SA} ,\overrightarrow {AC} \) nên \(\overrightarrow {BD} \) là một vectơ pháp tuyến của mặt phẳng \((SAC)\).
b)
Các vectơ chỉ phương của mặt phẳng này là:
\(\overrightarrow {SC} ,\overrightarrow {CD} \) và \(\overrightarrow {SD} ,\overrightarrow {DC} \)
Trả lời câu hỏi Hoạt động 2 trang 42 SGK Toán 12 Cùng khám phá
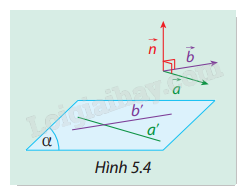
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) có cặp vectơ chỉ phương \(\vec a = ({a_1},{a_2},{a_3})\) và \(\vec b = ({b_1},{b_2},{b_3})\) (Hình 5.4). Xét vectơ \(\vec n\) được xác định như sau:
\(\vec n = ({a_2}{b_3} - {a_3}{b_2},{a_3}{b_1} - {a_1}{b_3},{a_1}{b_2} - {a_2}{b_1})\)
Tính \(\vec n \cdot \vec a\) và \(\vec n \cdot \vec b\). Vectơ \(\vec n\) có phải là một vectơ pháp tuyến của mặt phẳng \((\alpha )\) không? Vì sao?
Phương pháp giải:
Giả sử hai vectơ \(\vec a\) và \(\vec b\) có tọa độ lần lượt là:
\(\vec a = ({a_1},{a_2},{a_3}),\quad \vec b = ({b_1},{b_2},{b_3})\)
Công thức tích vô hướng của chúng là:
\(\vec a \cdot \vec b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\)
Lời giải chi tiết:
- Tính tích vô hướng \(\vec n \cdot \vec a\):
Ta có:
\(\vec n \cdot \vec a = ({a_2}{b_3} - {a_3}{b_2}){a_1} + ({a_3}{b_1} - {a_1}{b_3}){a_2} + ({a_1}{b_2} - {a_2}{b_1}){a_3}\)
Sau khi phân tích và đơn giản hóa, kết quả sẽ là \(0\).
- Tính tích vô hướng \(\vec n \cdot \vec b\):
Tương tự:
\(\vec n \cdot \vec b = ({a_2}{b_3} - {a_3}{b_2}){b_1} + ({a_3}{b_1} - {a_1}{b_3}){b_2} + ({a_1}{b_2} - {a_2}{b_1}){b_3}\)
Sau khi tính toán, kết quả cũng là \(0\).
Vì \(\vec n \cdot \vec a = 0\) và \(\vec n \cdot \vec b = 0\), vectơ \(\vec n\) vuông góc với cả \(\vec a\) và \(\vec b\). Do đó, \(\vec n\) là vectơ pháp tuyến của mặt phẳng \((\alpha )\).
Trả lời câu hỏi Luyện tập 2 trang 43 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho tứ diện \(ABCD\) có các đỉnh là \(A(5;1;3)\), \(B(1;6;2)\), \(C(5;0;4)\) và \(D(4;0;6)\). Tìm một vectơ pháp tuyến của mặt phẳng \((\alpha )\) chứa cạnh \(AB\) và song song với cạnh \(CD\).
Phương pháp giải:
Vì mặt phẳng \((\alpha )\) chứa cạnh \(AB\) và song song với cạnh \(CD\), nên vectơ pháp tuyến của mặt phẳng \((\alpha )\) sẽ vuông góc với cả \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \). Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là tích có hướng của hai vectơ:
\(\vec n = \overrightarrow {AB} \times \overrightarrow {CD} \).
Lời giải chi tiết:
Tính vectơ chỉ phương của các cạnh:
\(\overrightarrow {AB} = B - A = (1 - 5,6 - 1,2 - 3) = ( - 4,5, - 1)\)
\(\overrightarrow {CD} = D - C = (4 - 5,0 - 0,6 - 4) = ( - 1,0,2)\)
Tính tích có hướng \(\vec n = \overrightarrow {AB} \times \overrightarrow {CD} \):
\(\vec n = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\{ - 4}&5&{ - 1}\\{ - 1}&0&2\end{array}} \right|\)
Tính từng bước:
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}5&{ - 1}\\0&2\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}{ - 4}&{ - 1}\\{ - 1}&2\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}{ - 4}&5\\{ - 1}&0\end{array}} \right|\)
\( = {\bf{i}}(5 \cdot 2 - ( - 1) \cdot 0) - {\bf{j}}( - 4 \cdot 2 - ( - 1) \cdot ( - 1)) + {\bf{k}}( - 4 \cdot 0 - 5 \cdot ( - 1))\)
\( = {\bf{i}}(10) - {\bf{j}}( - 8 - 1) + {\bf{k}}(5)\)
\( = (10,9,5)\)
Vậy vectơ pháp tuyến của mặt phẳng \((\alpha )\) là:
\(\vec n = (10,9,5)\)
Giải mục 1 trang 41, 42, 43 SGK Toán 12 tập 2: Tổng quan và Phương pháp giải
Mục 1 của SGK Toán 12 tập 2 thường tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm, bao gồm các khái niệm cơ bản, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Các kiến thức trọng tâm trong Mục 1
- Đạo hàm của hàm số: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của các hàm số thường gặp: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác.
- Ứng dụng của đạo hàm: Khảo sát hàm số (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn), giải phương trình, bất phương trình.
Giải chi tiết các bài tập trang 41, 42, 43
Bài 1: (Trang 41)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Lời giải:
f'(x) = 3x2 - 4x + 5
Bài 2: (Trang 42)
Đề bài: Tìm đạo hàm của hàm số y = sin(2x).
Lời giải:
y' = 2cos(2x)
Bài 3: (Trang 43)
Đề bài: Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải:
- Xác định tập xác định: Tập xác định của hàm số là R.
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x.
- Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 và x = 2.
- Lập bảng biến thiên: Dựa vào dấu của y', ta xác định khoảng đồng biến, nghịch biến và cực trị của hàm số.
- Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Mẹo giải nhanh các bài tập về đạo hàm
Để giải nhanh các bài tập về đạo hàm, các em cần nắm vững các quy tắc tính đạo hàm cơ bản và luyện tập thường xuyên. Ngoài ra, các em có thể sử dụng các công cụ hỗ trợ tính đạo hàm trực tuyến để kiểm tra kết quả của mình.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn tự hào là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập Toán 12. Chúng tôi luôn cập nhật nội dung mới nhất và đa dạng các dạng bài tập để đáp ứng nhu cầu học tập của các em. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Bài tập | Trang | Lời giải |
|---|---|---|
| Bài 1 | 41 | f'(x) = 3x2 - 4x + 5 |
| Bài 2 | 42 | y' = 2cos(2x) |
| Bài 3 | 43 | Khảo sát hàm số y = x3 - 3x2 + 2 |