Giải mục 1 trang 10,11,12 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 10, 11, 12 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 10, 11, 12 SGK Toán 12 tập 1. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 1 của chương trình Toán 12 tập 1 thường xoay quanh các kiến thức cơ bản về hàm số, đạo hàm và ứng dụng của đạo hàm. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương tiếp theo.
Định nghĩa
LT1
Trả lời câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá
Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)
Phương pháp giải:
Bước 1: Tính\(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)
Lời giải chi tiết:
Ta có: \(f'(x) = 3{x^2} - 12x + 9\)
Xét \(f'(x) = 0\)
\( \Rightarrow 3{x^2} - 12x + 9 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Ta có bảng biến thiên là
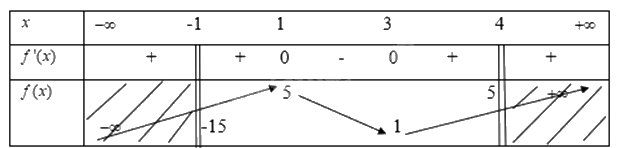
Từ bảng biến thiên ta thấy
Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)
Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x = - 1\) khi đó \(y = - 15\)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá
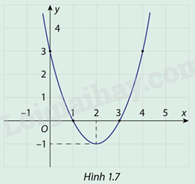
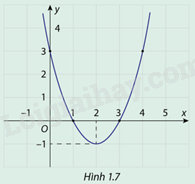
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho
b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất
b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất
Lời giải chi tiết:
a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)
b) Ta có: \(y' = 2x - 4\)
Xét \(y' = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)
Ta có bảng biến thiên
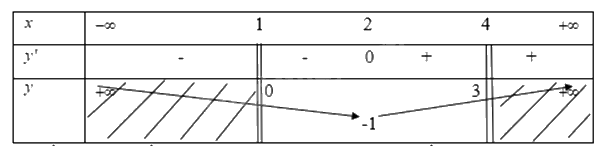
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất
LT2
Trả lời câu hỏi Luyện tập 2 trang 12 SGK Toán 12 Cùng khám phá
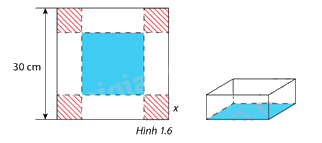
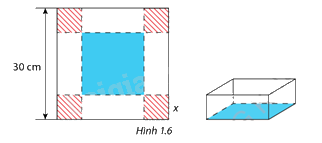
Trong một trò chơi, mỗi đội được phát một tấm bìa hình vuông có cạnh bằng 30 cm. Nhiệm vụ của mỗi đội chơi là cắt ở 4 góc của tấm bìa này 4 hình vuông bằng nhau rồi gập tấm bìa lại( hình 1.6) và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật. Đội nào thiết kế được cái hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của các hình vuông bị cắt để thu được hộp có thể tích lớn nhất.
Phương pháp giải:
Bước 1: Lập công thức tính thể tích hình hộp dước dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính thể tích lớn nhất của hình hộp là tìm giá trị lớn nhât của hàm số
Lời giải chi tiết:
Gọi độ dài hình vuông cần cắt là \(x(cm,0 < x < 30)\)
Khi đó độ dài cạnh hình hộp là\(30 - 2x\)(>0)
Thể tích hình hộp là
\(V = x(30 - 2x)(30 - 2x)\)
\( = 4{x^3} - 120{x^2} + 900x\)
Ta có \(V' = 12{x^2} - 240x + 900\)
Xét \(V' = 0\)
\( \Rightarrow 12{x^2} - 240x + 900 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 5\\x = 15\end{array} \right.\)
Ta có bảng biến thiên
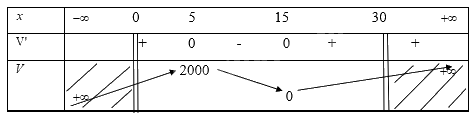
Từ bảng biến thiên ta thấy với \(x = 5\) thì thể tích hình hộp đạt giá trị lớn nhất là 2000
- HĐ1
- LT1
- LT2
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho
b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất
Phương pháp giải:
a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất
b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất
Lời giải chi tiết:
a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)
b) Ta có: \(y' = 2x - 4\)
Xét \(y' = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)
Ta có bảng biến thiên
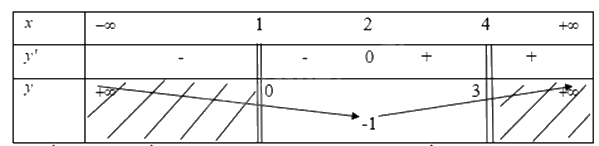
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất
Trả lời câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá
Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)
Phương pháp giải:
Bước 1: Tính\(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)
Lời giải chi tiết:
Ta có: \(f'(x) = 3{x^2} - 12x + 9\)
Xét \(f'(x) = 0\)
\( \Rightarrow 3{x^2} - 12x + 9 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Ta có bảng biến thiên là
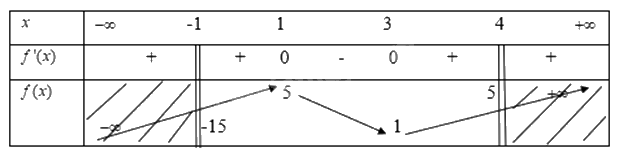
Từ bảng biến thiên ta thấy
Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)
Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x = - 1\) khi đó \(y = - 15\)
Trả lời câu hỏi Luyện tập 2 trang 12 SGK Toán 12 Cùng khám phá
Trong một trò chơi, mỗi đội được phát một tấm bìa hình vuông có cạnh bằng 30 cm. Nhiệm vụ của mỗi đội chơi là cắt ở 4 góc của tấm bìa này 4 hình vuông bằng nhau rồi gập tấm bìa lại( hình 1.6) và dán keo để được một cái hộp không nắp có dạng hình hộp chữ nhật. Đội nào thiết kế được cái hộp có thể tích lớn nhất sẽ dành chiến thắng. Hãy xác định cạnh của các hình vuông bị cắt để thu được hộp có thể tích lớn nhất.
Phương pháp giải:
Bước 1: Lập công thức tính thể tích hình hộp dước dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính thể tích lớn nhất của hình hộp là tìm giá trị lớn nhât của hàm số
Lời giải chi tiết:
Gọi độ dài hình vuông cần cắt là \(x(cm,0 < x < 30)\)
Khi đó độ dài cạnh hình hộp là\(30 - 2x\)(>0)
Thể tích hình hộp là
\(V = x(30 - 2x)(30 - 2x)\)
\( = 4{x^3} - 120{x^2} + 900x\)
Ta có \(V' = 12{x^2} - 240x + 900\)
Xét \(V' = 0\)
\( \Rightarrow 12{x^2} - 240x + 900 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 5\\x = 15\end{array} \right.\)
Ta có bảng biến thiên
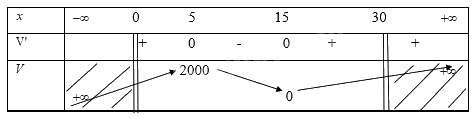
Từ bảng biến thiên ta thấy với \(x = 5\) thì thể tích hình hộp đạt giá trị lớn nhất là 2000
Giải mục 1 trang 10, 11, 12 SGK Toán 12 tập 1: Tổng quan và hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 1 tập trung vào việc ôn tập và mở rộng kiến thức về hàm số, bao gồm các loại hàm số thường gặp như hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit và các phép biến đổi hàm số. Ngoài ra, mục này cũng giới thiệu về đạo hàm, một khái niệm quan trọng trong giải tích, và các ứng dụng cơ bản của đạo hàm trong việc tìm cực trị, xét tính đơn điệu của hàm số.
Nội dung chính của mục 1 trang 10, 11, 12
- Hàm số: Định nghĩa, tập xác định, tập giá trị, tính đơn điệu, cực trị.
- Đạo hàm: Định nghĩa, ý nghĩa hình học, các quy tắc tính đạo hàm.
- Ứng dụng của đạo hàm: Tìm cực trị, xét tính đơn điệu, giải phương trình, bất phương trình.
Hướng dẫn giải chi tiết các bài tập trong mục 1
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1, tusach.vn xin giới thiệu một số bài tập tiêu biểu và hướng dẫn giải chi tiết:
Bài 1: Tìm tập xác định của hàm số
Để tìm tập xác định của hàm số, các em cần xác định các giá trị của x sao cho biểu thức của hàm số có nghĩa. Ví dụ, với hàm số y = √(x-2), tập xác định là x ≥ 2.
Bài 2: Tính đạo hàm của hàm số
Để tính đạo hàm của hàm số, các em cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, đạo hàm của hàm số y = x2 là y' = 2x.
Bài 3: Tìm cực trị của hàm số
Để tìm cực trị của hàm số, các em cần giải phương trình đạo hàm bằng 0 và xét dấu đạo hàm để xác định các điểm cực trị. Ví dụ, với hàm số y = x3 - 3x2 + 2, đạo hàm là y' = 3x2 - 6x. Giải phương trình y' = 0, ta được x = 0 và x = 2. Xét dấu đạo hàm, ta thấy x = 0 là điểm cực đại và x = 2 là điểm cực tiểu.
Mẹo học tập hiệu quả
- Nắm vững định nghĩa và các khái niệm cơ bản: Đây là nền tảng quan trọng để hiểu và giải các bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp các em rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Sách giáo khoa, sách bài tập, các trang web học tập trực tuyến là những nguồn tài liệu hữu ích.
- Hỏi thầy cô giáo hoặc bạn bè: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè để được giúp đỡ.
Bảng tổng hợp các công thức đạo hàm thường gặp
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
Tusach.vn hy vọng với những hướng dẫn chi tiết và hữu ích trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 10, 11, 12 SGK Toán 12 tập 1. Chúc các em học tập tốt!