Giải Bài Tập 1.23 Trang 35 SGK Toán 12 Tập 1

Giải bài tập 1.23 trang 35 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.23 trang 35 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và đầy đủ nhất.

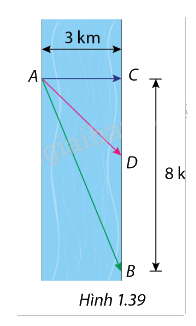
Một người chèo thuyền từ điểm A trên bờ một con sông thẳng, rộng 3 km và muốn đến điểm B, cách bờ đối diện 8 km về phía hạ lưu, càng nhanh càng tốt như Hình 1.39. Người ấy có thể chèo thuyền qua sông đến điểm C rồi chạy bộ đến B, hoặc anh ta có thể chèo thuyền đến D nào đó giữa C và B rồi chạy bộ đến B. Tốc độ chèo thuyền là 6 km/h và tốc độ chạy bộ là 8 km/h. Tìm thời gian ngắn nhất mà người này có thể đi từ A đến B (bỏ qua vận tốc của nước và làm tròn kết quả đến hàng phần trăm).

Đề bài

Một người chèo thuyền từ điểm A trên bờ một con sông thẳng, rộng 3 km và muốn đến điểm B, cách bờ đối diện 8 km về phía hạ lưu, càng nhanh càng tốt như Hình 1.39. Người ấy có thể chèo thuyền qua sông đến điểm C rồi chạy bộ đến B, hoặc anh ta có thể chèo thuyền đến D nào đó giữa C và B rồi chạy bộ đến B. Tốc độ chèo thuyền là 6 km/h và tốc độ chạy bộ là 8 km/h. Tìm thời gian ngắn nhất mà người này có thể đi từ A đến B (bỏ qua vận tốc của nước và làm tròn kết quả đến hàng phần trăm).

Giải bài tập 1.23 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 1.23 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 2

- Đặt biến 𝑥 là khoảng cách từ điểm C đến điểm D.

- Thiết lập hàm số 𝑇(𝑥) thời gian tổng quát bao gồm thời gian chèo thuyền và thời gian chạy bộ.

- Khảo sát hàm số 𝑇(𝑥).

- Tính thời gian tại giá trị 𝑥 tìm được để đảm bảo đó là thời gian ngắn nhất.

Lời giải chi tiết

- Gọi 𝑥 là khoảng cách từ điểm C đến điểm D (BC≥𝑥≥0).

- Quãng đường từ A đến D là: \(\sqrt {{3^2} + {x^2}} = \sqrt {9 + {x^2}} \)km.

- Thời gian chèo thuyền là: \(\frac{{\sqrt {9 + {x^2}} }}{6}\) giờ.

- Thời gian chạy bộ từ D đến B là:\(\frac{{8 - x}}{8}\) giờ.

→ Tổng thời gian: \[T(x) = \frac{{\sqrt {9 + {x^2}} }}{6} + \frac{{8 - x}}{8}\]

- Khảo sát hàm số 𝑇(𝑥):

Tính đạo hàm: \({T^\prime }(x) = \frac{1}{6} \cdot \frac{x}{{\sqrt {9 + {x^2}} }} - \frac{1}{8}\)

Giải phương trình \({T^\prime }(x) = 0\) :

\(\begin{array}{l}\frac{x}{{6\sqrt {9 + {x^2}} }} = \frac{1}{8}\\ \Rightarrow 8x = 6\sqrt {9 + {x^2}} \\ \Leftrightarrow 64{x^2} = 36\left( {9 + {x^2}} \right)\\ \Leftrightarrow 64{x^2} = 324 + 36{x^2}\\ \Leftrightarrow 28{x^2} = 324\\ \Rightarrow x = \sqrt {\frac{{324}}{{28}}} = \frac{{924}}{{\sqrt 7 }} \approx 3.4\end{array}\)

Bảng biến thiên:

Giải bài tập 1.23 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 3

Thời gian ngắn nhất mà người này có thể đi từ A đến B là 1.33 giờ.

Giải Bài Tập 1.23 Trang 35 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 1.23 trang 35 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

Đề Bài Bài Tập 1.23 Trang 35 SGK Toán 12 Tập 1

(Đề bài cụ thể của bài tập 1.23 sẽ được chèn vào đây. Ví dụ: Khảo sát hàm số y = x³ - 3x² + 2)

Phương Pháp Giải

Tính đạo hàm cấp nhất (y'): Tìm đạo hàm của hàm số đã cho.
Tìm điểm dừng: Giải phương trình y' = 0 để tìm các điểm mà tại đó đạo hàm bằng không.
Lập bảng biến thiên: Xác định dấu của y' trên các khoảng xác định bởi các điểm dừng. Từ đó, xác định khoảng đồng biến, nghịch biến của hàm số.
Xác định cực trị: Sử dụng dấu của y' để xác định các điểm cực đại, cực tiểu của hàm số.
Tính đạo hàm cấp hai (y''): Tìm đạo hàm cấp hai của hàm số.
Xác định điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn của hàm số.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập được, vẽ đồ thị hàm số.

Lời Giải Chi Tiết Bài Tập 1.23 Trang 35 SGK Toán 12 Tập 1

(Lời giải chi tiết, từng bước của bài tập 1.23 sẽ được trình bày ở đây. Bao gồm các bước tính đạo hàm, tìm điểm dừng, lập bảng biến thiên, xác định cực trị, tính đạo hàm cấp hai, xác định điểm uốn và vẽ đồ thị hàm số.)

Ví Dụ Minh Họa

Để giúp các em hiểu rõ hơn về phương pháp giải, chúng ta sẽ xét một ví dụ cụ thể:

(Ví dụ minh họa với một hàm số tương tự, giải chi tiết từng bước.)

Lưu Ý Quan Trọng

Luôn kiểm tra lại các phép tính đạo hàm để đảm bảo tính chính xác.
Chú ý đến tập xác định của hàm số.
Sử dụng đồ thị hàm số để kiểm tra lại kết quả.

Bài Tập Tương Tự

Để rèn luyện thêm kỹ năng giải bài tập về khảo sát hàm số, các em có thể tham khảo các bài tập tương tự sau:

Bài tập 1.24 trang 35 SGK Toán 12 tập 1
Bài tập 1.25 trang 36 SGK Toán 12 tập 1

Kết Luận

Bài tập 1.23 trang 35 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với lời giải chi tiết và dễ hiểu này, các em sẽ tự tin hơn trong quá trình học tập.

Tusach.vn luôn sẵn sàng hỗ trợ các em trong mọi vấn đề học tập. Chúc các em học tốt!