Giải bài tập 1.31 trang 45 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.31 Trang 45 SGK Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.31 trang 45 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
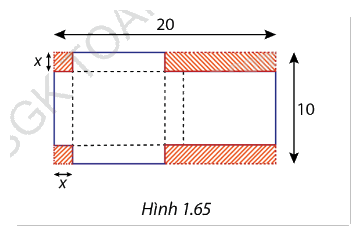
Từ một miếng bìa hình chữ nhật với kích thước 20cm x 10cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc Hình 1.65) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Tìm x để thể tích hộp là lớn nhất và tính giá trị lớn nhất đó.
Đề bài
Từ một miếng bìa hình chữ nhật với kích thước 20cm x 10cm, bạn Lan cắt bỏ hai hình vuông có cạnh là x (cm) và hai hình chữ nhật (phần gạch sọc Hình 1.65) rồi gấp theo đường nét đứt và dán các mép để được một cái hộp có dạng hình hộp chữ nhật. Tìm x để thể tích hộp là lớn nhất và tính giá trị lớn nhất đó.
Phương pháp giải - Xem chi tiết
- Xác định chiều dài, chiều rộng và chiều cao của hộp sau khi cắt bỏ hình vuông và hình chữ nhật.
- Tìm công thức của hộp dựa trên các kích thước đã được xác định.
- Khảo sát hàm số thể tích để tìm giá trị lớn nhất.
Lời giải chi tiết
- Sau khi cắt bỏ và gấp lại, các phần còn lại của miếng bìa sẽ tạo thành một hình hộp chữ nhật kích thước:
Chiều dài: \(\frac{{20}}{2} - x = 10 - x\) (cm)
Chiều rộng: 10−2𝑥 (cm)
Chiều cao: 𝑥 (cm)
- Thể tích của hình hộp chữ nhật là:
\(\begin{array}{l}V = x.(10 - x).(10 - 2x)\\ = (10x - {x^2}).(10 - 2x)\\ = 2{x^3} - 30{x^2} + 100x\end{array}\)
- Đạo hàm của hàm số thể tích là: \(V'(x) = 6{x^2} - 60x + 100\)
- Giải phương trình \(V'(x) = 0\):
\(6{x^2} - 60x + 100 = 0 \Leftrightarrow 3{x^2} - 30x + 50 = 0 \Rightarrow x = 5 \pm \frac{{5\sqrt 3 }}{5}\)
Vì miền xác định của 𝑥 là \(0 \le x \le 5\)nên chỉ nhận giá trị \(x = 5 - \frac{{5\sqrt 3 }}{5}\)
- Bảng biến thiên:
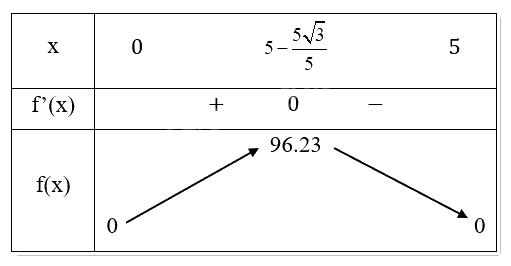
Vậy \(x = 5 - \frac{{5\sqrt 3 }}{5} \approx 2,11\) thì thể tích hình hộp là lớn nhất và có giá trị là \({V_{\max }} \approx 96.23\)cm3.
Giải Bài Tập 1.31 Trang 45 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu
Bài tập 1.31 trang 45 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề Bài Bài Tập 1.31 Trang 45 SGK Toán 12 Tập 1
Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và tìm các điểm cực trị.
Lời Giải Chi Tiết
- Xác định tập xác định của hàm số: Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
- Tính đạo hàm cấp nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được: 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2. Vậy, các điểm dừng của hàm số là x1 = 0 và x2 = 2.
- Xác định dấu của đạo hàm cấp nhất:
- Với x < 0, y' > 0, hàm số đồng biến.
- Với 0 < x < 2, y' < 0, hàm số nghịch biến.
- Với x > 2, y' > 0, hàm số đồng biến.
- Kết luận về cực trị:
- Tại x = 0, y' đổi dấu từ dương sang âm, hàm số đạt cực đại và giá trị cực đại là yCĐ = 03 - 3(0)2 + 2 = 2.
- Tại x = 2, y' đổi dấu từ âm sang dương, hàm số đạt cực tiểu và giá trị cực tiểu là yCT = 23 - 3(2)2 + 2 = 8 - 12 + 2 = -2.
Bảng Biến Thiên
| x | -∞ | 0 | 2 | +∞ | |
|---|---|---|---|---|---|
| y' | + | 0 | - | 0 | + |
| y | ↗ | 2 (CĐ) | ↘ | -2 (CT) | ↗ |
Nhận Xét và Mở Rộng
Bài tập này là một ví dụ điển hình về việc khảo sát hàm số bằng đạo hàm. Việc nắm vững các bước thực hiện và hiểu rõ ý nghĩa của đạo hàm sẽ giúp các em giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.
Ngoài ra, các em có thể tìm hiểu thêm về các ứng dụng khác của đạo hàm trong việc giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc xác định khoảng đồng biến, nghịch biến của hàm số.
Tusach.vn – Đồng Hành Cùng Các Em
Tusach.vn luôn cập nhật những lời giải bài tập mới nhất và chính xác nhất. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập môn Toán 12!