Giải bài tập 5.42 trang 85 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 5.42 Trang 85 Toán 12 Tập 2
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5.42 trang 85 SGK Toán 12 tập 2. Bài tập này thuộc chương trình học về số phức và các phép toán liên quan.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp kiến thức chính xác và dễ hiểu nhất.
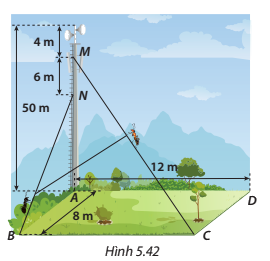
Một tháp phát sóng cao 50 m đặt ở góc A của sân hình chữ nhật ABCD. Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp CM và BN (từ C và B) với vận tốc lần lượt là 3 m/phút và 2,5 m/phút. Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Đề bài
Một tháp phát sóng cao 50 m đặt ở góc A của sân hình chữ nhật ABCD. Để giữ cho tháp không bị đổ, người ta có cột rất nhiều dây cáp quanh tháp và cố định tại các vị trí trên mặt đất. Hai chú kiến vàng và kiến đen bắt đầu leo lên hai dây cáp CM và BN (từ C và B) với vận tốc lần lượt là 3 m/phút và 2,5 m/phút. Hỏi sau 10 phút thì hai chú kiến cách nhau bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
- Xác định các điểm mà các chú kiến bắt đầu leo lên dây và điểm đến trên cột.
- Tính chiều dài của các đoạn dây (ví dụ: CM và BN) dựa trên vị trí các điểm gốc của dây.
- Dựa vào vận tốc của mỗi chú kiến, tính toán quãng đường mà mỗi chú kiến leo được sau thời gian đã cho.
- Sử dụng tọa độ của hai chú kiến sau thời gian leo lên để xác định khoảng cách giữa chúng, có thể sử dụng công thức khoảng cách giữa hai điểm trong không gian.
Lời giải chi tiết
* Đặt gốc toạ độ tại A, trục Ox chứa cạnh AB, trục Oy chứa cạnh AD và trục Oz chứa cạnh AM
- Toạ độ các điểm là: \(A(0;0;0)\), \(B(8;0;0)\), \(D(0;12;0)\), \(C(8;12;0)\), \(M(0;0;46)\), \(N(0;0;40)\).
* Tính chiều dài của dây cáp CM và BN:
- Dây cáp \(\overrightarrow {CM} ( - 8; - 12;46)\): \(CM = \sqrt {{{(0 - 8)}^2} + {{(0 - 12)}^2} + {{(46 - 0)}^2}} = 2\sqrt {581} \approx 48,2{\mkern 1mu} {\rm{m}}\)
- Dây cáp \(\overrightarrow {BN} ( - 8;0;40)\): \(BN = \sqrt {{{(0 - 8)}^2} + {{(40 - 0)}^2}} = 8\sqrt {26} \approx 40,8{\mkern 1mu} {\rm{m}}\)
* Tính quãng đường hai chú kiến leo lên sau 10 phút:
- Quãng đường chú kiến vàng leo lên dây CM: \({S_{CM}} = 3 \times 10 = 30{\mkern 1mu} {\rm{m}}\)
- Quãng đường chú kiến đen leo lên dây BN: \({S_{BN}} = 2.5 \times 10 = 25{\mkern 1mu} {\rm{m}}\)
* Xác định vị trí của hai chú kiến trên các dây cáp CM và BN sau 10 phút:
- Tỉ lệ vị trí của chú kiến vàng trên dây CM: \(\frac{{{S_{CM}}}}{{CM}} = \frac{{30}}{{48,2}} \approx 0,62\)
- Tọa độ của chú kiến vàng sau 10 phút là:
\(({x_{M'}},{y_{M'}},{z_{M'}}) = 0.62 \times \overrightarrow {CM} + C = (0,62 \times ( - 8);0,62 \times ( - 12);0,62 \times 46) + (8;12;0) \approx (3,04;4,56;28,52)\)
- Tỉ lệ vị trí của chú kiến đen trên dây BN: \(\frac{{{S_{BN}}}}{{BN}} = \frac{{25}}{{40,8}} \approx 0,61\)
- Tọa độ của chú kiến đen sau 10 phút là:
\(({x_{N'}},{y_{N'}},{z_{N'}}) = 0,61 \times \overrightarrow {BN} + \overrightarrow B = (0,61 \times ( - 8);0;0,61 \times 40) + (8;0;0) \approx (3,12;0;24,4)\)
* Tính khoảng cách giữa hai chú kiến Khoảng cách giữa hai chú kiến là:
\(d = \sqrt {{{({x_{M'}} - {x_{N'}})}^2} + {{({y_{M'}} - {y_{N'}})}^2} + {{({z_{M'}} - {z_{N'}})}^2}} \)
Thay các giá trị vào:
\(d = \sqrt {{{(3,04 - 3,12)}^2} + {{(4,56 - 0)}^2} + {{(28,52 - 24,4)}^2}} \approx 6,15\)
Vậy sau 10 phút, khoảng cách giữa hai chú kiến là khoảng 6,15 m (làm tròn đến hàng phần trăm).
Giải Bài Tập 5.42 Trang 85 Toán 12 Tập 2: Hướng Dẫn Chi Tiết
Bài tập 5.42 trang 85 SGK Toán 12 tập 2 yêu cầu chúng ta tìm số phức z thỏa mãn một điều kiện nhất định. Để giải bài tập này, chúng ta cần nắm vững kiến thức về số phức, bao gồm dạng đại số của số phức, các phép toán cộng, trừ, nhân, chia số phức, và đặc biệt là module của số phức.
Đề Bài Bài Tập 5.42 Trang 85 Toán 12 Tập 2
(Đề bài cụ thể của bài tập 5.42 sẽ được chèn vào đây. Ví dụ: Tìm số phức z biết |z - 1| = |z + i| và z.z̅ = 5)
Phương Pháp Giải Bài Tập Về Số Phức
Để giải quyết bài toán này, chúng ta có thể áp dụng các phương pháp sau:
- Biểu diễn số phức trên mặt phẳng phức: Sử dụng mặt phẳng phức để hình dung các điều kiện của bài toán. Ví dụ, |z - a| = r biểu diễn một đường tròn tâm a bán kính r.
- Sử dụng các tính chất của module số phức: |z1 + z2| ≤ |z1| + |z2|, |z1 - z2| ≥ ||z1| - |z2||.
- Đặt z = x + yi: Thay z = x + yi vào phương trình và sử dụng các phép toán đại số để tìm x và y.
- Sử dụng z.z̅ = x2 + y2: Công thức này giúp liên hệ giữa số phức và tọa độ của nó trên mặt phẳng phức.
Lời Giải Chi Tiết Bài Tập 5.42 Trang 85 Toán 12 Tập 2
(Lời giải chi tiết, từng bước của bài tập 5.42 sẽ được trình bày ở đây. Bao gồm các bước đặt z = x + yi, thay vào phương trình, biến đổi đại số, tìm ra x và y, và kết luận nghiệm của z.)
Ví dụ, nếu đề bài là: Tìm số phức z biết |z - 1| = |z + i| và z.z̅ = 5
Giải:
- Đặt z = x + yi (x, y ∈ ℝ)
- |z - 1| = |z + i| ⇔ |(x - 1) + yi| = |x + (y + 1)i| ⇔ (x - 1)2 + y2 = x2 + (y + 1)2 ⇔ x2 - 2x + 1 + y2 = x2 + y2 + 2y + 1 ⇔ -2x = 2y ⇔ x = -y
- z.z̅ = 5 ⇔ (x + yi)(x - yi) = 5 ⇔ x2 + y2 = 5
- Thay x = -y vào x2 + y2 = 5, ta được (-y)2 + y2 = 5 ⇔ 2y2 = 5 ⇔ y2 = 5/2 ⇔ y = ±√(5/2)
- Khi y = √(5/2) thì x = -√(5/2). Khi y = -√(5/2) thì x = √(5/2)
- Vậy z = -√(5/2) + √(5/2)i hoặc z = √(5/2) - √(5/2)i
Lưu Ý Khi Giải Bài Tập Về Số Phức
- Luôn kiểm tra lại kết quả bằng cách thay nghiệm tìm được vào phương trình ban đầu.
- Sử dụng các công thức và tính chất của số phức một cách chính xác.
- Rèn luyện kỹ năng biến đổi đại số để giải quyết các phương trình liên quan đến số phức.
Tổng Kết
Bài tập 5.42 trang 85 SGK Toán 12 tập 2 là một bài tập điển hình về ứng dụng của số phức trong giải toán. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh có thể tự tin giải quyết các bài tập tương tự.
Mọi thắc mắc hoặc cần hỗ trợ thêm, đừng ngần ngại liên hệ với tusach.vn. Chúc các em học tập tốt!