Giải mục 1 trang 67, 68 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 67, 68 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 67, 68 sách giáo khoa Toán 12 tập 2. Bài viết này của tusach.vn sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh.
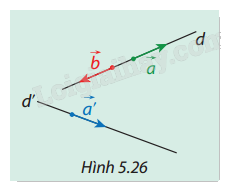
Cho hai vectơ ngược hướng (vec a) và (vec b) là hai vectơ chỉ phương của đường thẳng (d) và (vec a') là vectơ chỉ phương của đường thẳng (d')(Hình 5.26). Cho biết ((d,d') = {45^{^circ }}). Hãy tính số đo của hai góc: (left( {vec a,vec a'} right)) và ((vec b,vec a')). Từ đó chỉ ra mối quan hệ giữa hai góc ((d,d')) và ((vec a,vec a')), giữa (cos (d,d')) và (cos (vec a,vec a')).
LT1
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau:
a) \(d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và \(d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}\)
b) \(d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}\) và \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.\) \((t \in \mathbb{R})\)
Phương pháp giải:
Xác định vector chỉ phương của mỗi đường thẳng.
Sử dụng công thức cosin góc giữa hai vector: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}}\).
Tính góc từ giá trị cosin.
Lời giải chi tiết:
a)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (3,4,5)\)
\(d':\overrightarrow {{a_2}} = (4,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{3 \cdot 4 + 4 \cdot 2 + 5 \cdot 2}}{{\sqrt {({3^2} + {4^2} + {5^2})({4^2} + {2^2} + {2^2})} }}\)
\( = \frac{{12 + 8 + 10}}{{\sqrt {(9 + 16 + 25)(16 + 4 + 4)} }}\)
\( = \frac{{30}}{{\sqrt {50 \cdot 24} }}\)
\( = \frac{3}{{\sqrt 2 }}\)
Suy ra góc \(\phi = 30^\circ \)
b)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (2, - 4,5)\)
\(d':\overrightarrow {{a_2}} = ( - 1,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{2 \cdot ( - 1) + ( - 4) \cdot 2 + 5 \cdot 2}}{{\sqrt {({2^2} + {{( - 4)}^2} + {5^2})({{( - 1)}^2} + {2^2} + {2^2})} }}\)
\( = \frac{{ - 2 - 8 + 10}}{{\sqrt {(4 + 16 + 25)(1 + 4 + 4)} }}\)
\( = \frac{0}{{\sqrt {45 \cdot 9} }}\)
\( = 0\)
Do \(\cos (\phi ) = 0\), nên \(\phi = 90^\circ \)
- HĐ1
- LT1
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 12 Cùng khám phá
Cho hai vectơ ngược hướng \(\vec a\) và \(\vec b\) là hai vectơ chỉ phương của đường thẳng \(d\) và \(\vec a'\) là vectơ chỉ phương của đường thẳng \(d'\)(Hình 5.26). Cho biết \((d,d') = {45^{^\circ }}\). Hãy tính số đo của hai góc: \(\left( {\vec a,\vec a'} \right)\) và \((\vec b,\vec a')\). Từ đó chỉ ra mối quan hệ giữa hai góc \((d,d')\) và \((\vec a,\vec a')\), giữa \(\cos (d,d')\) và \(\cos (\vec a,\vec a')\).
Phương pháp giải:
Sử dụng tích vô hướng của hai vectơ để tính góc giữa chúng:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
Lời giải chi tiết:
- Góc giữa \(\vec a\) và \(\vec a'\):
Ta sử dụng công thức cosin cho góc giữa hai vectơ:
\(\cos (\vec a,\vec a') = \frac{{\vec a \cdot \vec a'}}{{\left| {\vec a} \right|.\left| {\vec a'} \right|}} = \frac{{{a_1}{{a'}_1} + {a_2}{{a'}_2} + {a_3}{{a'}_3}}}{{\sqrt {(a_1^2 + a_2^2 + a_3^2)({a_1}{'^2} + {a_2}{'^2} + {a_3}{'^2})} }}\)
Biết rằng \((d,d') = {45^\circ }\) và Vì \(\overrightarrow a \) là vector chỉ phương của d và \(\overrightarrow {a'} \) là vector chỉ phương của d' nên góc giữa hai vector bằng góc giữa hai đường thẳng. Suy ra góc giữa \(\vec a\) và \(\vec a'\) là \({45^\circ }\).
- Góc giữa \(\vec b\) và \(\vec a'\):
Vì \(\vec b = - \vec a\), ta có:
\(\cos \left( {\vec b,\vec a'} \right) = \cos \left( { - \vec a,\vec a'} \right) = - \cos \left( {\vec a,\vec a'} \right) = - \cos 45^\circ \)
Suy ra:
\(\cos \left( {\vec b,\vec a'} \right) = - \frac{1}{{\sqrt 2 }}\)
Do đó, góc giữa \(\vec b\) và \(\vec a'\) là \({135^\circ }\).
- Mối quan hệ giữa hai góc:
Góc giữa hai đường thẳng \((d,d')\) và góc giữa hai vectơ chỉ phương \(\vec a\) và \(\vec a'\) bằng nhau, tức là: \((d,d') = \left( {\vec a,\vec a'} \right) = {45^\circ }\)
- Tương tự, mối quan hệ giữa \(\cos (d,d')\) và \(\cos \left( {\vec a,\vec a'} \right)\) là: \(\cos (d,d') = \cos \left( {\vec a,\vec a'} \right) = \frac{1}{{\sqrt 2 }}\)
Trả lời câu hỏi Luyện tập 1 trang 68 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa hai đường thẳng d và d' trong các trường hợp sau:
a) \(d:\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và \(d':\frac{{x - 1}}{4} = \frac{y}{2} = \frac{{z + 1}}{2}\)
b) \(d:\frac{x}{2} = \frac{y}{{ - 4}} = \frac{z}{5}\) và \(d':\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}x = 2 - t\;\\y = 3 + 2t\;\\z = 2t\end{array}\end{array}} \right.\) \((t \in \mathbb{R})\)
Phương pháp giải:
Xác định vector chỉ phương của mỗi đường thẳng.
Sử dụng công thức cosin góc giữa hai vector: \(\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}}\).
Tính góc từ giá trị cosin.
Lời giải chi tiết:
a)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (3,4,5)\)
\(d':\overrightarrow {{a_2}} = (4,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{3 \cdot 4 + 4 \cdot 2 + 5 \cdot 2}}{{\sqrt {({3^2} + {4^2} + {5^2})({4^2} + {2^2} + {2^2})} }}\)
\( = \frac{{12 + 8 + 10}}{{\sqrt {(9 + 16 + 25)(16 + 4 + 4)} }}\)
\( = \frac{{30}}{{\sqrt {50 \cdot 24} }}\)
\( = \frac{3}{{\sqrt 2 }}\)
Suy ra góc \(\phi = 30^\circ \)
b)
Vector chỉ phương:
\(d:\overrightarrow {{a_1}} = (2, - 4,5)\)
\(d':\overrightarrow {{a_2}} = ( - 1,2,2)\)
Áp dụng công thức:
\(\cos (\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} ) = \frac{{2 \cdot ( - 1) + ( - 4) \cdot 2 + 5 \cdot 2}}{{\sqrt {({2^2} + {{( - 4)}^2} + {5^2})({{( - 1)}^2} + {2^2} + {2^2})} }}\)
\( = \frac{{ - 2 - 8 + 10}}{{\sqrt {(4 + 16 + 25)(1 + 4 + 4)} }}\)
\( = \frac{0}{{\sqrt {45 \cdot 9} }}\)
\( = 0\)
Do \(\cos (\phi ) = 0\), nên \(\phi = 90^\circ \)
Giải mục 1 trang 67, 68 SGK Toán 12 tập 2: Tổng quan và Phương pháp giải
Mục 1 trang 67, 68 SGK Toán 12 tập 2 thường xoay quanh các chủ đề về Đạo hàm của hàm số lượng giác hoặc Ứng dụng của đạo hàm để khảo sát hàm số. Để giải tốt các bài tập trong mục này, học sinh cần nắm vững các kiến thức cơ bản sau:
- Các công thức đạo hàm cơ bản của hàm số lượng giác: (sin x)' = cos x, (cos x)' = -sin x, (tan x)' = 1/cos2x, (cot x)' = -1/sin2x
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Ứng dụng của đạo hàm: Tìm cực trị, khoảng đơn điệu, điểm uốn của hàm số.
Giải chi tiết các bài tập trong mục 1 trang 67, 68
Bài 1: (Ví dụ minh họa)
Cho hàm số y = sin2x. Tính đạo hàm y'.
Lời giải:
Áp dụng quy tắc đạo hàm hàm hợp, ta có:
y' = 2sin x * (sin x)' = 2sin x * cos x = sin 2x
Bài 2: (Ví dụ minh họa)
Tìm cực trị của hàm số y = x3 - 3x + 2.
Lời giải:
- Tính đạo hàm y' = 3x2 - 3
- Giải phương trình y' = 0 để tìm điểm cực trị: 3x2 - 3 = 0 => x = ±1
- Lập bảng biến thiên để xác định cực đại, cực tiểu:
| x | -∞ | -1 | 1 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | + |
| y | ↗ | ↘ | ↗ | ↗ |
Vậy hàm số đạt cực đại tại x = -1, ycđ = 4 và đạt cực tiểu tại x = 1, yct = 0.
Mẹo giải nhanh và hiệu quả
- Nắm vững các công thức đạo hàm: Việc thuộc lòng các công thức đạo hàm cơ bản sẽ giúp bạn tiết kiệm thời gian và tránh sai sót.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau sẽ giúp bạn hiểu rõ hơn về các dạng bài và rèn luyện kỹ năng giải toán.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong SGK Toán 12 tập 2. Chúng tôi hy vọng rằng những lời giải này sẽ giúp các em học tập tốt hơn và đạt kết quả cao trong các kỳ thi.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.