Đề bài
Hai bảng dưới đây biểu diễn kết quả đo đường kính (tính theo mm) của một số ổ bi được sản xuất bởi các máy X và Y:
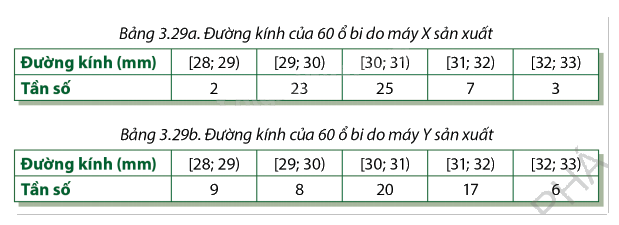
a) Ước tính giá trị trung bình và độ lệch chuẩn của đường kính các ổ bi được sản xuất bởi mỗi máy.
b) Biết rằng đường kính mong muốn cho các ổ bi là 30,4 mm. Hãy phân tích chất lượng sản phẩm do mỗi máy sản xuất.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức sau:
- Công thức tính trung bình:
\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)
b) So sánh giá trị trung bình và độ lệch chuẩn với giá trị mong muốn (30,4 mm) để đánh giá sự chính xác và độ phân tán của sản phẩm.
Lời giải chi tiết
Bảng phân phối tần số cho máy X và Y:
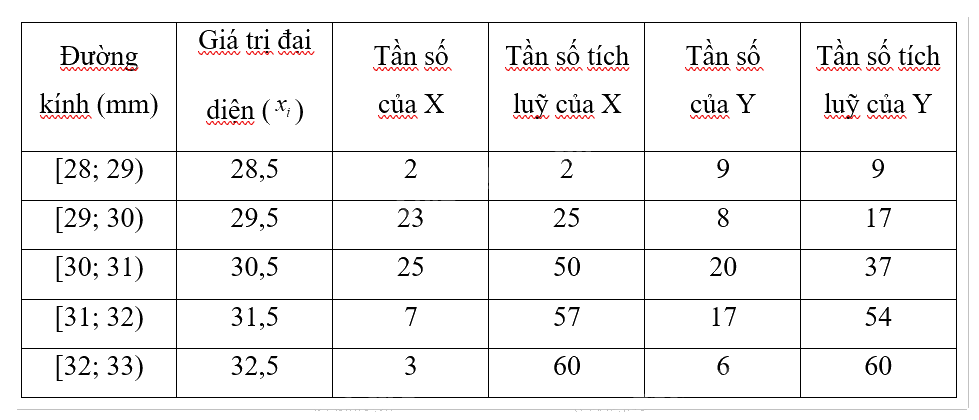
Dựa vào bảng phân phối ta thấy N = 60.
Giá trị trung bình của máy X:
\({\bar x_X} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{2 \times 28,5 + 23 \times 29,5 + 25 \times 30,5 + 7 \times 31,5 + 3 \times 32,5}}{{60}} = \frac{{1816}}{{60}} \approx 30,27\)
Độ lệch chuẩn của máy X:
\({S_X} = \sqrt {\overline {x_X^2} - {{\left( {{{\bar x}_X}} \right)}^2}} \)
\(\overline {x_X^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{2 \times 28,{5^2} + 23 \times 29,{5^2} + 25 \times 30,{5^2} + 7 \times 31,{5^2} + 3 \times 32,{5^2}}}{{60}} = \frac{{55011}}{{60}} = 916,85\)
\({S_X} = \sqrt {916,85 - 30,{{27}^2}} = \sqrt {0,78} \approx 0,88\)
Giá trị trung bình của máy Y:
\({\bar x_Y} = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{9 \times 28,5 + 8 \times 29,5 + 20 \times 30,5 + 17 \times 31,5 + 6 \times 32,5}}{{60}} = \frac{{1833}}{{60}} = 30,55\)
Độ lệch chuẩn của phương pháp B:
\({S_Y} = \sqrt {\overline {x_Y^2} - {{\left( {{{\bar x}_Y}} \right)}^2}} \)
\(\overline {x_Y^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{9 \times 28,{5^2} + 8 \times 29,{5^2} + 20 \times 30,{5^2} + 17 \times 31,{5^2} + 6 \times 32,{5^2}}}{{60}} = \frac{{56083}}{{60}} \approx 934,72\)
\({S_Y} = \sqrt {934,72 - 30,{{55}^2}} = \sqrt {1,4175} \approx 1,19\)
b)
Phân tích chất lượng sản phẩm:
- Máy X: Như đã tính trước đó, giá trị trung bình là 30.27 mm và độ lệch chuẩn là 0.88 mm.
- Máy Y: Với giá trị trung bình mới là 30.55 mm và độ lệch chuẩn là 1.19 mm.
Kết luận:
- Máy X sản xuất sản phẩm có đường kính trung bình gần với giá trị mong muốn hơn (30,27 mm so với 30,4 mm), với độ lệch chuẩn nhỏ hơn, cho thấy sản phẩm đều hơn.
- Máy Y có giá trị trung bình lớn hơn 30,4 mm (30,55 mm), và độ lệch chuẩn cũng lớn hơn, cho thấy sản phẩm có sự biến thiên lớn hơn về kích thước, chất lượng không đồng đều bằng sản phẩm của máy X.
Do đó, sản phẩm của máy X vẫn được đánh giá là có chất lượng tốt hơn so với máy Y.
