Giải bài tập 2.27 trang 82 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 2.27 Trang 82 SGK Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.27 trang 82 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
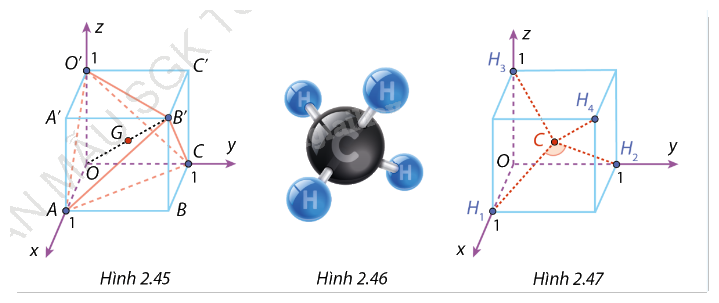
a) Trong không gian Oxyz, cho hình lập phương OABC.O’A’B’C’ với O(0;0;1), A(1;0;0), C(0;1;0) (Hình 2.45). G là trung điểm của đường chéo OB’ của hình lập phương. - Chứng minh rằng ACO’B’ là một tứ diện đều. - Tìm toạ độ các điểm B’ và G. Chứng minh rằng (overrightarrow {GA} + overrightarrow {GC} + overrightarrow {GO'} + overrightarrow {GB'} = vec 0). Điểm G được gọi là trọng tâm của tứ diện đều ACO’B’.
Đề bài
a) Trong không gian Oxyz, cho hình lập phương OABC.O’A’B’C’ với O(0;0;1), A(1;0;0), C(0;1;0) (Hình 2.45). G là trung điểm của đường chéo OB’ của hình lập phương.
- Chứng minh rằng ACO’B’ là một tứ diện đều.
- Tìm toạ độ các điểm B’ và G. Chứng minh rằng \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \vec 0\). Điểm G được gọi là trọng tâm của tứ diện đều ACO’B’.
b) Methane là một chất khí và là nguồn nguyên liệu quan trọng trong đời sống cũng như trong công nghiệp. Công thức phân tử của methane là \({\rm{C}}{{\rm{H}}_4}\). Mỗi phân tử \({\rm{C}}{{\rm{H}}_4}\) được cấu tạo bởi bốn nguyên tử hydrogen H và một nguyên tử carbon \(C\). Trong cấu tạo của phân tử methane, bốn nguyên tử hydrogen tạo thành bốn đỉnh của một tứ diện đều và nguyên tử carbon ở vị trí trọng tâm của tứ diện đó (Hình 2.46). Người ta gọi góc liên kết là góc tạo bởi liên kết \({\rm{H}} - {\rm{C}} - {\rm{H}}\). Đó là góc có hai cạnh là hai đoạn thẳng nối nguyên tử C với hai trong bốn nguyên tử H , chẳng hạn như \(\widehat {{{\rm{H}}_1}{\rm{C}}{{\rm{H}}_2}}\) (nguồn: https://www.worldatlas.com/space/why-methane-can-be-a-sign-of-life-outside-of-earth.html). Để tính góc liên kết trong phân tử methane, người ta chọn hệ trục toạ độ mà các nguyên tử hydrogen lẩn lượt nằm ở các vị trí \({H_1}(1;0;0),{H_2}(0;1;0)\), \({H_3}(0;0;1),{H_4}(1;1;1)\)(Hình 2.47). Tính số đo của góc liên kết (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
a)
- Sử dụng khái niệm của một tứ diện đều là các cạnh của nó bằng nhau.
- Tìm toạ độ của các điểm và vectơ cần thiết, sau đó áp dụng biểu thức toạ độ của tổng các vectơ để chứng minh.
b)
- Sử dụng biểu thức đã được chứng minh ở câu a để tìm toạ độ của C.
- Áp dụng công thức tính tích vô hướng của hai vectơ để tìm góc liên kết
\(\cos \theta = \frac{{\overrightarrow {C{H_1}} \cdot \overrightarrow {C{H_2}} }}{{\left| {\overrightarrow {C{H_1}} } \right|.\left| {\overrightarrow {C{H_2}} } \right|}}.\)
Lời giải chi tiết
a)
- Vì OABC.O’A’B’C’ là hình lập phương nên đường chéo của các mặt bên đều bằng nhau. Vậy ta có \(AC = AO' = AB' = CO' = CB' = O'B' = \sqrt 2 .\)
- Ta thấy tất cả các cạnh của tứ diện ACO’B’ đều có độ dài bằng \(\sqrt 2 \). Do đó, tứ diện ACO’B’ là tứ diện đều.
- Điểm B’ đối diện với điểm O qua hình lập phương, do đó tọa độ của B’ sẽ là: \(B'(1;1;1)\)
- Trung điểm G của đường chéo OB’: \(G = \left( {\frac{{0 + 1}}{2};\frac{{0 + 1}}{2};\frac{{1 + 0}}{2}} \right) = \left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\)
- Tính các vectơ:
\(\overrightarrow {GA} = A - G = \left( {1 - \frac{1}{2};0 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( {\frac{1}{2}; - \frac{1}{2}; - \frac{1}{2}} \right)\)\(\overrightarrow {GC} = C - G = \left( {0 - \frac{1}{2};1 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( { - \frac{1}{2};\frac{1}{2}; - \frac{1}{2}} \right)\)\(\overrightarrow {GO'} = O' - G = \left( {0 - \frac{1}{2};0 - \frac{1}{2};1 - \frac{1}{2}} \right) = \left( { - \frac{1}{2}; - \frac{1}{2};\frac{1}{2}} \right)\)\(\overrightarrow {GB'} = B' - G = \left( {1 - \frac{1}{2};1 - \frac{1}{2};1 - \frac{1}{2}} \right) = \left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\)
- Cộng các vectơ:
\(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \left( {\frac{1}{2} - \frac{1}{2} - \frac{1}{2} + \frac{1}{2}; - \frac{1}{2} + \frac{1}{2} - \frac{1}{2} + \frac{1}{2}; - \frac{1}{2} - \frac{1}{2} + \frac{1}{2} + \frac{1}{2}} \right) = \vec 0\)
- Vậy \(\overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GO'} + \overrightarrow {GB'} = \vec 0\).
b)
- Đặt toạ độ của C là \((x;y;z)\)
- Vì C là trọng tâm của tứ diện đều \({H_1}{H_2}{H_3}{H_4}\), áp dụng biểu thức đã chứng minh ở câu a, ta có: \(\overrightarrow {C{H_1}} + \overrightarrow {C{H_2}} + \overrightarrow {C{H_3}} + \overrightarrow {C{H_4}} = \overrightarrow 0 \)
- Thay các giá trị vào, ta được:
\((1 - x) + (0 - x) + (0 - x) + (1 - x) = 0 \Rightarrow x = \frac{1}{2}\)
\((0 - y) + (1 - y) + (0 - y) + (1 - y) = 0 \Rightarrow y = \frac{1}{2}\)
\((0 - z) + (0 - z) + (1 - z) + (1 - z) = 0 \Rightarrow z = \frac{1}{2}\)
- Vậy toạ độ của C là \(\left( {\frac{1}{2};\frac{1}{2};\frac{1}{2}} \right)\)
- Toạ độ của vectơ \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \) là:
\(\overrightarrow {C{H_1}} = \left( {1 - \frac{1}{2};0 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( {\frac{1}{2}; - \frac{1}{2}; - \frac{1}{2}} \right)\)
\(\overrightarrow {C{H_2}} = \left( {0 - \frac{1}{2};1 - \frac{1}{2};0 - \frac{1}{2}} \right) = \left( { - \frac{1}{2};\frac{1}{2}; - \frac{1}{2}} \right)\)
- Tích vô hướng của \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \):
\(\overrightarrow {C{H_1}} \cdot \overrightarrow {C{H_2}} = \left( {\frac{1}{2} \times - \frac{1}{2}} \right) + \left( { - \frac{1}{2} \times \frac{1}{2}} \right) + \left( { - \frac{1}{2} \times - \frac{1}{2}} \right) = - \frac{1}{4}\)
- Độ dài của \(\overrightarrow {C{H_1}} \)và \(\overrightarrow {C{H_2}} \) là: \(\left| {\overrightarrow {C{H_1}} } \right| = \left| {\overrightarrow {C{H_2}} } \right| = \frac{{\sqrt 3 }}{2}\)
- Số đo của góc liên kết là:
\(\cos \theta = \frac{{ - \frac{1}{4}}}{{\frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 3 }}{2}}} = - \frac{1}{3}\)
\(\theta = \arccos \left( { - \frac{1}{3}} \right) \approx {109.47^\circ }\)
Vậy góc liên kết \({{\rm{H}}_1} - {\rm{C}} - {{\rm{H}}_2}\) xấp xỉ \({109^\circ }\).
Giải Bài Tập 2.27 Trang 82 SGK Toán 12 Tập 1: Đạo Hàm và Khảo Sát Hàm Số
Bài tập 2.27 trang 82 SGK Toán 12 tập 1 yêu cầu chúng ta vận dụng kiến thức về đạo hàm để khảo sát hàm số, cụ thể là tìm khoảng đồng biến, nghịch biến và cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm cấp nhất (f'(x)): Sử dụng các quy tắc tính đạo hàm đã học.
- Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định.
- Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định bởi các điểm tới hạn để xác định khoảng đồng biến, nghịch biến.
- Xác định cực trị: Sử dụng dấu của f'(x) để xác định điểm cực đại, cực tiểu.
Lời Giải Chi Tiết Bài Tập 2.27
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử hàm số cần khảo sát là:
f(x) = x3 - 3x2 + 2
Bước 1: Tập xác định
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
Bước 2: Tính đạo hàm cấp nhất
f'(x) = 3x2 - 6x
Bước 3: Tìm các điểm tới hạn
Giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm tới hạn.
Bước 4: Lập bảng biến thiên
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Xác định cực trị
- Tại x = 0, f'(x) đổi dấu từ dương sang âm, do đó hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
- Tại x = 2, f'(x) đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.
Kết luận
Hàm số f(x) = x3 - 3x2 + 2 đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Lưu Ý Quan Trọng
Khi giải các bài tập về khảo sát hàm số, điều quan trọng là phải hiểu rõ các khái niệm về đạo hàm, điểm tới hạn, khoảng đồng biến, nghịch biến và cực trị. Việc lập bảng biến thiên một cách chính xác sẽ giúp bạn dễ dàng xác định được các đặc điểm của hàm số.
Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 2.27 trang 82 SGK Toán 12 tập 1. Chúc các em học tập tốt!