Giải mục 1 trang 74, 75, 76 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 74, 75, 76 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 74, 75, 76 SGK Toán 12 tập 1 tại tusach.vn.
Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của tusach.vn đã biên soạn bộ giải bài tập này với mục đích giúp các em hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
Trong không gian Oxyz, cho hai vectơ (vec a = ({x_1};{y_1};{z_1})) và (vec b = ({x_2};{y_2};{z_2})). a) Hãy biểu diễn các vectơ (vec a), (vec b) theo ba vectơ đơn vị (vec i), (vec j), (vec k). b) Tính (vec a + vec b) theo (vec i), (vec j), (vec k), từ đó tìm tọa độ của vectơ (vec a + vec b).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hai vectơ \(\vec a = ({x_1};{y_1};{z_1})\) và \(\vec b = ({x_2};{y_2};{z_2})\).
a) Hãy biểu diễn các vectơ \(\vec a\), \(\vec b\) theo ba vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\).
b) Tính \(\vec a + \vec b\) theo \(\vec i\), \(\vec j\), \(\vec k\), từ đó tìm tọa độ của vectơ \(\vec a + \vec b\).
Phương pháp giải:
- Mỗi vectơ trong không gian Oxyz với tọa độ (x,y,z) có thể được biểu diễn dưới dạng: \(\vec v = x\vec i + y\vec j + z\vec k\)
- Cộng các thành phần tương ứng của hai vectơ để tìm tổng: \(\vec a + \vec b = ({x_1} + {x_2})\vec i + ({y_1} + {y_2})\vec j + ({z_1} + {z_2})\vec k\)
Lời giải chi tiết:
a) Vectơ \(\vec a\) có tọa độ \(({x_1},{y_1},{z_1})\) nên nó có thể được biểu diễn theo các vectơ đơn vị \(\vec i,\vec j,\vec k\) như sau:
\(\vec a = {x_1}\vec i + {y_1}\vec j + {z_1}\vec k\)
Tương tự, vectơ \(\vec b\) có tọa độ \(({x_2},{y_2},{z_2})\) nên:
\(\vec b = {x_2}\vec i + {y_2}\vec j + {z_2}\vec k\)
b) Tổng của hai vectơ \(\vec a + \vec b\) là:
\(\vec a + \vec b = ({x_1}\vec i + {y_1}\vec j + {z_1}\vec k) + ({x_2}\vec i + {y_2}\vec j + {z_2}\vec k)\)
Kết hợp các thành phần tương ứng:
\(\vec a + \vec b = ({x_1} + {x_2})\vec i + ({y_1} + {y_2})\vec j + ({z_1} + {z_2})\vec k\)
Vậy tọa độ của vectơ \(\vec a + \vec b\) là \(({x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2})\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(5; -3; 0), B(2; 1; -1), C(4; 1; 2).
a) Tìm tọa độ của vectơ \(\vec u = 2\overrightarrow {AB} + \overrightarrow {AC} - 5\overrightarrow {BC} \).
b) Tìm điểm N sao cho \(2\overrightarrow {NA} = - \overrightarrow {NB} \)
Phương pháp giải:
a) Tính toạ độ của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) và \(\overrightarrow {BC} \) sau đó thay vào biểu thức để xác định toạ độ của \(\overrightarrow u \).
b)
- Gọi toạ độ của N là (x,y,z).
- Biểu diễn \(\overrightarrow {NA} ,\overrightarrow {NB} \) theo x, y, z.
- Sử dụng điều kiện \(2\overrightarrow {NA} = - \overrightarrow {NB} \) để thiết lập hệ phương trình.
- Giải hệ phương trình để tìm toạ độ N.
Lời giải chi tiết:
a) Trước hết, chúng ta tính các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {AC} \), và \(\overrightarrow {BC} \):
\(\overrightarrow {AB} = \vec B - \vec A = (2 - 5;1 + 3; - 1 - 0) = ( - 3;4; - 1)\)
\(\overrightarrow {AC} = \vec C - \vec A = (4 - 5;1 + 3;2 - 0) = ( - 1;4;2)\)
\(\overrightarrow {BC} = \vec C - \vec B = (4 - 2;1 - 1;2 + 1) = (2;0;3)\)
Bây giờ tính vectơ \(\vec u\):
\(\vec u = 2\overrightarrow {AB} + \overrightarrow {AC} - 5\overrightarrow {BC} \)
Thay các vectơ đã tính:
\(\vec u = 2( - 3;4; - 1) + ( - 1;4;2) - 5(2;0;3)\)
\(\vec u = ( - 6;8; - 2) + ( - 1;4;2) - (10;0;15)\)
\(\vec u = ( - 6 - 1 - 10;8 + 4 - 0; - 2 + 2 - 15)\)
\(\vec u = ( - 17;12; - 15)\)
Vậy tọa độ của vectơ \(\vec u\) là \(( - 17;12; - 15)\).
b) Điều kiện \(2\overrightarrow {NA} = - \overrightarrow {NB} \) có thể được viết lại như sau:
\(2\left( {\overrightarrow A - \overrightarrow N } \right) = \left( {\overrightarrow B - \overrightarrow N } \right)\)
Giải phương trình này:
\(2\overrightarrow A - 2\overrightarrow N = - \overrightarrow B + \overrightarrow N \)
Chuyển vế: \(3\vec N = 2\vec A + \vec B\)
Từ đó: \(\vec N = \frac{{2\vec A + \vec B}}{3}\)
Tính tọa độ của điểm N: \(\vec N = \frac{{2(5; - 3;0) + (2;1; - 1)}}{3}\)
\(\vec N = \frac{{(10; - 6;0) + (2;1; - 1)}}{3} = \frac{{(12; - 5; - 1)}}{3}\)
\(\vec N = \left( {4; - \frac{5}{3}; - \frac{1}{3}} \right)\)
Vậy tọa độ của điểm N là \(\left( {4; - \frac{5}{3}; - \frac{1}{3}} \right)\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(4; 1; -1), B(2; -1; 5), C(3; 0; 2). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Phương pháp giải:
Ba điểm A, B, C thẳng hàng khi và chỉ khi vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
Lời giải chi tiết:
Tính các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = \vec B - \vec A = (2 - 4; - 1 - 1;5 + 1) = ( - 2; - 2;6)\)
\(\overrightarrow {AC} = \vec C - \vec A = (3 - 4;0 - 1;2 + 1) = ( - 1; - 1;3)\)
Xét tỉ lệ:
\(\frac{{ - 2}}{{ - 1}} = 2,\quad \frac{{ - 2}}{{ - 1}} = 2,\quad \frac{6}{3} = 2\)
Vì \(\frac{{\overrightarrow {AB} }}{{\overrightarrow {AC} }} = 2\), hai vectơ này cùng phương, nên ba điểm A, B, C thẳng hàng.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tam giác ABC có \(A\left( {{x_A},{y_A},{z_A}} \right)\), \(B\left( {{x_B},{y_B},{z_B}} \right)\), và \(C\left( {{x_C},{y_C},{z_C}} \right)\)
a) Gọi M là trung điểm của đoạn thẳng A B. Tìm tọa độ điểm M.
b) Gọi G là trọng tâm tam giác ABC. Tìm tọa độ điểm G.
Phương pháp giải:
- Công thức trung điểm: Tọa độ trung điểm M của đoạn thẳng nối hai điểm \(A\left( {{x_A},{y_A},{z_A}} \right)\) và \(B\left( {{x_B},{y_B},{z_B}} \right)\) được tính theo công thức:
\(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
- Công thức trọng tâm: Tọa độ trọng tâm G của tam giác có các đỉnh \(A\left( {{x_A},{y_A},{z_A}} \right),B\left( {{x_B},{y_B},{z_B}} \right)\), và \(C\left( {{x_C},{y_C},{z_C}} \right)\) được tính theo công thức:
\(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Lời giải chi tiết:
a) Tọa độ điểm M là: \(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
b) Tọa độ điểm G là: \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(A(1;3; - 5)\), \(M\left( {\frac{3}{2};2; - \frac{1}{2}} \right)\), \(G\left( {2;\frac{2}{3}; - \frac{2}{3}} \right)\).
a) Tìm tọa độ điểm B sao cho M là trung điểm của đoạn thẳng AB.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Phương pháp giải:
- Tọa độ điểm B: Sử dụng công thức trung điểm:
\({x_B} = 2{x_M} - {x_A},\quad {y_B} = 2{y_M} - {y_A},\quad {z_B} = 2{z_M} - {z_A}\).
Thay tọa độ A và M để tìm B.
- Tọa độ điểm C: Sử dụng công thức trọng tâm:
\({x_C} = 3{x_G} - ({x_A} + {x_B}),\quad {y_C} = 3{y_G} - ({y_A} + {y_B}),\quad {z_C} = 3{z_G} - ({z_A} + {z_B})\).
Thay tọa độ A, B, và G để tìm C.
Lời giải chi tiết:
a) Ta có tọa độ điểm M là trung điểm của AB nên:
\(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
Từ đó, tọa độ điểm B được xác định bằng cách giải phương trình:
\({x_B} = 2{x_M} - {x_A},\quad {y_B} = 2{y_M} - {y_A},\quad {z_B} = 2{z_M} - {z_A}\)
Thay toạ độ của điểm A, M vào:
\({x_B} = 2 \times \frac{3}{2} - 1 = 2,\quad {y_B} = 2 \times 2 - 3 = 1,\quad {z_B} = 2 \times \left( { - \frac{1}{2}} \right) - ( - 5) = 4\)
Vậy tọa độ điểm B là B(2; 1; 4).
b)
Vì G là trọng tâm của tam giác ABC, ta có:
\(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Từ đó, ta có hệ phương trình:
\({x_C} = 3{x_G} - ({x_A} + {x_B}),\quad {y_C} = 3{y_G} - ({y_A} + {y_B}),\quad {z_C} = 3{z_G} - ({z_A} + {z_B})\)
Thay toạ độ của điểm A, B, G vào:
\({x_C} = 3 \times 2 - (1 + 2) = 3, \quad {y_C} = 3 \times \frac{2}{3} - (3 + 1) = 0,\quad {z_C} = 3 \times \left( { - \frac{2}{3}} \right) - ( - 5 + 4) = - 3\)
Vậy tọa độ điểm C là C (3; 0; -3).
VD1
Trả lời câu hỏi Vận dụng 1 trang 75 SGK Toán 12 Cùng khám phá
Trong Hình 2.41, gốc tọa độ O là nơi máy bay xuất phát, trục Ox theo hướng Nam, trục Oy theo hướng Đông, trục Oz theo hướng thẳng đứng. Đơn vị trên các trục là km. Vào thời điểm 9h30 sáng, máy bay ở độ cao 9 km, cách điểm xuất phát theo hướng Nam 150 km và theo hướng Đông 300 km. Phi công để chế độ bay tự động, với vận tốc theo hướng Đông 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng Bắc với vận tốc 10 m/s. Tìm tọa độ của máy bay lúc 10h30, với giả định là trong khoảng thời gian 9h30 đến 10h30, vận tốc và hướng của gió không thay đổi.
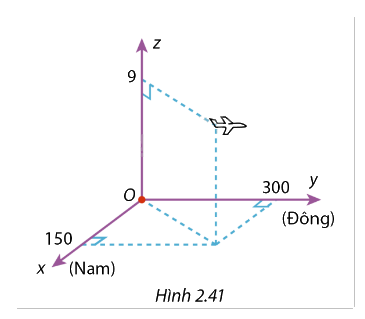
Phương pháp giải:
- Tìm tọa độ của máy bay tại thời điểm ban đầu.
- Tính vận tốc của máy bay theo các trục Ox, Oy (bao gồm cả ảnh hưởng của gió) và xác định vận tốc theo trục Oz.
- Sử dụng công thức \(x = {x_0} + {v_x} \times t\), \(y = {y_0} + {v_y} \times t\), \(z = {z_0} + {v_z} \times t\) để tính tọa độ máy bay sau thời gian \(t\).
Lời giải chi tiết:
Tọa độ máy bay lúc 9h30 là: A = (150; 300; 9).
Vận tốc gió là 10 m/s = 36 km/h.
Hướng di chuyển của máy bay trong 1 giờ là: \(\overrightarrow v = ( - 36;750;0)\).
Tọa độ của máy bay lúc 10h30 là: B = (150 – 36; 300 + 750; 9 + 0) = (114; 1050; 9).
- HĐ1
- LT1
- LT2
- VD1
- HĐ2
- LT3
Trả lời câu hỏi Hoạt động 1 trang 74 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho hai vectơ \(\vec a = ({x_1};{y_1};{z_1})\) và \(\vec b = ({x_2};{y_2};{z_2})\).
a) Hãy biểu diễn các vectơ \(\vec a\), \(\vec b\) theo ba vectơ đơn vị \(\vec i\), \(\vec j\), \(\vec k\).
b) Tính \(\vec a + \vec b\) theo \(\vec i\), \(\vec j\), \(\vec k\), từ đó tìm tọa độ của vectơ \(\vec a + \vec b\).
Phương pháp giải:
- Mỗi vectơ trong không gian Oxyz với tọa độ (x,y,z) có thể được biểu diễn dưới dạng: \(\vec v = x\vec i + y\vec j + z\vec k\)
- Cộng các thành phần tương ứng của hai vectơ để tìm tổng: \(\vec a + \vec b = ({x_1} + {x_2})\vec i + ({y_1} + {y_2})\vec j + ({z_1} + {z_2})\vec k\)
Lời giải chi tiết:
a) Vectơ \(\vec a\) có tọa độ \(({x_1},{y_1},{z_1})\) nên nó có thể được biểu diễn theo các vectơ đơn vị \(\vec i,\vec j,\vec k\) như sau:
\(\vec a = {x_1}\vec i + {y_1}\vec j + {z_1}\vec k\)
Tương tự, vectơ \(\vec b\) có tọa độ \(({x_2},{y_2},{z_2})\) nên:
\(\vec b = {x_2}\vec i + {y_2}\vec j + {z_2}\vec k\)
b) Tổng của hai vectơ \(\vec a + \vec b\) là:
\(\vec a + \vec b = ({x_1}\vec i + {y_1}\vec j + {z_1}\vec k) + ({x_2}\vec i + {y_2}\vec j + {z_2}\vec k)\)
Kết hợp các thành phần tương ứng:
\(\vec a + \vec b = ({x_1} + {x_2})\vec i + ({y_1} + {y_2})\vec j + ({z_1} + {z_2})\vec k\)
Vậy tọa độ của vectơ \(\vec a + \vec b\) là \(({x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2})\).
Trả lời câu hỏi Luyện tập 1 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(5; -3; 0), B(2; 1; -1), C(4; 1; 2).
a) Tìm tọa độ của vectơ \(\vec u = 2\overrightarrow {AB} + \overrightarrow {AC} - 5\overrightarrow {BC} \).
b) Tìm điểm N sao cho \(2\overrightarrow {NA} = - \overrightarrow {NB} \)
Phương pháp giải:
a) Tính toạ độ của các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} \) và \(\overrightarrow {BC} \) sau đó thay vào biểu thức để xác định toạ độ của \(\overrightarrow u \).
b)
- Gọi toạ độ của N là (x,y,z).
- Biểu diễn \(\overrightarrow {NA} ,\overrightarrow {NB} \) theo x, y, z.
- Sử dụng điều kiện \(2\overrightarrow {NA} = - \overrightarrow {NB} \) để thiết lập hệ phương trình.
- Giải hệ phương trình để tìm toạ độ N.
Lời giải chi tiết:
a) Trước hết, chúng ta tính các vectơ \(\overrightarrow {AB} \), \(\overrightarrow {AC} \), và \(\overrightarrow {BC} \):
\(\overrightarrow {AB} = \vec B - \vec A = (2 - 5;1 + 3; - 1 - 0) = ( - 3;4; - 1)\)
\(\overrightarrow {AC} = \vec C - \vec A = (4 - 5;1 + 3;2 - 0) = ( - 1;4;2)\)
\(\overrightarrow {BC} = \vec C - \vec B = (4 - 2;1 - 1;2 + 1) = (2;0;3)\)
Bây giờ tính vectơ \(\vec u\):
\(\vec u = 2\overrightarrow {AB} + \overrightarrow {AC} - 5\overrightarrow {BC} \)
Thay các vectơ đã tính:
\(\vec u = 2( - 3;4; - 1) + ( - 1;4;2) - 5(2;0;3)\)
\(\vec u = ( - 6;8; - 2) + ( - 1;4;2) - (10;0;15)\)
\(\vec u = ( - 6 - 1 - 10;8 + 4 - 0; - 2 + 2 - 15)\)
\(\vec u = ( - 17;12; - 15)\)
Vậy tọa độ của vectơ \(\vec u\) là \(( - 17;12; - 15)\).
b) Điều kiện \(2\overrightarrow {NA} = - \overrightarrow {NB} \) có thể được viết lại như sau:
\(2\left( {\overrightarrow A - \overrightarrow N } \right) = \left( {\overrightarrow B - \overrightarrow N } \right)\)
Giải phương trình này:
\(2\overrightarrow A - 2\overrightarrow N = - \overrightarrow B + \overrightarrow N \)
Chuyển vế: \(3\vec N = 2\vec A + \vec B\)
Từ đó: \(\vec N = \frac{{2\vec A + \vec B}}{3}\)
Tính tọa độ của điểm N: \(\vec N = \frac{{2(5; - 3;0) + (2;1; - 1)}}{3}\)
\(\vec N = \frac{{(10; - 6;0) + (2;1; - 1)}}{3} = \frac{{(12; - 5; - 1)}}{3}\)
\(\vec N = \left( {4; - \frac{5}{3}; - \frac{1}{3}} \right)\)
Vậy tọa độ của điểm N là \(\left( {4; - \frac{5}{3}; - \frac{1}{3}} \right)\).
Trả lời câu hỏi Luyện tập 2 trang 75 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm A(4; 1; -1), B(2; -1; 5), C(3; 0; 2). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Phương pháp giải:
Ba điểm A, B, C thẳng hàng khi và chỉ khi vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
Lời giải chi tiết:
Tính các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = \vec B - \vec A = (2 - 4; - 1 - 1;5 + 1) = ( - 2; - 2;6)\)
\(\overrightarrow {AC} = \vec C - \vec A = (3 - 4;0 - 1;2 + 1) = ( - 1; - 1;3)\)
Xét tỉ lệ:
\(\frac{{ - 2}}{{ - 1}} = 2,\quad \frac{{ - 2}}{{ - 1}} = 2,\quad \frac{6}{3} = 2\)
Vì \(\frac{{\overrightarrow {AB} }}{{\overrightarrow {AC} }} = 2\), hai vectơ này cùng phương, nên ba điểm A, B, C thẳng hàng.
Trả lời câu hỏi Vận dụng 1 trang 75 SGK Toán 12 Cùng khám phá
Trong Hình 2.41, gốc tọa độ O là nơi máy bay xuất phát, trục Ox theo hướng Nam, trục Oy theo hướng Đông, trục Oz theo hướng thẳng đứng. Đơn vị trên các trục là km. Vào thời điểm 9h30 sáng, máy bay ở độ cao 9 km, cách điểm xuất phát theo hướng Nam 150 km và theo hướng Đông 300 km. Phi công để chế độ bay tự động, với vận tốc theo hướng Đông 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng Bắc với vận tốc 10 m/s. Tìm tọa độ của máy bay lúc 10h30, với giả định là trong khoảng thời gian 9h30 đến 10h30, vận tốc và hướng của gió không thay đổi.
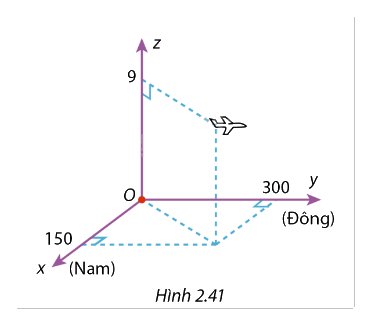
Phương pháp giải:
- Tìm tọa độ của máy bay tại thời điểm ban đầu.
- Tính vận tốc của máy bay theo các trục Ox, Oy (bao gồm cả ảnh hưởng của gió) và xác định vận tốc theo trục Oz.
- Sử dụng công thức \(x = {x_0} + {v_x} \times t\), \(y = {y_0} + {v_y} \times t\), \(z = {z_0} + {v_z} \times t\) để tính tọa độ máy bay sau thời gian \(t\).
Lời giải chi tiết:
Tọa độ máy bay lúc 9h30 là: A = (150; 300; 9).
Vận tốc gió là 10 m/s = 36 km/h.
Hướng di chuyển của máy bay trong 1 giờ là: \(\overrightarrow v = ( - 36;750;0)\).
Tọa độ của máy bay lúc 10h30 là: B = (150 – 36; 300 + 750; 9 + 0) = (114; 1050; 9).
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tam giác ABC có \(A\left( {{x_A},{y_A},{z_A}} \right)\), \(B\left( {{x_B},{y_B},{z_B}} \right)\), và \(C\left( {{x_C},{y_C},{z_C}} \right)\)
a) Gọi M là trung điểm của đoạn thẳng A B. Tìm tọa độ điểm M.
b) Gọi G là trọng tâm tam giác ABC. Tìm tọa độ điểm G.
Phương pháp giải:
- Công thức trung điểm: Tọa độ trung điểm M của đoạn thẳng nối hai điểm \(A\left( {{x_A},{y_A},{z_A}} \right)\) và \(B\left( {{x_B},{y_B},{z_B}} \right)\) được tính theo công thức:
\(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
- Công thức trọng tâm: Tọa độ trọng tâm G của tam giác có các đỉnh \(A\left( {{x_A},{y_A},{z_A}} \right),B\left( {{x_B},{y_B},{z_B}} \right)\), và \(C\left( {{x_C},{y_C},{z_C}} \right)\) được tính theo công thức:
\(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Lời giải chi tiết:
a) Tọa độ điểm M là: \(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
b) Tọa độ điểm G là: \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Trả lời câu hỏi Luyện tập 3 trang 76 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(A(1;3; - 5)\), \(M\left( {\frac{3}{2};2; - \frac{1}{2}} \right)\), \(G\left( {2;\frac{2}{3}; - \frac{2}{3}} \right)\).
a) Tìm tọa độ điểm B sao cho M là trung điểm của đoạn thẳng AB.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Phương pháp giải:
- Tọa độ điểm B: Sử dụng công thức trung điểm:
\({x_B} = 2{x_M} - {x_A},\quad {y_B} = 2{y_M} - {y_A},\quad {z_B} = 2{z_M} - {z_A}\).
Thay tọa độ A và M để tìm B.
- Tọa độ điểm C: Sử dụng công thức trọng tâm:
\({x_C} = 3{x_G} - ({x_A} + {x_B}),\quad {y_C} = 3{y_G} - ({y_A} + {y_B}),\quad {z_C} = 3{z_G} - ({z_A} + {z_B})\).
Thay tọa độ A, B, và G để tìm C.
Lời giải chi tiết:
a) Ta có tọa độ điểm M là trung điểm của AB nên:
\(M\left( {\frac{{{x_A} + {x_B}}}{2},\frac{{{y_A} + {y_B}}}{2},\frac{{{z_A} + {z_B}}}{2}} \right)\)
Từ đó, tọa độ điểm B được xác định bằng cách giải phương trình:
\({x_B} = 2{x_M} - {x_A},\quad {y_B} = 2{y_M} - {y_A},\quad {z_B} = 2{z_M} - {z_A}\)
Thay toạ độ của điểm A, M vào:
\({x_B} = 2 \times \frac{3}{2} - 1 = 2,\quad {y_B} = 2 \times 2 - 3 = 1,\quad {z_B} = 2 \times \left( { - \frac{1}{2}} \right) - ( - 5) = 4\)
Vậy tọa độ điểm B là B(2; 1; 4).
b)
Vì G là trọng tâm của tam giác ABC, ta có:
\(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3},\frac{{{y_A} + {y_B} + {y_C}}}{3},\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
Từ đó, ta có hệ phương trình:
\({x_C} = 3{x_G} - ({x_A} + {x_B}),\quad {y_C} = 3{y_G} - ({y_A} + {y_B}),\quad {z_C} = 3{z_G} - ({z_A} + {z_B})\)
Thay toạ độ của điểm A, B, G vào:
\({x_C} = 3 \times 2 - (1 + 2) = 3, \quad {y_C} = 3 \times \frac{2}{3} - (3 + 1) = 0,\quad {z_C} = 3 \times \left( { - \frac{2}{3}} \right) - ( - 5 + 4) = - 3\)
Vậy tọa độ điểm C là C (3; 0; -3).
Giải mục 1 trang 74, 75, 76 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 1 của SGK Toán 12 tập 1 thường xoay quanh các kiến thức cơ bản về đạo hàm, bao gồm định nghĩa, ý nghĩa hình học và các quy tắc tính đạo hàm của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của Mục 1 SGK Toán 12 tập 1
- Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và trên một khoảng.
- Ý nghĩa hình học của đạo hàm: Mối liên hệ giữa đạo hàm và hệ số góc của tiếp tuyến của đồ thị hàm số.
- Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Đạo hàm của một số hàm số cơ bản: Biết cách tính đạo hàm của các hàm số thường gặp như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
Hướng dẫn giải bài tập trang 74, 75, 76 SGK Toán 12 tập 1
Để giải tốt các bài tập trong mục này, các em cần:
- Nắm vững lý thuyết: Đọc kỹ SGK, ghi chép đầy đủ các định nghĩa, quy tắc và ví dụ.
- Luyện tập thường xuyên: Làm nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Phân tích bài toán: Đọc kỹ đề bài, xác định đúng yêu cầu và lựa chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Giải chi tiết một số bài tập tiêu biểu
Bài 1 (trang 74): Tính đạo hàm của hàm số f(x) = x2 + 3x - 2.
Lời giải:
f'(x) = 2x + 3
Bài 2 (trang 75): Tìm hệ số góc của tiếp tuyến của đồ thị hàm số y = x3 - 2x + 1 tại điểm có hoành độ x = 1.
Lời giải:
y' = 3x2 - 2
Tại x = 1, y' = 3(1)2 - 2 = 1. Vậy hệ số góc của tiếp tuyến là 1.
Bài 3 (trang 76): Tính đạo hàm của hàm số y = sin(2x).
Lời giải:
y' = cos(2x) * 2 = 2cos(2x)
Lưu ý quan trọng
Trong quá trình giải bài tập, các em cần chú ý đến các quy tắc tính đạo hàm và các công thức liên quan. Ngoài ra, việc vẽ đồ thị hàm số cũng có thể giúp các em hiểu rõ hơn về ý nghĩa hình học của đạo hàm.
Tusach.vn – Đồng hành cùng các em trên con đường học tập
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết để giúp các em học tốt môn Toán 12. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Bài tập | Lời giải |
|---|---|
| Bài 1 (trang 74) | f'(x) = 2x + 3 |
| Bài 2 (trang 75) | Hệ số góc = 1 |
| Bài 3 (trang 76) | y' = 2cos(2x) |