Giải bài tập 1.35 trang 46 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải bài tập 1.35 trang 46 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.35 trang 46 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
tusach.vn sẽ giúp các em hiểu rõ cách giải bài tập này một cách nhanh chóng và hiệu quả nhất.
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: a) \(y = \frac{{3x + 6}}{{2 - x}}\) b) \(y = 2x + \frac{3}{{2 - x}}\)
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau:
a) \(y = \frac{{3x + 6}}{{2 - x}}\)
b) \(y = 2x + \frac{3}{{2 - x}}\)
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị hàm số
Lời giải chi tiết
a)
- Tập xác định: \(D = R\backslash \{ 2\} \)
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x + 6}}{{2 - x}} = - 3\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x + 6}}{{2 - x}} = - 3\)
Suy ra đường thẳng \({\rm{y}} = - 3\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{3x + 6}}{{2 - x}} = - \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x + 6}}{{2 - x}} = \infty \)
Suy ra đường thẳng \({\rm{x}} = 2\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{12}}{{{{(2 - x)}^2}}} > 0\forall x \in D\)
Suy ra hàm số đồng biến trên tập xác định
Bảng biến thiên:
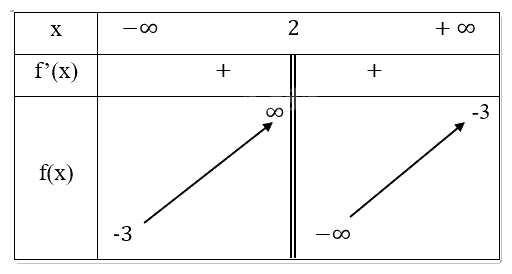
Cực trị: Hàm số không có cực trị
- Vẽ đồ thị
Tiệm cận đứng: \(x = 2\) và tiệm cận ngang \(y = - 3\)
Giao với trục Oy tại điểm (0,3)
Giao với trục Ox tại điểm (-2,0)
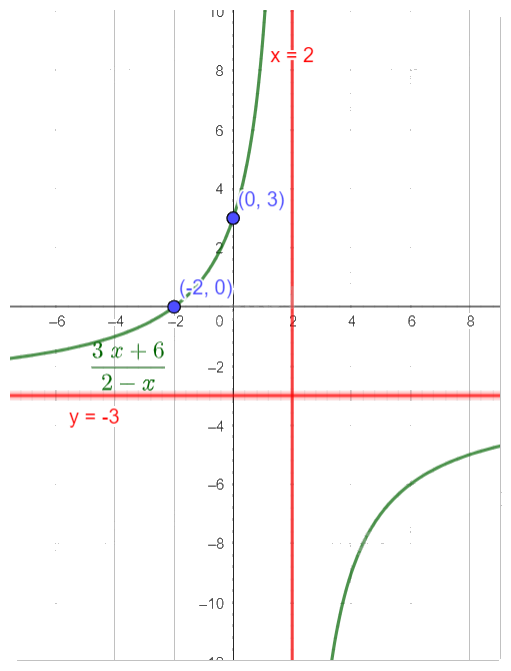
b)
- Tập xác định: \(D = R\backslash \{ 2\} \)
- Sự biến thiên:
Giới hạn, tiệm cận:
\[\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + \frac{3}{{2 - x}}} \right) = \infty \]
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + \frac{3}{{2 - x}}} \right) = - \infty \)
Suy ra hàm số không có tiệm cận ngang
\(\mathop {\lim }\limits_{x \to {2^ + }} f(x) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {2x + \frac{3}{{2 - x}}} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + \frac{3}{{2 - x}}} \right) = \infty \)
Suy ra đường thẳng \({\rm{x}} = 2\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Khi \(x \to \pm \infty ,\frac{3}{{2 - x}} \to 0\)nên đường thẳng \(y = 2x\) là tiệm cận xiên của đồ thị hàm số đã cho.
Ta có: \({y^\prime } = 2 + \frac{3}{{{{(2 - x)}^2}}} > 0\forall x \in D\)
Suy ra hàm số đồng biến trên tập xác định
Bảng biến thiên:
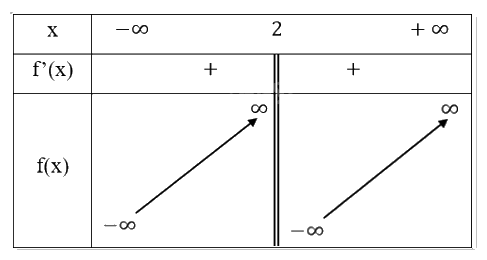
- Vẽ đồ thị
Giao điểm với trục Ox là \(\left( {\frac{{2 + \sqrt {10} }}{2};0} \right),\left( {\frac{{2 - \sqrt {10} }}{2};0} \right)\)
Giao điểm với trục Oy là \(\left( {0;\frac{3}{2}} \right)\)
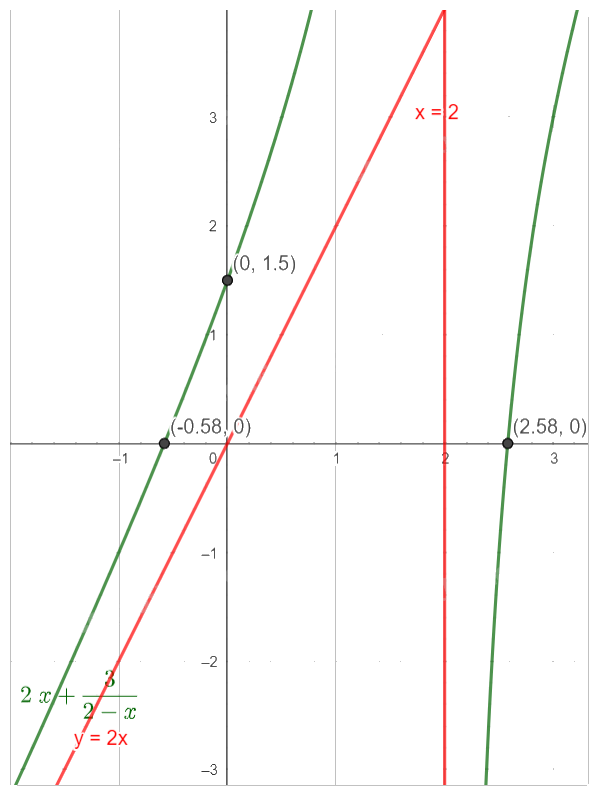
Giải bài tập 1.35 trang 46 SGK Toán 12 tập 1: Đề bài
Bài tập 1.35 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Cụ thể, đề bài thường cho một hàm số bậc ba hoặc bậc bốn và yêu cầu:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất và đạo hàm bậc hai của hàm số.
- Tìm các điểm cực trị của hàm số (điểm cực đại, điểm cực tiểu).
- Khảo sát sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Phương pháp giải bài tập 1.35 trang 46 SGK Toán 12 tập 1
Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
- Kiến thức về đạo hàm: Hiểu rõ định nghĩa, tính chất và các quy tắc tính đạo hàm.
- Điều kiện cực trị: Nắm vững điều kiện cần và đủ để một điểm là điểm cực trị của hàm số.
- Khảo sát hàm số: Biết cách sử dụng đạo hàm để khảo sát sự biến thiên của hàm số (khoảng đồng biến, nghịch biến, cực trị, giới hạn).
Lời giải chi tiết bài tập 1.35 trang 46 SGK Toán 12 tập 1 (Ví dụ)
Giả sử đề bài cho hàm số: y = x3 - 3x2 + 2
Bước 1: Xác định tập xác định
Hàm số y = x3 - 3x2 + 2 là hàm đa thức nên tập xác định của hàm số là D = ℝ.
Bước 2: Tính đạo hàm bậc nhất và bậc hai
y' = 3x2 - 6x
y'' = 6x - 6
Bước 3: Tìm các điểm cực trị
Giải phương trình y' = 0: 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Xét dấu y' trên các khoảng xác định:
- Khi x < 0: y' > 0 (hàm số đồng biến)
- Khi 0 < x < 2: y' < 0 (hàm số nghịch biến)
- Khi x > 2: y' > 0 (hàm số đồng biến)
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại là y(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là y(2) = -2.
Bước 4: Khảo sát sự biến thiên và vẽ đồ thị
Dựa vào bảng biến thiên và các điểm cực trị, ta có thể vẽ được đồ thị hàm số.
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các bước tính toán đạo hàm.
- Sử dụng bảng biến thiên để xác định khoảng đồng biến, nghịch biến và cực trị một cách chính xác.
- Vẽ đồ thị hàm số để kiểm tra lại kết quả.
Tổng kết
Bài tập 1.35 trang 46 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với lời giải chi tiết và phương pháp giải trên, các em sẽ tự tin hơn khi giải các bài tập tương tự.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi tại tusach.vn. Chúng tôi luôn sẵn sàng hỗ trợ các em!