Giải mục 1 trang 2,3,4 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 2,3,4 SGK Toán 12 tập 1 - Cùng khám phá
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 2,3,4 SGK Toán 12 tập 1. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em hiểu rõ kiến thức và tự tin làm bài tập.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích từng bài tập một cách dễ hiểu, đảm bảo các em có thể tự học và nâng cao kết quả học tập.
Tính đơn điệu của hàm số và dấu của đạo hàm
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 4 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)
Phương pháp giải:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\) và\({x_1} > {x_2}\)
Xét dấu của \(f({x_1}) - f({x_2})\)
b) Tính \(f'(x)\) qua đó xét dấu của \(f'(x)\)
Lời giải chi tiết:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\)và \({x_1} > {x_2}\)
Ta có: \(f({x_1}) - f({x_2})\)= \(({x_1} + 1) - ({x_2} + 1)\)= \({x_1} - {x_2}\)
Mà \({x_1} > {x_2}\) \( \Rightarrow {x_1} - {x_2} > 0\)
Nên \(f({x_1}) - f({x_2}) > 0\) \( \Rightarrow f({x_1}) > f({x_2})\)
Suy ra hàm số \(y = f(x) = {x^3} + 1\) đồng biến trên \(R\)
b) Ta có: \(f'(x) = 3{x^2}\)
Vì \(3{x^2} > 0\) với \(\forall x \in R\)
Nên \(f'(x) > 0\) với \(\forall x \in R\)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 2 SGK Toán 12 Cùng khám phá
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
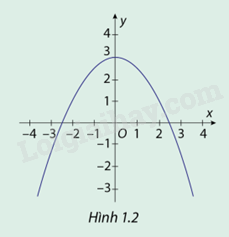
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
c) Ghi lại và hoàn thành bảng biến thiên sau
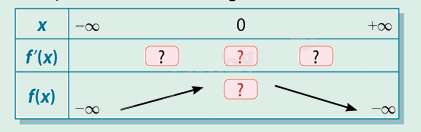
Phương pháp giải:
a) Sử dụng khái niệm hàm số đồng biến, hàm số nghịch biến trên khoảng (a;b)
Hàm số \(y = f(x)\)gọi là đồng biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} < {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
Hàm số \(y = f(x)\) gọi là nghịch biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} > {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
b) Chọn vài giá trị của x nằm trong khoảng đồng biến , nghịch biến ở câu a rồi thay vào \(f'(x)\)xem \(f'(x)\) có giá trị âm hay dương.
c) Áp dụng kết quả câu a và câu b rồi điền vào
Lời giải chi tiết:
a) Hàm số \(y = f(x)\) xác định trên R
Nhìn hình 1.2 ta thấy:
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) đồng biến trên khoảng \(( - \infty ;0)\)
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) nghịch biến trên khoảng \((0; + \infty )\)
b) Ta có \(f'(x) = - x\)
Ta thấy: Với \(x > 0\)thì \(f'(x) < 0\)
Với \(x < 0\) thì \(f'(x) > 0\)
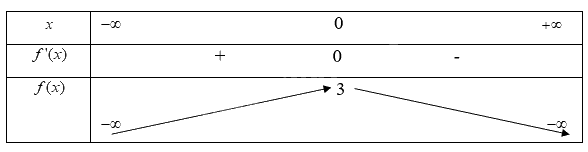
c)
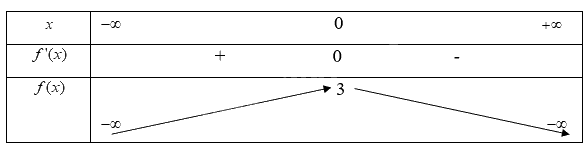
LT2
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 12 Kết nối tri thức
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)
Phương pháp giải:
Bước 1: tính đạo hàm \(y'\)
Bước 2: xét dấu \(y'\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số
Lời giải chi tiết:
Hàm số đã cho xác định trên
Ta có: \(y' = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y' \le 0\)với \(\forall x \in R\)và \(y' = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
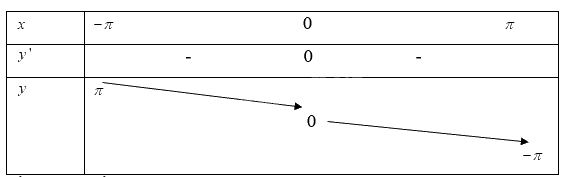
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
LT1
Trả lời câu hỏi Luyện tập 1 trang 4 SGK Toán 12 Kết nối tri thức
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Phương pháp giải:
Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên
Lời giải chi tiết:
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
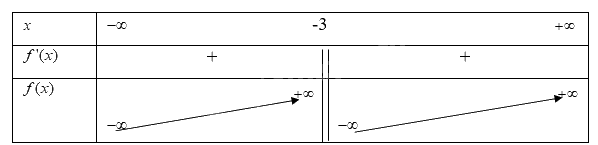
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
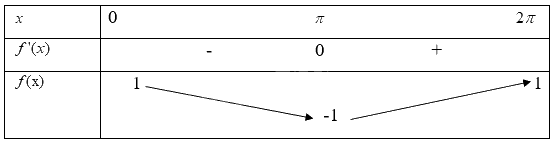
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
- HĐ1
- LT1
- HĐ2
- LT2
Trả lời câu hỏi Hoạt động 1 trang 2 SGK Toán 12 Cùng khám phá
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
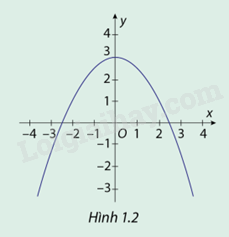
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
c) Ghi lại và hoàn thành bảng biến thiên sau
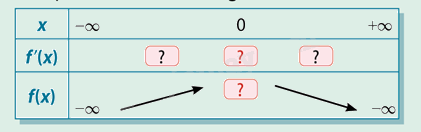
Phương pháp giải:
a) Sử dụng khái niệm hàm số đồng biến, hàm số nghịch biến trên khoảng (a;b)
Hàm số \(y = f(x)\)gọi là đồng biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} < {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
Hàm số \(y = f(x)\) gọi là nghịch biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} > {x_2}\) thì ta có \(f({x_1}) < f({x_2})\)
b) Chọn vài giá trị của x nằm trong khoảng đồng biến , nghịch biến ở câu a rồi thay vào \(f'(x)\)xem \(f'(x)\) có giá trị âm hay dương.
c) Áp dụng kết quả câu a và câu b rồi điền vào
Lời giải chi tiết:
a) Hàm số \(y = f(x)\) xác định trên R
Nhìn hình 1.2 ta thấy:
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) đồng biến trên khoảng \(( - \infty ;0)\)
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) nghịch biến trên khoảng \((0; + \infty )\)
b) Ta có \(f'(x) = - x\)
Ta thấy: Với \(x > 0\)thì \(f'(x) < 0\)
Với \(x < 0\) thì \(f'(x) > 0\)
c)
Trả lời câu hỏi Luyện tập 1 trang 4 SGK Toán 12 Kết nối tri thức
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Phương pháp giải:
Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên
Lời giải chi tiết:
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
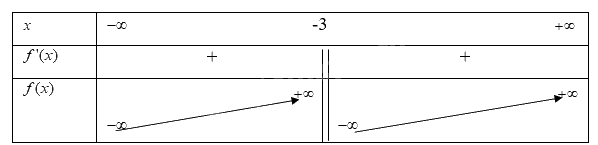
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
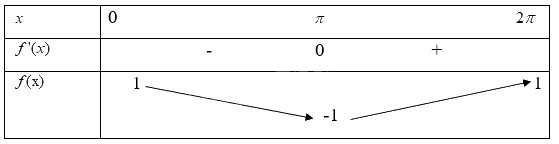
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
Trả lời câu hỏi Hoạt động 2 trang 4 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)
Phương pháp giải:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\) và\({x_1} > {x_2}\)
Xét dấu của \(f({x_1}) - f({x_2})\)
b) Tính \(f'(x)\) qua đó xét dấu của \(f'(x)\)
Lời giải chi tiết:
a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\)và \({x_1} > {x_2}\)
Ta có: \(f({x_1}) - f({x_2})\)= \(({x_1} + 1) - ({x_2} + 1)\)= \({x_1} - {x_2}\)
Mà \({x_1} > {x_2}\) \( \Rightarrow {x_1} - {x_2} > 0\)
Nên \(f({x_1}) - f({x_2}) > 0\) \( \Rightarrow f({x_1}) > f({x_2})\)
Suy ra hàm số \(y = f(x) = {x^3} + 1\) đồng biến trên \(R\)
b) Ta có: \(f'(x) = 3{x^2}\)
Vì \(3{x^2} > 0\) với \(\forall x \in R\)
Nên \(f'(x) > 0\) với \(\forall x \in R\)
Trả lời câu hỏi Luyện tập 2 trang 5 SGK Toán 12 Kết nối tri thức
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)
Phương pháp giải:
Bước 1: tính đạo hàm \(y'\)
Bước 2: xét dấu \(y'\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số
Lời giải chi tiết:
Hàm số đã cho xác định trên
Ta có: \(y' = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y' \le 0\)với \(\forall x \in R\)và \(y' = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
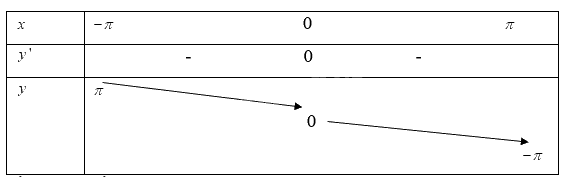
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
Giải mục 1 trang 2,3,4 SGK Toán 12 tập 1 - Cùng khám phá: Tổng quan và Hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 1 thường xoay quanh các kiến thức cơ bản về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Nội dung chính của Mục 1 SGK Toán 12 tập 1
- Định nghĩa hàm số bậc hai: Hàm số có dạng y = ax2 + bx + c, với a ≠ 0.
- Hệ số a và tính chất của đồ thị: Xác định chiều mở của parabol (lên trên nếu a > 0, xuống dưới nếu a < 0).
- Đỉnh của parabol: Công thức tính tọa độ đỉnh I(x0; y0) với x0 = -b/2a và y0 = -Δ/4a (Δ = b2 - 4ac).
- Trục đối xứng của parabol: Đường thẳng x = x0.
- Giao điểm của parabol với trục hoành (Ox): Nghiệm của phương trình ax2 + bx + c = 0.
- Giao điểm của parabol với trục tung (Oy): Điểm có tọa độ (0; c).
Giải chi tiết các bài tập trang 2,3,4 SGK Toán 12 tập 1
Bài 1: Xác định hệ số a, b, c của hàm số
Bài tập này yêu cầu học sinh xác định chính xác các hệ số a, b, c trong hàm số bậc hai đã cho. Đây là bước quan trọng để phân tích và vẽ đồ thị hàm số.
Ví dụ: Cho hàm số y = 2x2 - 5x + 3. Xác định a, b, c.
Giải: a = 2, b = -5, c = 3.
Bài 2: Tìm đỉnh và trục đối xứng của parabol
Sử dụng công thức tính đỉnh và trục đối xứng để xác định các yếu tố quan trọng của đồ thị hàm số. Việc này giúp học sinh hiểu rõ hình dạng và vị trí của parabol.
Ví dụ: Tìm đỉnh và trục đối xứng của parabol y = x2 - 4x + 3.
Giải: a = 1, b = -4, c = 3. x0 = -(-4)/(2*1) = 2. y0 = -( (-4)2 - 4*1*3 ) / (4*1) = -1. Vậy đỉnh là I(2; -1) và trục đối xứng là x = 2.
Bài 3: Vẽ đồ thị hàm số
Dựa vào các yếu tố đã tìm được (đỉnh, trục đối xứng, giao điểm với trục tọa độ), học sinh vẽ đồ thị hàm số một cách chính xác.
Mẹo học tập hiệu quả
- Nắm vững định nghĩa và tính chất: Đây là nền tảng để giải quyết mọi bài toán.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng công cụ hỗ trợ: Các phần mềm vẽ đồ thị hoặc máy tính bỏ túi có chức năng vẽ đồ thị có thể giúp bạn kiểm tra kết quả và hiểu rõ hơn về đồ thị hàm số.
- Tham khảo các nguồn tài liệu khác: Sách tham khảo, bài giảng trực tuyến, video hướng dẫn có thể cung cấp thêm kiến thức và phương pháp giải bài tập.
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn trong việc học tập môn Toán 12. Chúc các em học tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem chi tiết ở trên |
| Bài 2 | Xem chi tiết ở trên |