Giải Bài Tập 4.43 Trang 39 Toán 12 Tập 2

Giải bài tập 4.43 trang 39 SGK Toán 12 tập 2 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 4.43 trang 39 SGK Toán 12 tập 2. Bài tập này thuộc chương trình học về Đạo hàm của hàm số.

tusach.vn sẽ giúp các em hiểu rõ phương pháp giải và nắm vững kiến thức cần thiết để giải quyết các bài toán tương tự.

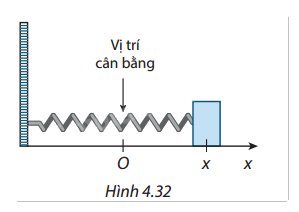
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát có vận tốc tại thời điểm \(t\) giây là \(v = 4\cos (t)\) (cm/s). Tìm li độ của con lắc tại thời điểm \(t = \frac{{2\pi }}{3}\) giây, biết khi \(t = \frac{\pi }{2}\) giây thì con lắc có li độ \(x = 4\) cm.

Đề bài

Giải bài tập 4.43 trang 39 SGK Toán 12 tập 2 - Cùng khám phá 1

A. \(\sqrt 3 \)cm.

B. 2 cm.

C. \(2\sqrt 3 \) cm.

D. 4 cm.

Phương pháp giải - Xem chi tiết Giải bài tập 4.43 trang 39 SGK Toán 12 tập 2 - Cùng khám phá 2

Chúng ta có thể sử dụng phương trình tích phân để tính li độ tại thời điểm \(t = \frac{{2\pi }}{3}\).

\(x\left( {\frac{{2\pi }}{3}} \right) - x\left( {\frac{\pi }{2}} \right) = \int_{\frac{\pi }{2}}^{\frac{{2\pi }}{3}} v (t){\mkern 1mu} dt\)

Trong đó, \(v(t) = 4\cos (t)\) là phương trình vận tốc của con lắc.

Lời giải chi tiết

Tính tích phân của \(4\cos (t)\):

\(\int 4 \cos (t){\mkern 1mu} dt = 4\sin (t)\)

Áp dụng cận tích phân từ \(\frac{\pi }{2}\) đến \(\frac{{2\pi }}{3}\):

\(x\left( {\frac{{2\pi }}{3}} \right) - x\left( {\frac{\pi }{2}} \right) = 4\left( {\sin \left( {\frac{{2\pi }}{3}} \right) - \sin \left( {\frac{\pi }{2}} \right)} \right) = 4\left( {\frac{{\sqrt 3 }}{2} - 1} \right) = 2\sqrt 3 - 4\)

Tính \(x\left( {\frac{{2\pi }}{3}} \right)\). Ta biết rằng \(x\left( {\frac{\pi }{2}} \right) = 4\), do đó:

\(x\left( {\frac{{2\pi }}{3}} \right) = x\left( {\frac{\pi }{2}} \right) + \left( {2\sqrt 3 - 4} \right)\)

\(x\left( {\frac{{2\pi }}{3}} \right) = 4 + 2\sqrt 3 - 4 = 2\sqrt 3 \)

Li độ của con lắc tại thời điểm \(t = \frac{{2\pi }}{3}\) giây là \(2\sqrt 3 \) cm.

Giải Bài Tập 4.43 Trang 39 Toán 12 Tập 2: Đạo Hàm và Ứng Dụng

Bài tập 4.43 trang 39 SGK Toán 12 tập 2 yêu cầu chúng ta vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế. Bài toán này thường liên quan đến việc tìm đạo hàm của hàm số, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, và tìm cực trị của hàm số.

Nội Dung Bài Tập 4.43

Để bắt đầu, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài tập 4.43 sẽ cho một hàm số và yêu cầu chúng ta thực hiện một trong các công việc sau:

Tính đạo hàm của hàm số.
Tìm các điểm cực trị của hàm số.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Giải một bài toán tối ưu hóa liên quan đến hàm số.

Phương Pháp Giải Bài Tập 4.43

Để giải bài tập 4.43 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:

Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và các đạo hàm đặc biệt (đạo hàm của hàm lượng giác, hàm mũ, hàm logarit).
Điều kiện cực trị: Một điểm x₀ được gọi là điểm cực trị của hàm số f(x) nếu f'(x₀) = 0 và f'(x) đổi dấu khi x đi qua x₀.
Khoảng đồng biến, nghịch biến: Hàm số f(x) đồng biến trên khoảng (a, b) nếu f'(x) > 0 với mọi x thuộc (a, b). Hàm số f(x) nghịch biến trên khoảng (a, b) nếu f'(x) < 0 với mọi x thuộc (a, b).

Lời Giải Chi Tiết Bài Tập 4.43 (Ví dụ)

Giả sử bài tập 4.43 có nội dung như sau:

Cho hàm số y = x³ - 3x² + 2. Tìm các điểm cực trị của hàm số.

Lời giải:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm cực trị: Giải phương trình y' = 0, ta được 3x² - 6x = 0 => x = 0 hoặc x = 2.
Xác định loại cực trị:
- Với x < 0: y' > 0 => Hàm số đồng biến.
- Với 0 < x < 2: y' < 0 => Hàm số nghịch biến.
- Với x > 2: y' > 0 => Hàm số đồng biến.
Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Tính giá trị cực trị:
- y(0) = 2 => Điểm cực đại là (0, 2).
- y(2) = -2 => Điểm cực tiểu là (2, -2).

Lưu Ý Khi Giải Bài Tập 4.43

Để đạt kết quả tốt nhất khi giải bài tập 4.43, các em cần:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Nắm vững các quy tắc tính đạo hàm và điều kiện cực trị.
Kiểm tra lại kết quả sau khi giải xong.
Luyện tập thường xuyên để nâng cao kỹ năng giải toán.

Tổng Kết

Bài tập 4.43 trang 39 SGK Toán 12 tập 2 là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự.

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. tusach.vn luôn sẵn sàng hỗ trợ các em!