Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 1.25 trang 35 SGK Toán 12 tập 1 - Cùng khám phá
SGK Toán 12 - Cùng khám phá
Giải Toán 12 tập 1 - Cùng khám phá
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 4. Khảo sát và vẽ đồ thị hàm số

Giải bài tập 1.25 trang 35 SGK Toán 12 tập 1 - Cùng khám phá

Giải Bài Tập 1.25 Trang 35 SGK Toán 12 Tập 1

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.25 trang 35 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập.

Chúng tôi sẽ cung cấp lời giải bài tập một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.

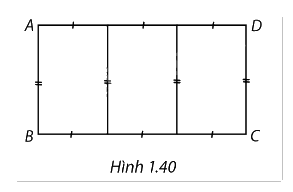
Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 600 m². Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình 1.40). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60.000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài và chiều rộng của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm).

Đề bài

Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 600 m². Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình 1.40). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60.000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài và chiều rộng của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm).

Giải bài tập 1.25 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiếtGiải bài tập 1.25 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 2

- Đặt chiều dài là 𝑥 và chiều rộng là 𝑦 của hình chữ nhật ABCD.

- Tính chi phí xây dựng hàng rào dựa trên chiều dài và chiều rộng.

- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.

- Sử dụng đạo hàm để tìm giá trị tối ưu.

Lời giải chi tiết

Gọi chiều dài là \(x\) \((0 < x \le 60)\) và chiều rộng là \(y\) \((0 < y \le x)\) của hình chữ nhật ABCD.

Diện tích của hình chữ nhật ABCD là: \(xy = 600\)

- Chi phí hàng rào ngoài là 2x+2y.

- Chi phí hàng rào bên trong là 2y.

-Tổng chi phí là: \(C = 60.000 \times (2x + 4y)\)

Viết hàm mục tiêu:

\(C = 60.000 \times \left( {2x + 4 \cdot \frac{{600}}{x}} \right) = 120.000 \times \left( {x + \frac{{1200}}{x}} \right)\)

Tìm giá trị cực trị: \(f(x) = x + \frac{{1200}}{x}\)

- Tính đạo hàm: \(f'(x) = 1 - \frac{{1200}}{{{x^2}}}\)

- Cho đạo hàm bằng 0: \(1 - \frac{{1200}}{{{x^2}}} = 0 \Rightarrow {x^2} = 1200 \Rightarrow x = \sqrt {1200} \approx 34,64(\;{\rm{m}})\)

Bảng biến thiên:

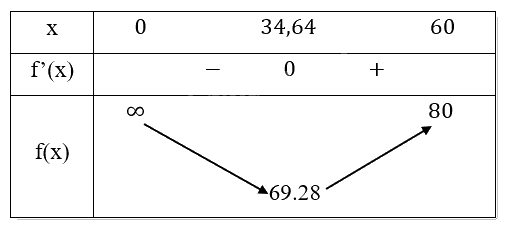
Giải bài tập 1.25 trang 35 SGK Toán 12 tập 1 - Cùng khám phá 3

Nhận thấy tại vị trí x=34,64 thì giá trị của f(x) là nhỏ nhất

Tính \(y\): \(y = \frac{{600}}{x} \approx \frac{{600}}{{34,64}} \approx 17,32(\;{\rm{m}})\)

Tính chi phí:

\(L = 2x + 4y = 2.34,64 + 4.17,32 \approx 138,56m\)

\(C = 60000 \times 135,56 \approx 8313600\)

Kết luận: Để chi phí xây dựng hàng rào là thấp nhất thì

- Chiều dài của hình chữ nhật ABCD: \(x \approx 34,64\)m

- Chiều rộng của hình chữ nhật ABCD: \(y \approx 17,32\)m

- Tổng chi phí xây dựng hàng rào: 8313600 đồng.

Giải Bài Tập 1.25 Trang 35 SGK Toán 12 Tập 1: Hướng Dẫn Chi Tiết

Bài tập 1.25 trang 35 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:

  1. Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
  2. Tính đạo hàm bậc nhất: Tính f'(x) để tìm các điểm dừng (điểm mà f'(x) = 0 hoặc không xác định).
  3. Lập bảng biến thiên: Xác định dấu của f'(x) trên các khoảng xác định để xác định khoảng hàm số đồng biến, nghịch biến.
  4. Tìm cực trị: Sử dụng dấu của f'(x) để xác định các điểm cực đại, cực tiểu.
  5. Khảo sát giới hạn: Tính giới hạn của hàm số khi x tiến tới vô cùng và các điểm gián đoạn.
  6. Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập để vẽ đồ thị hàm số.

Lời Giải Chi Tiết Bài Tập 1.25

Để minh họa, chúng ta sẽ cùng giải bài tập 1.25 cụ thể (giả sử bài tập là hàm số y = x3 - 3x2 + 2):

  1. Tập xác định: Hàm số xác định trên R.
  2. Đạo hàm bậc nhất: y' = 3x2 - 6x
  3. Tìm điểm dừng: 3x2 - 6x = 0 => x = 0 hoặc x = 2
  4. Bảng biến thiên:
    x-∞02+∞
    y'+-+
    y↗↘↗
  5. Cực trị:
    • Tại x = 0, y' đổi dấu từ dương sang âm => Hàm số đạt cực đại tại x = 0, ymax = 2
    • Tại x = 2, y' đổi dấu từ âm sang dương => Hàm số đạt cực tiểu tại x = 2, ymin = -2

Mẹo Giải Toán 12 Hiệu Quả

  • Nắm vững lý thuyết: Hiểu rõ các định nghĩa, định lý và công thức liên quan đến đạo hàm và ứng dụng của đạo hàm.
  • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
  • Sử dụng công cụ hỗ trợ: Sử dụng máy tính bỏ túi hoặc các phần mềm toán học để kiểm tra kết quả và vẽ đồ thị hàm số.
  • Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè.

Tusach.vn – Đồng Hành Cùng Bạn Học Toán 12

Tusach.vn là địa chỉ tin cậy cung cấp lời giải bài tập Toán 12 chính xác, chi tiết và dễ hiểu. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các phương pháp giải toán hiệu quả. Hãy truy cập Tusach.vn để học Toán 12 một cách hiệu quả nhất!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN