Giải mục 1 trang 97, 98, 99 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 97, 98, 99 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 97, 98, 99 SGK Toán 12 tập 2 tại tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn bộ giải bài tập Toán 12 tập 2 đầy đủ và chính xác.
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II". a) Hoàn thành sơ đồ hình cây sau:
LT2
Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 12 Cùng khám phá
Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.
Phương pháp giải:
- Sử dụng công thức xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\)
- Xác định tỉ lệ dân số nam và nữ
- Biết tỉ lệ mắc bệnh của từng giới
- Giải phương trình để tìm tỉ lệ nam mắc bệnh
Lời giải chi tiết:
* Xác định các biến cố:
\(A\): Biến cố là nam giới
\(B\): Biến cố là nữ giới
\(C\): Biến cố mắc bệnh bạch tạng
* Theo đề bài ta có các xác suất
\(P(A) = \frac{2}{5}\) ,\(P(B) = \frac{3}{5}\) ,\(P(C) = 0,45\% \),\(P(C|B) = 0,35\% \)
* Áp dụng công thức toàn phần
\(P(C) = P(A) \cdot P(C|A) + P(B) \cdot P(C|B)\)
\(0,45\% = (\frac{2}{5} \cdot P(C|A)) + (\frac{3}{5} \cdot 0,35\% )\)
* Giải Phương Trình
\(0,45\% = \frac{2}{5} \cdot P(C|A) + 0,21\% \)
\(0,45\% - 0,21\% = \frac{2}{5} \cdot P(C|A)\)
\(0,24\% = \frac{2}{5} \cdot P(C|A)\)
* Tính Tỉ Lệ Nam Mắc Bệnh
\(P(C|A) = \frac{{0,24\% \cdot 5}}{2}\)
\(P(C|A) = 0,6\% \)
Vậy tỉ lệ nam giới mắc bệnh bạch tạng là \(0,6\% \)
LT1
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.
Phương pháp giải:
Sử dụng công thức tính xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\).
Lời giải chi tiết:
* Các biến cố:
\(A\): Biến cố lấy quả trắng lần đầu
\(\bar A\): Biến cố lấy quả đen lần đầu
\(B\): Biến cố lấy quả trắng lần thứ hai
Xác suất ban đầu:
\(P(A) = \frac{5}{{15}} = \frac{1}{3}\)
\(P(\bar A) = \frac{{10}}{{15}} = \frac{2}{3}\)
* Xác suất có điều kiện:
\(P(B|A) = \frac{4}{{14}} = \frac{2}{7}\)
\(P(B|\bar A) = \frac{5}{{14}}\)
* Công thức xác suất toàn phần: \(P(B) = P(A) \cdot P(B|A) + P(\bar A) \cdot P(B|\bar A)\)
Thay số: \(P(B) = \left( {\frac{1}{3} \cdot \frac{2}{7}} \right) + \left( {\frac{2}{3} \cdot \frac{5}{{14}}} \right) = \frac{2}{{21}} + \frac{{10}}{{42}} = \frac{2}{{21}} + \frac{5}{{21}} = \frac{7}{{21}} = \frac{1}{3}\)
Vậy xác suất lấy được quả cầu trắng lần thứ hai là: \(P(B) = \frac{1}{3}\)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cùng khám phá
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II".
a) Hoàn thành sơ đồ hình cây sau:
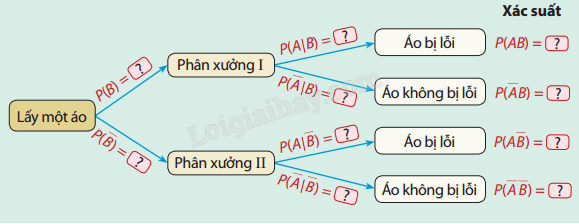
b) Ta nhận thấy biến cố A: "Lấy được áo bị lỗi" có thể xảy ra đồng thời với biến cố B: "Áo được sản xuất bởi phân xưởng I" hoặc biến cố B: "Áo được sản xuất bởi phân xưởng II". Người ta chứng minh được rằng: \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\). Hãy tính xác suất lấy được áo bị lỗi trong lô hàng.
Phương pháp giải:
a) Sử dụng công thức \(P(B|A) = \frac{{P(AB)}}{{P(A)}}\) hoặc \(P(AB) = P(B|A).P(A)\).
b) Sử dụng kết quả ở câu a và áp dụng công thức \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\) để tính xác suất.
Lời giải chi tiết:
a)
- Xác suất phân xưởng I sản xuất áo: \(P(B) = 0,4\)
- Xác suất phân xưởng II sản xuất áo: \(P(\bar B) = 0,6\)
- Xác suất áo bị lỗi từ phân xưởng I: \(P(A|B) = 0,02\)
- Xác suất áo bị lỗi từ phân xưởng II: \(P(A|\bar B) = 0.03\)
- Xác suất áo không bị lỗi từ phân xưởng I và phân xưởng II
Áo không bị lỗi từ phân xưởng I: \(P(\bar A|B) = 1 - P(A|B) \Leftrightarrow P(\bar A|B) = 1 - 0,02 = 0,98\)
Áo không bị lỗi từ phân xưởng II: \(P(\bar A|\bar B) = 1 - P(A|\bar B) \Leftrightarrow P(\bar A|\bar B) = 1 - 0.03 = 0,97\)
- Xác suất \(P(AB)\): Là xác suất áo bị lỗi và thuộc phân xưởng I
\(P(AB) = P(A|B) \cdot P(B) \Leftrightarrow P(AB) = 0,02 \cdot 0,4 = 0,008\)
- Xác suất \(P(\bar AB)\): Là xác suất áo không bị lỗi và thuộc phân xưởng I
\(P(\bar AB) = P(\bar A|B) \cdot P(B) \Leftrightarrow P(\bar AB) = 0,98 \cdot 0,4 = 0,392\)
- Xác suất \(P(A\bar B)\): Là xác suất áo bị lỗi và thuộc phân xưởng II
\(P(A\bar B) = P(A|\bar B) \cdot P(\bar B) \Leftrightarrow P(A\bar B) = 0,03 \cdot 0,6 = 0,018\)
- Xác suất \(P(\bar A\bar B)\): Là xác suất áo không bị lỗi và thuộc phân xưởng II
\(P(\bar A\bar B) = P(\bar A|\bar B) \cdot P(\bar B) \Leftrightarrow P(\bar A\bar B) = 0,97 \cdot 0,6 = 0,582\)
b)
Xác suất lấy được áo bị lỗi trong lô hàng là:
\(P(A) = P(AB) + P(A\bar B) = 0,008 + 0,018 = 0,026\)
- HĐ1
- LT1
- LT2
Trả lời câu hỏi Hoạt động 1 trang 97 SGK Toán 12 Cùng khám phá
Hai phân xưởng I, II cùng sản xuất một lô áo với số sản phẩm chiếm tỉ lệ lần lượt là 40% và 60%. Thông qua dữ liệu thống kê có từ trước, người ta thấy rằng tỉ lệ áo bị lỗi của các phân xưởng I, II tương ứng là 2% và 3%. Lấy ngẫu nhiên một chiếc áo trong lô hàng. Gọi A là biến cố "Lấy được áo bị lỗi" và B, \(\overline B \) lần lượt là các biến cố "Lấy được áo từ phân xưởng I" và "Lấy được áo từ phân xưởng II".
a) Hoàn thành sơ đồ hình cây sau:
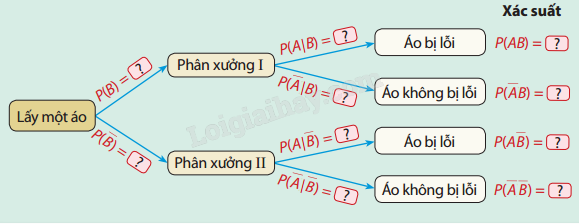
b) Ta nhận thấy biến cố A: "Lấy được áo bị lỗi" có thể xảy ra đồng thời với biến cố B: "Áo được sản xuất bởi phân xưởng I" hoặc biến cố B: "Áo được sản xuất bởi phân xưởng II". Người ta chứng minh được rằng: \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\). Hãy tính xác suất lấy được áo bị lỗi trong lô hàng.
Phương pháp giải:
a) Sử dụng công thức \(P(B|A) = \frac{{P(AB)}}{{P(A)}}\) hoặc \(P(AB) = P(B|A).P(A)\).
b) Sử dụng kết quả ở câu a và áp dụng công thức \(P\left( A \right){\rm{ }} = {\rm{ }}P\left( {AB} \right){\rm{ }} + {\rm{ }}P\left( {A\overline B } \right)\) để tính xác suất.
Lời giải chi tiết:
a)
- Xác suất phân xưởng I sản xuất áo: \(P(B) = 0,4\)
- Xác suất phân xưởng II sản xuất áo: \(P(\bar B) = 0,6\)
- Xác suất áo bị lỗi từ phân xưởng I: \(P(A|B) = 0,02\)
- Xác suất áo bị lỗi từ phân xưởng II: \(P(A|\bar B) = 0.03\)
- Xác suất áo không bị lỗi từ phân xưởng I và phân xưởng II
Áo không bị lỗi từ phân xưởng I: \(P(\bar A|B) = 1 - P(A|B) \Leftrightarrow P(\bar A|B) = 1 - 0,02 = 0,98\)
Áo không bị lỗi từ phân xưởng II: \(P(\bar A|\bar B) = 1 - P(A|\bar B) \Leftrightarrow P(\bar A|\bar B) = 1 - 0.03 = 0,97\)
- Xác suất \(P(AB)\): Là xác suất áo bị lỗi và thuộc phân xưởng I
\(P(AB) = P(A|B) \cdot P(B) \Leftrightarrow P(AB) = 0,02 \cdot 0,4 = 0,008\)
- Xác suất \(P(\bar AB)\): Là xác suất áo không bị lỗi và thuộc phân xưởng I
\(P(\bar AB) = P(\bar A|B) \cdot P(B) \Leftrightarrow P(\bar AB) = 0,98 \cdot 0,4 = 0,392\)
- Xác suất \(P(A\bar B)\): Là xác suất áo bị lỗi và thuộc phân xưởng II
\(P(A\bar B) = P(A|\bar B) \cdot P(\bar B) \Leftrightarrow P(A\bar B) = 0,03 \cdot 0,6 = 0,018\)
- Xác suất \(P(\bar A\bar B)\): Là xác suất áo không bị lỗi và thuộc phân xưởng II
\(P(\bar A\bar B) = P(\bar A|\bar B) \cdot P(\bar B) \Leftrightarrow P(\bar A\bar B) = 0,97 \cdot 0,6 = 0,582\)
b)
Xác suất lấy được áo bị lỗi trong lô hàng là:
\(P(A) = P(AB) + P(A\bar B) = 0,008 + 0,018 = 0,026\)
Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 12 Cùng khám phá
Một hộp có 5 quả cầu trắng và 10 quả cầu đen cùng kích thước và khối lượng. Lấy ngẫu nhiên lần lượt hai quả cầu (không hoàn lại) từ hộp. Tính xác suất để lần thứ hai lấy được quả cầu trắng.
Phương pháp giải:
Sử dụng công thức tính xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\).
Lời giải chi tiết:
* Các biến cố:
\(A\): Biến cố lấy quả trắng lần đầu
\(\bar A\): Biến cố lấy quả đen lần đầu
\(B\): Biến cố lấy quả trắng lần thứ hai
Xác suất ban đầu:
\(P(A) = \frac{5}{{15}} = \frac{1}{3}\)
\(P(\bar A) = \frac{{10}}{{15}} = \frac{2}{3}\)
* Xác suất có điều kiện:
\(P(B|A) = \frac{4}{{14}} = \frac{2}{7}\)
\(P(B|\bar A) = \frac{5}{{14}}\)
* Công thức xác suất toàn phần: \(P(B) = P(A) \cdot P(B|A) + P(\bar A) \cdot P(B|\bar A)\)
Thay số: \(P(B) = \left( {\frac{1}{3} \cdot \frac{2}{7}} \right) + \left( {\frac{2}{3} \cdot \frac{5}{{14}}} \right) = \frac{2}{{21}} + \frac{{10}}{{42}} = \frac{2}{{21}} + \frac{5}{{21}} = \frac{7}{{21}} = \frac{1}{3}\)
Vậy xác suất lấy được quả cầu trắng lần thứ hai là: \(P(B) = \frac{1}{3}\)
Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 12 Cùng khám phá
Ở một địa phương, tỉ lệ nam và nữ là 2:3. Số người mắc bệnh bạch tạng của địa phương này chiếm tỉ lệ 0,45% dân cư. Tính tỉ lệ nam giới mắc bệnh bạch tạng của địa phương đó, biết tỉ lệ này ở nữ là 0,35%.
Phương pháp giải:
- Sử dụng công thức xác suất toàn phần: \(P(A) = P(B).P(A|B) + P(\bar B).P(A|\bar B)\)
- Xác định tỉ lệ dân số nam và nữ
- Biết tỉ lệ mắc bệnh của từng giới
- Giải phương trình để tìm tỉ lệ nam mắc bệnh
Lời giải chi tiết:
* Xác định các biến cố:
\(A\): Biến cố là nam giới
\(B\): Biến cố là nữ giới
\(C\): Biến cố mắc bệnh bạch tạng
* Theo đề bài ta có các xác suất
\(P(A) = \frac{2}{5}\) ,\(P(B) = \frac{3}{5}\) ,\(P(C) = 0,45\% \),\(P(C|B) = 0,35\% \)
* Áp dụng công thức toàn phần
\(P(C) = P(A) \cdot P(C|A) + P(B) \cdot P(C|B)\)
\(0,45\% = (\frac{2}{5} \cdot P(C|A)) + (\frac{3}{5} \cdot 0,35\% )\)
* Giải Phương Trình
\(0,45\% = \frac{2}{5} \cdot P(C|A) + 0,21\% \)
\(0,45\% - 0,21\% = \frac{2}{5} \cdot P(C|A)\)
\(0,24\% = \frac{2}{5} \cdot P(C|A)\)
* Tính Tỉ Lệ Nam Mắc Bệnh
\(P(C|A) = \frac{{0,24\% \cdot 5}}{2}\)
\(P(C|A) = 0,6\% \)
Vậy tỉ lệ nam giới mắc bệnh bạch tạng là \(0,6\% \)
Giải mục 1 trang 97, 98, 99 SGK Toán 12 tập 2: Tổng quan và Phương pháp giải
Mục 1 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về Đạo hàm của hàm số lượng giác và Ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức nền tảng về đạo hàm là vô cùng quan trọng để giải quyết các bài tập trong mục này. Tusach.vn sẽ cung cấp cho bạn lời giải chi tiết từng bài tập, kèm theo các lưu ý quan trọng và phương pháp giải hiệu quả.
Nội dung chính của mục 1 trang 97, 98, 99 SGK Toán 12 tập 2
- Bài 1: Tính đạo hàm của các hàm số lượng giác cơ bản (sin x, cos x, tan x, cot x).
- Bài 2: Áp dụng các quy tắc tính đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp) để tính đạo hàm của các hàm số phức tạp hơn.
- Bài 3: Sử dụng đạo hàm để tìm cực trị của hàm số.
- Bài 4: Khảo sát sự biến thiên của hàm số bằng cách xét dấu đạo hàm.
- Bài 5: Giải các bài toán thực tế liên quan đến ứng dụng của đạo hàm.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 1:
Ví dụ 1: Tính đạo hàm của hàm số y = sin(2x + 1)
Giải:
Sử dụng quy tắc hàm hợp, ta có:
y' = cos(2x + 1) * (2x + 1)' = 2cos(2x + 1)
Ví dụ 2: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Giải:
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 và x = 2
- Tính đạo hàm bậc hai: y'' = 6x - 6
- Xác định cực trị:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Lưu ý quan trọng khi giải bài tập
Để giải quyết các bài tập trong mục 1 một cách hiệu quả, bạn cần lưu ý những điều sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Thành thạo các quy tắc tính đạo hàm.
- Hiểu rõ ý nghĩa của đạo hàm trong việc khảo sát hàm số.
- Luyện tập thường xuyên để rèn luyện kỹ năng giải bài tập.
Tại sao nên chọn tusach.vn để học Toán 12?
Tusach.vn tự hào là một trong những website cung cấp tài liệu học tập Toán 12 uy tín và chất lượng nhất hiện nay. Chúng tôi cam kết:
- Lời giải chi tiết, dễ hiểu, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
- Cập nhật liên tục các bài tập mới và đáp án chính xác.
- Giao diện thân thiện, dễ sử dụng.
- Hỗ trợ học tập 24/7.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác và cùng chúng tôi chinh phục môn Toán 12!
| Chủ đề | Mức độ khó |
|---|---|
| Đạo hàm lượng giác | Trung bình |
| Khảo sát hàm số | Khó |