Giải mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2. Tại tusach.vn, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu nhất để hỗ trợ các em trong quá trình học tập.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, không chỉ đơn thuần là học thuộc đáp án.
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số (y = x - 3), trục hoành và các đường thẳng (x = 1) và (x = 6).
LT1
Trả lời câu hỏi Luyện tập 1 trang 23 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và các đường thẳng \(x = - 3,x = 2\).
Phương pháp giải:
- Xác định ình phẳng cần tính diện tích.
- Phân tích dấu của hàm \(y = {x^3}\).
- Tìm biểu thức diện tích tổng quát.
- Tính các tích phân dựa trên biểu thức diện tích tổng quát.
Lời giải chi tiết:
Hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành \(y = 0\), và hai đường thẳng \(x = - 3\) và \(x = 2\). Tại các khoảng khác nhau, đồ thị có thể nằm bên trên hoặc bên dưới trục hoành, nên cần tính tích phân của giá trị tuyệt đối \(|{x^3}|\) để đảm bảo kết quả diện tích là dương.
- Từ \(x = - 3\) đến \(x = 0\), \(y = {x^3}\) là âm.
- Từ \(x = 0\) đến \(x = 2\), \(y = {x^3}\) là dương.
Diện tích hình phẳng được tính bằng cách lấy tích phân của \(|{x^3}|\) từ \(x = - 3\) đến \(x = 2\)
\(S = \int_{ - 3}^0 - {x^3}{\mkern 1mu} dx + \int_0^2 {{x^3}} {\mkern 1mu} dx\)
Trong khoảng \(x \in [ - 3,0]\), đổi dấu hàm số \({x^3}\) để đảm bảo diện tích là dương.
Tích phân của \( - {x^3}\) trong khoảng \([ - 3,0]\):
\(\int_{ - 3}^0 - {x^3}{\mkern 1mu} dx = - \left[ {\frac{{{x^4}}}{4}} \right]_{ - 3}^0 = - \left( {\frac{{{0^4}}}{4} - \frac{{{{( - 3)}^4}}}{4}} \right) = - \left( {0 - \frac{{81}}{4}} \right) = \frac{{81}}{4}\)
Tích phân của \({x^3}\) trong khoảng \(\left[ {0,{\rm{ }}2} \right]\):
\(\int_0^2 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_0^2 = \frac{{{2^4}}}{4} - \frac{{{0^4}}}{4} = \frac{{16}}{4} = 4\)
Diện tích tổng cộng là tổng của hai kết quả tích phân:
\(S = \frac{{81}}{4} + 4 = \frac{{81}}{4} + \frac{{16}}{4} = \frac{{97}}{4}\)
Vậy, diện tích của hình phẳng là:
\(S = \frac{{97}}{4} = 24.25\).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 22 SGK Toán 12 Cùng khám phá
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = x - 3\), trục hoành và các đường thẳng \(x = 1\) và \(x = 6\).
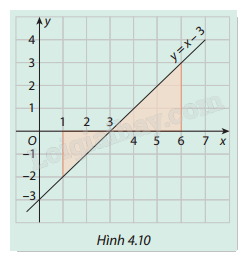
a) Tính diện tích của (H).
b) Tính các tích phân \(\int_1^6 {(x - 3)} {\mkern 1mu} dx\) và \(\int_1^6 | x - 3|{\mkern 1mu} dx\). So sánh hai tích phân này với kết quả tính được ở câu a và rút ra nhận xét.
Phương pháp giải:
a)
Diện tích (H) có thể tính bằng cách cộng diện tích của hai tam giác. Diện tích của tam giác được tính bằng công thức:
\(S = \frac{1}{2} \times h \times \)đáy
b)
- Tính trực tiếp các tích phân \(\int_1^6 {(x - 3)dx} \) và \(\int_1^6 {\left| {x - 3} \right|dx} \).
- So sánh kết quả của hai tích phân này với diện tích tính được ở câu a để rút ra nhận xét.
Lời giải chi tiết:
a)
Hình phẳng (H) trong đề bài là hai hình tam giác vuông, với các cạnh là:
- Đáy của tam giác thứ nhất: \(6 - 3 = 3\)
- Chiều cao của tam giác thứ nhất: \(3 - 0 = 3\)
- Đáy của tam giác thứ hai: \(3 - 1 = 2\)
- Chiều cao của tam giác thứ nhất: \(0 - ( - 2) = 2\)
Diện tích tam giác được tính theo công thức:
\(S = \frac{1}{2} \times 3 \times 3 + \frac{1}{2} \times 2 \times 2 = \frac{9}{2} + 2 = 6,5\)
b)
Tính tích phân thứ nhất:
\(\int_1^6 {(x - 3)} {\mkern 1mu} dx = \left[ {\frac{{{{(x - 3)}^2}}}{2}} \right]_1^6 = \frac{9}{2} - 2 = \frac{7}{2} = 2,5\)
Tính tích phân thứ hai:
\(\int_1^6 | x - 3|{\mkern 1mu} dx = \int_1^3 {(3 - x)} {\mkern 1mu} dx + \int_3^6 {(x - 3)} {\mkern 1mu} dx = 2 + \frac{9}{2} = 6,5\)
Nhận xét:
- Tích phân thứ nhất \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = 3.5\) không phản ánh diện tích thực của hình phẳng, vì hàm số nhận giá trị âm trong khoảng từ 1 đến 3.
- Tích phân thứ hai \(\int_1^6 | x - 3|{\mkern 1mu} dx = 6.5\) chính là diện tích hình phẳng tính được ở câu a, vì nó tính giá trị tuyệt đối của hàm số, tức là cả phần âm và phần dương.
LT2
Trả lời câu hỏi Luyện tập 2 trang 26 SGK Toán 12 Cùng khám phá
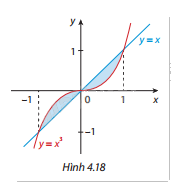
Tính diện tích hình phẳng được tô màu trong Hình 4.18.
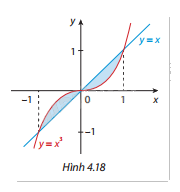
Phương pháp giải:
- Xác định giao điểm của hai đường \(y = {x^3}\) và \(y = x\) bằng cách giải phương trình: \({x^3} = x\)
- Diện tích hình phẳng giữa hai đường cong \(y = {x^3}\) và \(y = x\) trong khoảng từ \(x = - 1\) đến \(x = 1\) được tính bằng:
\(S = \int_{ - 1}^1 | x - {x^3}|{\mkern 1mu} dx\)
Lời giải chi tiết:
Giao điểm của hai đường \(y = {x^3}\) và \(y = x\) là:
\({x^3} = x \Leftrightarrow x({x^2} - 1) = 0\)
Suy ra: \(x = 0\), \(x = 1\), và \(x = - 1\).
Vì trên khoảng từ \( - 1\) đến 0, \(y = {x^3}\) nằm trên \(y = x\), và trên khoảng từ 0 đến 1, \(y = x\) nằm trên \(y = {x^3}\), ta có:
\(S = \int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx + \int_0^1 {(x - {x^3})} {\mkern 1mu} dx\)
Tính tích phân:
\(\int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right]_{ - 1}^0 = \left( {0 - 0} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) = - \frac{1}{4} + \frac{1}{2} = \frac{1}{4}\)
\(\int_0^1 {(x - {x^3})} {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{4}} \right]_0^1 = \left( {\frac{1}{2} - \frac{1}{4}} \right) - (0 - 0) = \frac{1}{4}\)
Vậy diện tích hình phẳng là:
\(S = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 24 SGK Toán 12 Cùng khám phá
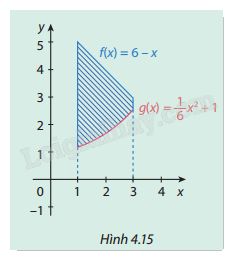
Cho hai hàm số \(f(x) = 6 - x\), \(g(x) = \frac{1}{6}{x^2} + 1\).
a) Tính \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = f\left( x \right).\)
b) Tính \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = g\left( x \right).\)
c) Qua \({S_1},\,\,{S_2}\) tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
\(y = f\left( x \right),{\rm{ }}y = g\left( x \right)\) và các đường thẳng \(x = 1,{\rm{ }}x = 3\). (phần hình phẳng được gạch chéo trong Hình 4.15).
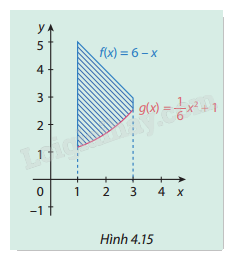
Phương pháp giải:
a) Tính diện tích \({S_1}\) bằng cách lấy tích phân của hàm số \(f(x) = 6 - x\) từ \(x = 1\) đến \(x = 3\)
b) Tính diện tích \({S_2}\) bằng cách lấy tích phân của hàm số \(g(x) = \frac{1}{6}{x^2} + 1\) từ \(x = 1\) đến \(x = 3\).
c) Tính diện tích hình phẳng giới hạn bởi hai đồ thị bằng cách lấy hiệu diện tích \({S_1} - {S_2}\).
Lời giải chi tiết:
a) Tính \({S_1}\)
Diện tích \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = f(x)\):
\({S_1} = \int_1^3 {(6 - x)} dx\)
Tính tích phân:
\({S_1} = \left[ {6x - \frac{{{x^2}}}{2}} \right]_1^3\)
\({S_1} = \left( {6 \cdot 3 - \frac{{{3^2}}}{2}} \right) - \left( {6 \cdot 1 - \frac{{{1^2}}}{2}} \right)\)
\({S_1} = (18 - 4.5) - (6 - 0.5) = 13.5 - 5.5 = 8\)
b) Tính \({S_2}\)
Diện tích \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = g(x)\):
\({S_2} = \int_1^3 {\left( {\frac{1}{6}{x^2} + 1} \right)} dx\)
Tính tích phân:
\({S_2} = \left[ {\frac{1}{6} \cdot \frac{{{x^3}}}{3} + x} \right]_1^3\)
\({S_2} = \left( {\frac{1}{6} \cdot \frac{{27}}{3} + 3} \right) - \left( {\frac{1}{6} \cdot \frac{1}{3} + 1} \right)\)
\({S_2} = \left( {\frac{9}{6} + 3} \right) - \left( {\frac{1}{{18}} + 1} \right)\)
\({S_2} = (1.5 + 3) - \left( {\frac{1}{{18}} + 1} \right) = 4.5 - \frac{{19}}{{18}} = \frac{{81}}{{18}} - \frac{{19}}{{18}} = \frac{{62}}{{18}} \approx 3,44\)
c) Tính diện tích hình phẳng giữa hai đồ thị
Diện tích hình phẳng giới hạn bởi hai đồ thị \(f(x)\) và \(g(x)\) trong khoảng \(x = 1\) đến \(x = 3\) là:
\(S = {S_1} - {S_2} = 8 - 3,44 = 4,56\)
Vậy, diện tích hình phẳng giữa hai đồ thị là \(S = 4,56\).
VD1
Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Cùng khám phá
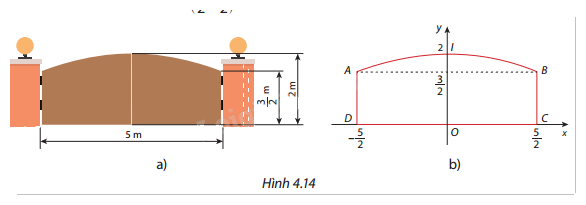
Một cái cổng có kích thước như Hình 4.14a. Vòm cổng có hình dạng một parabol có đỉnh \(I(0;2)\) và đi qua điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) như Hình 4.14b. Tính diện tích hai cánh cửa cổng.
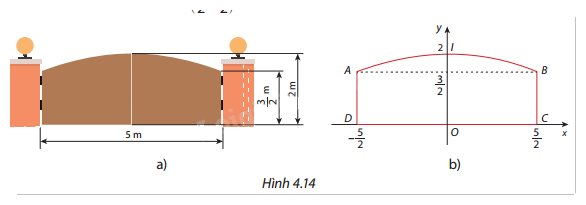
Phương pháp giải:
- Xác định phương trình parabol.
- Tính diện tích một cánh cửa cổng bằng cách tính tích phân diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\).
- Nhân diện tích một cánh cửa với 2 để ra diện tích hai cánh cửa cổng.
Lời giải chi tiết:
Xác định phương trình parabol đỉnh \(I(0;2)\) có dạng:
\(y = a{x^2} + 2\)
Sử dụng điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) để tìm hệ số \(a\):
\(\frac{3}{2} = a{\left( {\frac{5}{2}} \right)^2} + 2\)
Giải ra ta được:
\(a = - \frac{2}{{25}}\)
Vậy phương trình của parabol là:
\(y = - \frac{2}{{25}}{x^2} + 2\)
Diện tích một cánh cửa là diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\), được tính bằng tích phân:
\(S = 2\int_0^{\frac{5}{2}} {\left( { - \frac{2}{{25}}{x^2} + 2} \right)} dx\)
Tính tích phân:
\(S = 2\left[ {\left( { - \frac{2}{{25}} \cdot \frac{{{x^3}}}{3} + 2x} \right)} \right]_0^{\frac{5}{2}}\)
\(S = 2\left[ { - \frac{2}{{25}} \cdot \frac{{125}}{{24}} + 2 \cdot \frac{5}{2}} \right]\)
\(S = 2\left( { - \frac{5}{{12}} + 5} \right) = 2\left( {\frac{{55}}{{12}}} \right) = \frac{{55}}{6}\)
Vậy, diện tích hai cánh cửa cổng là: \(9,167{{\rm{m}}^2}\).
- HĐ1
- LT1
- VD1
- HĐ2
- LT2
Trả lời câu hỏi Hoạt động 1 trang 22 SGK Toán 12 Cùng khám phá
Trong Hình 4.10, gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y = x - 3\), trục hoành và các đường thẳng \(x = 1\) và \(x = 6\).
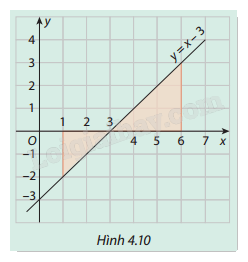
a) Tính diện tích của (H).
b) Tính các tích phân \(\int_1^6 {(x - 3)} {\mkern 1mu} dx\) và \(\int_1^6 | x - 3|{\mkern 1mu} dx\). So sánh hai tích phân này với kết quả tính được ở câu a và rút ra nhận xét.
Phương pháp giải:
a)
Diện tích (H) có thể tính bằng cách cộng diện tích của hai tam giác. Diện tích của tam giác được tính bằng công thức:
\(S = \frac{1}{2} \times h \times \)đáy
b)
- Tính trực tiếp các tích phân \(\int_1^6 {(x - 3)dx} \) và \(\int_1^6 {\left| {x - 3} \right|dx} \).
- So sánh kết quả của hai tích phân này với diện tích tính được ở câu a để rút ra nhận xét.
Lời giải chi tiết:
a)
Hình phẳng (H) trong đề bài là hai hình tam giác vuông, với các cạnh là:
- Đáy của tam giác thứ nhất: \(6 - 3 = 3\)
- Chiều cao của tam giác thứ nhất: \(3 - 0 = 3\)
- Đáy của tam giác thứ hai: \(3 - 1 = 2\)
- Chiều cao của tam giác thứ nhất: \(0 - ( - 2) = 2\)
Diện tích tam giác được tính theo công thức:
\(S = \frac{1}{2} \times 3 \times 3 + \frac{1}{2} \times 2 \times 2 = \frac{9}{2} + 2 = 6,5\)
b)
Tính tích phân thứ nhất:
\(\int_1^6 {(x - 3)} {\mkern 1mu} dx = \left[ {\frac{{{{(x - 3)}^2}}}{2}} \right]_1^6 = \frac{9}{2} - 2 = \frac{7}{2} = 2,5\)
Tính tích phân thứ hai:
\(\int_1^6 | x - 3|{\mkern 1mu} dx = \int_1^3 {(3 - x)} {\mkern 1mu} dx + \int_3^6 {(x - 3)} {\mkern 1mu} dx = 2 + \frac{9}{2} = 6,5\)
Nhận xét:
- Tích phân thứ nhất \(\int_1^6 {(x - 3)} {\mkern 1mu} dx = 3.5\) không phản ánh diện tích thực của hình phẳng, vì hàm số nhận giá trị âm trong khoảng từ 1 đến 3.
- Tích phân thứ hai \(\int_1^6 | x - 3|{\mkern 1mu} dx = 6.5\) chính là diện tích hình phẳng tính được ở câu a, vì nó tính giá trị tuyệt đối của hàm số, tức là cả phần âm và phần dương.
Trả lời câu hỏi Luyện tập 1 trang 23 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và các đường thẳng \(x = - 3,x = 2\).
Phương pháp giải:
- Xác định ình phẳng cần tính diện tích.
- Phân tích dấu của hàm \(y = {x^3}\).
- Tìm biểu thức diện tích tổng quát.
- Tính các tích phân dựa trên biểu thức diện tích tổng quát.
Lời giải chi tiết:
Hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành \(y = 0\), và hai đường thẳng \(x = - 3\) và \(x = 2\). Tại các khoảng khác nhau, đồ thị có thể nằm bên trên hoặc bên dưới trục hoành, nên cần tính tích phân của giá trị tuyệt đối \(|{x^3}|\) để đảm bảo kết quả diện tích là dương.
- Từ \(x = - 3\) đến \(x = 0\), \(y = {x^3}\) là âm.
- Từ \(x = 0\) đến \(x = 2\), \(y = {x^3}\) là dương.
Diện tích hình phẳng được tính bằng cách lấy tích phân của \(|{x^3}|\) từ \(x = - 3\) đến \(x = 2\)
\(S = \int_{ - 3}^0 - {x^3}{\mkern 1mu} dx + \int_0^2 {{x^3}} {\mkern 1mu} dx\)
Trong khoảng \(x \in [ - 3,0]\), đổi dấu hàm số \({x^3}\) để đảm bảo diện tích là dương.
Tích phân của \( - {x^3}\) trong khoảng \([ - 3,0]\):
\(\int_{ - 3}^0 - {x^3}{\mkern 1mu} dx = - \left[ {\frac{{{x^4}}}{4}} \right]_{ - 3}^0 = - \left( {\frac{{{0^4}}}{4} - \frac{{{{( - 3)}^4}}}{4}} \right) = - \left( {0 - \frac{{81}}{4}} \right) = \frac{{81}}{4}\)
Tích phân của \({x^3}\) trong khoảng \(\left[ {0,{\rm{ }}2} \right]\):
\(\int_0^2 {{x^3}} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4}} \right]_0^2 = \frac{{{2^4}}}{4} - \frac{{{0^4}}}{4} = \frac{{16}}{4} = 4\)
Diện tích tổng cộng là tổng của hai kết quả tích phân:
\(S = \frac{{81}}{4} + 4 = \frac{{81}}{4} + \frac{{16}}{4} = \frac{{97}}{4}\)
Vậy, diện tích của hình phẳng là:
\(S = \frac{{97}}{4} = 24.25\).
Trả lời câu hỏi Vận dụng 1 trang 24 SGK Toán 12 Cùng khám phá
Một cái cổng có kích thước như Hình 4.14a. Vòm cổng có hình dạng một parabol có đỉnh \(I(0;2)\) và đi qua điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) như Hình 4.14b. Tính diện tích hai cánh cửa cổng.
Phương pháp giải:
- Xác định phương trình parabol.
- Tính diện tích một cánh cửa cổng bằng cách tính tích phân diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\).
- Nhân diện tích một cánh cửa với 2 để ra diện tích hai cánh cửa cổng.
Lời giải chi tiết:
Xác định phương trình parabol đỉnh \(I(0;2)\) có dạng:
\(y = a{x^2} + 2\)
Sử dụng điểm \(B\left( {\frac{5}{2};\frac{3}{2}} \right)\) để tìm hệ số \(a\):
\(\frac{3}{2} = a{\left( {\frac{5}{2}} \right)^2} + 2\)
Giải ra ta được:
\(a = - \frac{2}{{25}}\)
Vậy phương trình của parabol là:
\(y = - \frac{2}{{25}}{x^2} + 2\)
Diện tích một cánh cửa là diện tích hình phẳng giới hạn bởi parabol và trục hoành trong khoảng từ \(x = 0\) đến \(x = \frac{5}{2}\), được tính bằng tích phân:
\(S = 2\int_0^{\frac{5}{2}} {\left( { - \frac{2}{{25}}{x^2} + 2} \right)} dx\)
Tính tích phân:
\(S = 2\left[ {\left( { - \frac{2}{{25}} \cdot \frac{{{x^3}}}{3} + 2x} \right)} \right]_0^{\frac{5}{2}}\)
\(S = 2\left[ { - \frac{2}{{25}} \cdot \frac{{125}}{{24}} + 2 \cdot \frac{5}{2}} \right]\)
\(S = 2\left( { - \frac{5}{{12}} + 5} \right) = 2\left( {\frac{{55}}{{12}}} \right) = \frac{{55}}{6}\)
Vậy, diện tích hai cánh cửa cổng là: \(9,167{{\rm{m}}^2}\).
Trả lời câu hỏi Hoạt động 2 trang 24 SGK Toán 12 Cùng khám phá
Cho hai hàm số \(f(x) = 6 - x\), \(g(x) = \frac{1}{6}{x^2} + 1\).
a) Tính \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = f\left( x \right).\)
b) Tính \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1,{\rm{ }}x = 3\) và đồ thị hàm số \(y = g\left( x \right).\)
c) Qua \({S_1},\,\,{S_2}\) tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
\(y = f\left( x \right),{\rm{ }}y = g\left( x \right)\) và các đường thẳng \(x = 1,{\rm{ }}x = 3\). (phần hình phẳng được gạch chéo trong Hình 4.15).
Phương pháp giải:
a) Tính diện tích \({S_1}\) bằng cách lấy tích phân của hàm số \(f(x) = 6 - x\) từ \(x = 1\) đến \(x = 3\)
b) Tính diện tích \({S_2}\) bằng cách lấy tích phân của hàm số \(g(x) = \frac{1}{6}{x^2} + 1\) từ \(x = 1\) đến \(x = 3\).
c) Tính diện tích hình phẳng giới hạn bởi hai đồ thị bằng cách lấy hiệu diện tích \({S_1} - {S_2}\).
Lời giải chi tiết:
a) Tính \({S_1}\)
Diện tích \({S_1}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = f(x)\):
\({S_1} = \int_1^3 {(6 - x)} dx\)
Tính tích phân:
\({S_1} = \left[ {6x - \frac{{{x^2}}}{2}} \right]_1^3\)
\({S_1} = \left( {6 \cdot 3 - \frac{{{3^2}}}{2}} \right) - \left( {6 \cdot 1 - \frac{{{1^2}}}{2}} \right)\)
\({S_1} = (18 - 4.5) - (6 - 0.5) = 13.5 - 5.5 = 8\)
b) Tính \({S_2}\)
Diện tích \({S_2}\) là diện tích hình phẳng giới hạn bởi trục hoành, hai đường thẳng \(x = 1\), \(x = 3\) và đồ thị hàm số \(y = g(x)\):
\({S_2} = \int_1^3 {\left( {\frac{1}{6}{x^2} + 1} \right)} dx\)
Tính tích phân:
\({S_2} = \left[ {\frac{1}{6} \cdot \frac{{{x^3}}}{3} + x} \right]_1^3\)
\({S_2} = \left( {\frac{1}{6} \cdot \frac{{27}}{3} + 3} \right) - \left( {\frac{1}{6} \cdot \frac{1}{3} + 1} \right)\)
\({S_2} = \left( {\frac{9}{6} + 3} \right) - \left( {\frac{1}{{18}} + 1} \right)\)
\({S_2} = (1.5 + 3) - \left( {\frac{1}{{18}} + 1} \right) = 4.5 - \frac{{19}}{{18}} = \frac{{81}}{{18}} - \frac{{19}}{{18}} = \frac{{62}}{{18}} \approx 3,44\)
c) Tính diện tích hình phẳng giữa hai đồ thị
Diện tích hình phẳng giới hạn bởi hai đồ thị \(f(x)\) và \(g(x)\) trong khoảng \(x = 1\) đến \(x = 3\) là:
\(S = {S_1} - {S_2} = 8 - 3,44 = 4,56\)
Vậy, diện tích hình phẳng giữa hai đồ thị là \(S = 4,56\).
Trả lời câu hỏi Luyện tập 2 trang 26 SGK Toán 12 Cùng khám phá
Tính diện tích hình phẳng được tô màu trong Hình 4.18.
Phương pháp giải:
- Xác định giao điểm của hai đường \(y = {x^3}\) và \(y = x\) bằng cách giải phương trình: \({x^3} = x\)
- Diện tích hình phẳng giữa hai đường cong \(y = {x^3}\) và \(y = x\) trong khoảng từ \(x = - 1\) đến \(x = 1\) được tính bằng:
\(S = \int_{ - 1}^1 | x - {x^3}|{\mkern 1mu} dx\)
Lời giải chi tiết:
Giao điểm của hai đường \(y = {x^3}\) và \(y = x\) là:
\({x^3} = x \Leftrightarrow x({x^2} - 1) = 0\)
Suy ra: \(x = 0\), \(x = 1\), và \(x = - 1\).
Vì trên khoảng từ \( - 1\) đến 0, \(y = {x^3}\) nằm trên \(y = x\), và trên khoảng từ 0 đến 1, \(y = x\) nằm trên \(y = {x^3}\), ta có:
\(S = \int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx + \int_0^1 {(x - {x^3})} {\mkern 1mu} dx\)
Tính tích phân:
\(\int_{ - 1}^0 {({x^3} - x)} {\mkern 1mu} dx = \left[ {\frac{{{x^4}}}{4} - \frac{{{x^2}}}{2}} \right]_{ - 1}^0 = \left( {0 - 0} \right) - \left( {\frac{1}{4} - \frac{1}{2}} \right) = - \frac{1}{4} + \frac{1}{2} = \frac{1}{4}\)
\(\int_0^1 {(x - {x^3})} {\mkern 1mu} dx = \left[ {\frac{{{x^2}}}{2} - \frac{{{x^4}}}{4}} \right]_0^1 = \left( {\frac{1}{2} - \frac{1}{4}} \right) - (0 - 0) = \frac{1}{4}\)
Vậy diện tích hình phẳng là:
\(S = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).
Giải mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2 - Cùng khám phá
Mục 1 của SGK Toán 12 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng đạo hàm để khảo sát hàm số và giải các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất. Việc nắm vững kiến thức trong mục này là vô cùng quan trọng, vì nó là nền tảng cho các kiến thức nâng cao hơn trong chương trình Toán 12.
Nội dung chính của Mục 1 SGK Toán 12 tập 2
- Đạo hàm của hàm số: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm. Các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến của hàm số. Tìm cực trị của hàm số. Vẽ đồ thị hàm số.
- Bài toán giá trị lớn nhất, giá trị nhỏ nhất: Giải các bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hoặc tập hợp cho trước.
Giải chi tiết các bài tập trang 22, 23, 24, 25, 26
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 22, 23, 24, 25, 26 SGK Toán 12 tập 2:
Bài 1 (Trang 22)
Đề bài: Tính đạo hàm của các hàm số sau:
- y = x3 - 2x2 + 5x - 1
- y = (x2 + 1)(x - 3)
Lời giải:
a) y' = 3x2 - 4x + 5
b) y' = (2x)(x - 3) + (x2 + 1)(1) = 2x2 - 6x + x2 + 1 = 3x2 - 6x + 1
Bài 2 (Trang 23)
Đề bài: Tìm đạo hàm của hàm số y = sin(2x + 1)
Lời giải: y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Bài 3 (Trang 24)
Đề bài: Xác định khoảng đồng biến, nghịch biến của hàm số y = x2 - 4x + 3
Lời giải:
y' = 2x - 4
y' > 0 khi 2x - 4 > 0 => x > 2. Vậy hàm số đồng biến trên khoảng (2, +∞)
y' < 0 khi 2x - 4 < 0 => x < 2. Vậy hàm số nghịch biến trên khoảng (-∞, 2)
Bài 4 (Trang 25)
Đề bài: Tìm cực trị của hàm số y = x3 - 3x2 + 2
Lời giải:
y' = 3x2 - 6x
y' = 0 khi 3x2 - 6x = 0 => x = 0 hoặc x = 2
y'' = 6x - 6
y''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0, ymax = 2
y''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, ymin = -2
Bài 5 (Trang 26)
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x2 - 2x + 1 trên đoạn [-1, 3]
Lời giải:
y' = 2x - 2
y' = 0 khi x = 1
Tính giá trị của hàm số tại các điểm x = -1, x = 1, x = 3:
y(-1) = 4
y(1) = 0
y(3) = 4
Vậy giá trị lớn nhất của hàm số trên đoạn [-1, 3] là 4, đạt được tại x = -1 và x = 3. Giá trị nhỏ nhất của hàm số trên đoạn [-1, 3] là 0, đạt được tại x = 1.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về các bài tập trong mục 1 SGK Toán 12 tập 2. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. Chúc các em học tốt!