Giải mục 2 trang 52, 53, 54 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 52, 53, 54 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 52, 53, 54 SGK Toán 12 tập 1 trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng: - Độ dài của vectơ. - Giá của vectơ. - Hai vectơ cùng phương, hai vectơ cùng hướng. - Hai vectơ bằng nhau. - Hai vectơ đối nhau. - Vectơ-không.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 52 SGK Toán 12 Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.
Phương pháp giải:
Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.
Lời giải chi tiết:
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
- HĐ2
- LT2
Trả lời câu hỏi Hoạt động 2 trang 52 SGK Toán 12 Cùng khám phá
Nhắc lại các khái niệm liên quan đến vectơ trong mặt phẳng:
- Độ dài của vectơ.
- Giá của vectơ.
- Hai vectơ cùng phương, hai vectơ cùng hướng.
- Hai vectơ bằng nhau.
- Hai vectơ đối nhau.
- Vectơ-không.
Phương pháp giải:
Các khái niệm liên quan đến vectơ trong không gian có trong Sách giáo khoa trang 52.
Lời giải chi tiết:
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Độ dài của vectơ \(\vec a\) được kí hiệu là \(|\vec a|\).
- Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
- Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng. Vectơ đối của \(\vec a\) được kí hiệu là \( - \vec a\).
- Vectơ-không có độ dài bằng 0 và cùng phương, cùng hướng với mọi vectơ.
Trả lời câu hỏi Luyện tập 2 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).
Phương pháp giải:
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết:
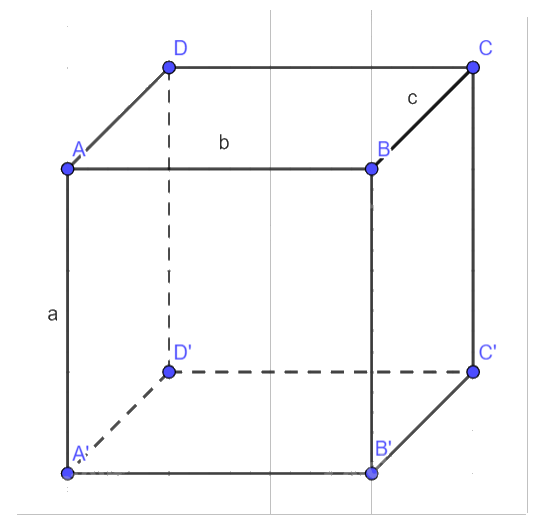
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA'C'\) vuông tại \(A'\). Từ đó ta có:
\(\begin{array}{l}AC' = \sqrt {{{(AA')}^2} + {{(A'C')}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC' = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)
LT2
Trả lời câu hỏi Luyện tập 2 trang 54 SGK Toán 12 Cùng khám phá
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\).
a) Trong các vectơ khác \(\vec 0\), có điểm đầu và̀ điểm cuối là các đỉnh của hình hộp, hãy chỉ ra những vectơ:
- Cùng phương với vectơ \(\overrightarrow {AB} \);
- Bä̀ng vectơ \(\overrightarrow {AB} \);
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \).
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \) trong trường hợp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, có \(A{A^\prime } = \) a, \(AB = b,BC = c\) và \(\widehat {ABC} = {120^o}\).
Phương pháp giải:
a) Xác định các vectơ theo yêu cầu đề bài dựa trên lý thuyết về vectơ.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
- Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng. Nếu hai vectơ \(\vec a,\vec b\) bằng nhau thì ta viết là \(\vec a = \vec b\).
b) Sử dụng công thức và định lý để tính độ dài của vectơ.
Lời giải chi tiết:
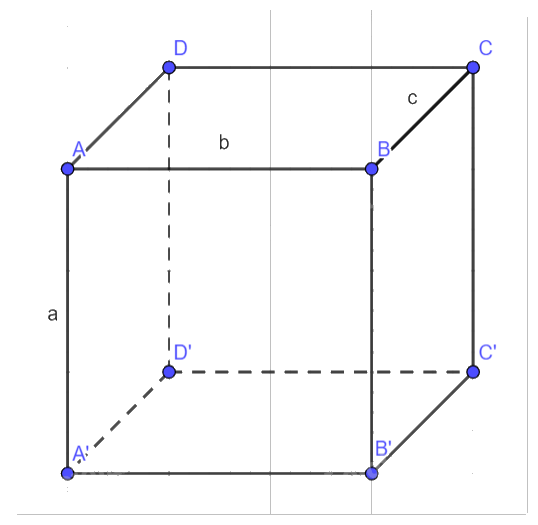
a) Các vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp:
- Cùng phương với vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {{A^\prime }{B^\prime }} \), \(\overrightarrow {DC} \), \(\overrightarrow {{D^\prime }{C^\prime }} \),\(\overrightarrow {{B^\prime }{A^\prime }} \), \(\overrightarrow {CD} \), \(\overrightarrow {{C^\prime }{D^\prime }} \),\(\overrightarrow {BA} \)
- Bằng vectơ \(\overrightarrow {AB} \) :\(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} = \overrightarrow {DC} = \overrightarrow {{D^\prime }{C^\prime }} \)
- Ngược hướng với vectơ \(\overrightarrow {A{A^\prime }} \): \(\overrightarrow {{B^\prime }B} \),\(\overrightarrow {{C^\prime }C} \),\(\overrightarrow {{D^\prime }D} \),\(\overrightarrow {{A^\prime }A} \)
b) Tính độ dài của vectơ \(\overrightarrow {A{C^\prime }} \):
- Vì \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình hộp đứng, suy ra tam giác \(AA'C'\) vuông tại \(A'\). Từ đó ta có:
\(\begin{array}{l}AC' = \sqrt {{{(AA')}^2} + {{(A'C')}^2}} = \sqrt {{a^2} + A{C^2}} = \sqrt {{a^2} + (A{B^2} + B{C^2} - 2.AB.BC.\cos (120^\circ )} \\AC' = \sqrt {{a^2} + {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right)} = \sqrt {{a^2} + {b^2} + {c^2} - bc} \end{array}\)
Vậy độ dài của vectơ \(\overrightarrow {A{C^\prime }} \)là: \(\sqrt {{a^2} + {b^2} + {c^2} - bc} \)
Giải mục 2 trang 52, 53, 54 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo và các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chi tiết Giải mục 2 trang 52, 53, 54
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2, chúng ta sẽ đi vào phân tích chi tiết từng bài tập trên trang 52, 53 và 54.
Bài 1: Trang 52 - Tính đạo hàm của hàm số
Bài tập này yêu cầu các em vận dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số cho trước. Lưu ý khi giải bài tập này là cần nắm vững các công thức đạo hàm cơ bản và quy tắc chuỗi, quy tắc tích, quy tắc thương.
Ví dụ:
- Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1
- Tính đạo hàm của hàm số y = (x2 + 1)(x - 2)
Bài 2: Trang 53 - Tìm đạo hàm cấp hai
Bài tập này yêu cầu các em tìm đạo hàm cấp hai của hàm số, tức là đạo hàm của đạo hàm cấp nhất. Để giải bài tập này, các em cần thực hiện tuần tự các bước: tìm đạo hàm cấp nhất, sau đó tìm đạo hàm của đạo hàm cấp nhất để được đạo hàm cấp hai.
Bài 3: Trang 54 - Ứng dụng đạo hàm để tìm cực trị
Bài tập này yêu cầu các em sử dụng đạo hàm để tìm cực trị của hàm số. Để giải bài tập này, các em cần thực hiện các bước sau:
- Tìm tập xác định của hàm số.
- Tính đạo hàm cấp nhất của hàm số.
- Tìm các điểm dừng (điểm mà đạo hàm cấp nhất bằng 0 hoặc không xác định).
- Khảo sát dấu của đạo hàm cấp nhất để xác định các điểm cực trị (cực đại, cực tiểu).
- Tính giá trị của hàm số tại các điểm cực trị.
Lưu ý quan trọng khi giải bài tập
Khi giải các bài tập về đạo hàm, các em cần lưu ý những điều sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Vận dụng linh hoạt các quy tắc tính đạo hàm.
- Kiểm tra lại kết quả sau khi giải xong.
- Thực hành thường xuyên để nâng cao kỹ năng giải bài tập.
Tusach.vn – Đồng hành cùng các em trên con đường học tập
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập. Ngoài lời giải chi tiết các bài tập trong SGK, chúng tôi còn cung cấp nhiều tài liệu học tập hữu ích khác, như bài giảng, đề thi thử, và các bài viết chuyên sâu về các chủ đề Toán học. Hãy truy cập tusach.vn để khám phá thêm nhiều điều thú vị và hữu ích nhé!
Bảng tổng hợp các công thức đạo hàm cơ bản
| Hàm số | Đạo hàm |
|---|---|
| y = c (c là hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |