Giải bài tập 1.32 trang 45 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.32 Trang 45 SGK Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.32 trang 45 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và đầy đủ nhất.
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu?
Đề bài
Trong một cuộc thi làm đồ dùng học tập do trường phát động, bạn Nam làm một hình chóp tứ giác đều S.EFGH bằng cách sử dụng một tấm bìa hình vuông ABCD có cạnh bằng 5 cm và cắt tấm bìa theo các tam giác cân AEB, BFC, CGD, DHA. Sau đó bạn gấp các tam giác AEH, BEF, CFG, DGH sao cho bốn đỉnh A, B, C, D trùng nhau tạo thành đỉnh S của khối chóp tứ giác đều như hình 1.66. Thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng bao nhiêu?
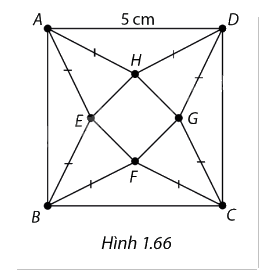
Phương pháp giải - Xem chi tiết
- Đặt x là độ dài các cạnh của hình vuông EFGH.
- Tính diện tích của hình vuông EFGH theo x.
- Tìm chiều cao từ đỉnh S xuống đáy.
- Tìm hàm thể tích và khảo sát.
Lời giải chi tiết
Theo đề bài ta có hình vẽ như sau:
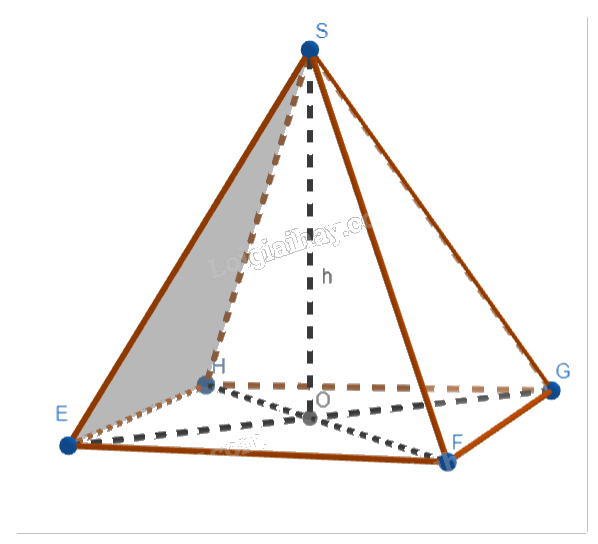
- Đặt x (cm) là độ dài các cạnh của hình vuông EFGH (x∈\((0;2,5\sqrt 2 )\)).
Tương đương EF=FG=GH=EH=x nên \({S_{EFGH}} = {x^2}\)
Đặt SO là chiều cao của hình chóp S.EFGH.
- Độ dài đường chéo của hình vuông EFGH là \(HF = EG = \sqrt {{x^2} + {x^2}} = x\sqrt 2 \)cm.
- Ta có: \(SE = AE = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{5 - x\sqrt 2 }}{2}} \right)}^2}} = \sqrt {2.{{\left( {\frac{5}{2}} \right)}^2} - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 2{x^2}} \)
- Vì tam giác vuông SOE vuông tại O nên suy ra:
\(SO = \sqrt {S{E^2} - E{O^2}} = \sqrt {\frac{1}{4}(50 - 2{x^2}) - \frac{{2{x^2}}}{4}} = \frac{1}{2}\sqrt {50 - 4{x^2}} \)
- Thể tích của hình chóp S.EFGH là:
\({V_{S.EFGH}} = \frac{1}{3}.{S_{EFGH}}.SO = \frac{1}{3}.{x^2}.\frac{1}{2}\sqrt {50 - 4{x^2}} = \frac{1}{6}{x^2}\sqrt {50 - 4{x^2}} \)
Để thể tích hình chóp S.EFGH là lớn nhất thì \(f(x) = {x^2}\sqrt {50 - 4{x^2}} \) phải đạt giá trị lớn nhất trong khoảng từ \((0;2,5\sqrt 2 )\).
- Tính đạo hàm: \(f'(x) = 2x\sqrt {50 - 4{x^2}} + {x^2}.\frac{{ - 4x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{ - 12{x^3} + 100x}}{{\sqrt {50 - 4{x^2}} }} = \frac{{4x(3{x^2} - 25)}}{{\sqrt {50 - 4{x^2}} }}\)
- Giải phương trình \(f'(x) = 0\)
\[4x(3{x^2} - 25) = 0 \Leftrightarrow {x_1} = 0,{x_2} = \frac{5}{{\sqrt 3 }},{x_3} = - \frac{5}{{\sqrt 3 }}\](loại \({x_1},{x_3}\) vì x > 0).
- Bảng biến thiên:
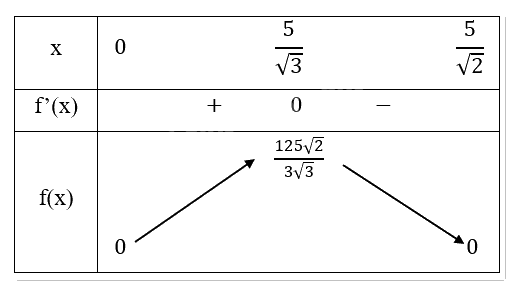
Nhận thấy \(f(x)\) sẽ đạt giá trị lớn nhất tại \(x = \frac{5}{{\sqrt 3 }}\)
Vậy thể tích lớn nhất của khối chóp tứ giác đều tạo thành là \(V = \frac{1}{6}.{\left( {\frac{5}{{\sqrt 3 }}} \right)^2}.\sqrt {50 - 4{{\left( {\frac{5}{{\sqrt 3 }}} \right)}^2}} \approx 5,67c{m^3}\).
Giải Bài Tập 1.32 Trang 45 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu
Bài tập 1.32 trang 45 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.
Đề Bài Bài Tập 1.32 Trang 45 SGK Toán 12 Tập 1
(Đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = x3 - 3x2 + 2. Khảo sát hàm số và tìm các điểm cực trị.)
Phương Pháp Giải Bài Tập Khảo Sát Hàm Số
- Xác định tập xác định của hàm số: Kiểm tra xem có giá trị nào của x làm mẫu số bằng 0 hoặc biểu thức trong căn bậc hai âm không.
- Tính đạo hàm cấp một (y'): Sử dụng các quy tắc đạo hàm để tìm y'.
- Tìm điểm dừng (x0): Giải phương trình y' = 0 để tìm các giá trị x0.
- Lập bảng biến thiên: Xác định dấu của y' trên các khoảng xác định bởi các điểm dừng. Từ đó suy ra hàm số đồng biến, nghịch biến trên các khoảng đó.
- Tìm cực trị: Sử dụng dấu của y' để xác định các điểm cực đại, cực tiểu.
- Tìm giới hạn vô cùng: Tính limx→+∞ y và limx→-∞ y để xác định tiệm cận ngang (nếu có).
- Vẽ đồ thị hàm số: Dựa vào các thông tin đã thu thập để vẽ đồ thị hàm số.
Lời Giải Chi Tiết Bài Tập 1.32 Trang 45 SGK Toán 12 Tập 1
(Lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước tính toán, giải thích rõ ràng và kết luận.)
Ví dụ, nếu đề bài là y = x3 - 3x2 + 2:
- Tập xác định: D = R
- y' = 3x2 - 6x
- y' = 0 ⇔ 3x2 - 6x = 0 ⇔ x = 0 hoặc x = 2
- Bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Hàm số đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2). Điểm cực đại là (0; 2), điểm cực tiểu là (2; -2).
Lưu Ý Khi Giải Bài Tập Khảo Sát Hàm Số
- Luôn kiểm tra kỹ tập xác định của hàm số.
- Tính đạo hàm chính xác và cẩn thận.
- Lập bảng biến thiên một cách khoa học và rõ ràng.
- Kết hợp các kiến thức về giới hạn vô cùng để xác định tiệm cận.
Tusach.vn – Đồng Hành Cùng Bạn Học Toán 12
Tusach.vn hy vọng với lời giải chi tiết và phương pháp giải bài tập khảo sát hàm số trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập 1.32 trang 45 SGK Toán 12 tập 1 và tự tin hơn trong quá trình học tập. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!