Giải mục 2 trang 43, 44, 45, 46 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 43, 44, 45, 46 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 43, 44, 45, 46 SGK Toán 12 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục 2 này thường xoay quanh các kiến thức về tích phân, ứng dụng của tích phân trong tính diện tích, hoặc các bài toán liên quan đến đạo hàm.
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\). Gọi \(M(x;y;z)\) là một điểm tùy ý (Hình 5.5). Hãy điền các kí tự thích hợp vào \(?\). Điều kiện cần và đủ để điểm \(M(x;y;z)\) thuộc \((\alpha )\) là: \(\vec n \cdot \overrightarrow {{M_0}M} = ?\) Hay: \(A(x - ?) + B(y - ?) + C(z - ?) = 0\) (*) Đặt \(D = - (A{x_0} + B{y_0} + C{z_0})\) thì phương trình (*) trở thành: \(?x + ?y + ?z + D = 0\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tìm một vectơ pháp tuyến của các mặt phẳng sau:
a) \((\alpha ):x - 5y + 2 = 0;\)
b) \((\beta ):2y + 3 = 0.\)
Phương pháp giải:
Phương trình tổng quát của mặt phẳng trong không gian Oxyz có dạng:
\(Ax + By + Cz + D = 0\)
Vectơ pháp tuyến của mặt phẳng này là \(\vec n = (A,B,C)\), trong đó \(A\), \(B\), \(C\) là các hệ số của \(x\), \(y\), \(z\) trong phương trình.
Lời giải chi tiết:
a) Mặt phẳng \((\alpha ):x - 5y + 2 = 0\).
So sánh với phương trình tổng quát \(Ax + By + Cz + D = 0\), ta có:
\(A = 1,\quad B = - 5,\quad C = 0\)
Do đó, vectơ pháp tuyến của mặt phẳng \((\alpha )\) là:
\(\overrightarrow {{n_\alpha }} = (1, - 5,0)\)
b) Mặt phẳng \((\beta ):2y + 3 = 0\).
So sánh với phương trình tổng quát \(Ax + By + Cz + D = 0\), ta có:
\(A = 0,\quad B = 2,\quad C = 0\)
Do đó, vectơ pháp tuyến của mặt phẳng \((\beta )\) là:
\(\overrightarrow {{n_\beta }} = (0,2,0)\)
LT4
Trả lời câu hỏi Luyện tập 4 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(M(1;1;1)\), \(N(4;3;2)\), \(P(5;2;1)\). Viết phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P\) và vuông góc với \(MN\).
Phương pháp giải:
- Tìm vectơ chỉ phương của đường thẳng \(MN\) bằng cách lấy hiệu tọa độ của \(N\) và \(M\):
\(\overrightarrow {MN} = N - M\)
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là chính vectơ chỉ phương của đường thẳng \(MN\), vì mặt phẳng vuông góc với đường thẳng này.
- Phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\) có dạng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
Tính vectơ chỉ phương của \(MN\):
\(\overrightarrow {MN} = N - M = (4 - 1,3 - 1,2 - 1) = (3,2,1)\)
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n = (3,2,1)\).
Phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P(5;2;1)\) có dạng:
\(3(x - 5) + 2(y - 2) + 1(z - 1) = 0\)
Khai triển biểu thức trên:
\(3x - 15 + 2y - 4 + z - 1 = 0\)
\(3x + 2y + z - 20 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((\alpha )\) là:
\(3x + 2y + z - 20 = 0\)
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt phẳng \((P)\) đi qua điểm \(M(2; - 1;3)\) và có cặp vectơ chỉ phương \(\vec a = (2;1; - 2)\), \(\vec b = (2; - 1;0)\).
a) Tìm \([\vec a,\vec b]\), và một vectơ pháp tuyến của \((P)\)
b) Viết phương trình tổng quát của mặt phẳng \((P)\).
Phương pháp giải:
- Tính tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) để tìm vectơ pháp tuyến của mặt phẳng \((P)\). Công thức tính tích có hướng:
\(\vec n = \vec a \times \vec b = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\)
- Sử dụng phương trình tổng quát của mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
Tính tích có hướng \(\vec n = \vec a \times \vec b\):
\(\vec n = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\2&1&{ - 2}\\2&{ - 1}&0\end{array}} \right|\)
Tính từng bước:
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&0\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}2&{ - 2}\\2&0\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}2&1\\2&{ - 1}\end{array}} \right|\)
\( = {\bf{i}}(1 \cdot 0 - ( - 2) \cdot ( - 1)) - {\bf{j}}(2 \cdot 0 - ( - 2) \cdot 2) + {\bf{k}}(2 \cdot ( - 1) - 1 \cdot 2)\)
\( = {\bf{i}}(0 - 2) - {\bf{j}}(0 + 4) + {\bf{k}}( - 2 - 2)\)
\( = ( - 2, - 4, - 4)\)
Vậy vectơ pháp tuyến của mặt phẳng \((P)\) là:
\(\vec n = ( - 2, - 4, - 4)\)
Viết phương trình tổng quát của mặt phẳng \((P)\) đi qua điểm \(M(2; - 1;3)\):
\( - 2(x - 2) - 4(y + 1) - 4(z - 3) = 0\)
Khai triển:
\( - 2x + 4 - 4y - 4 - 4z + 12 = 0\)
\( - 2x - 4y - 4z + 12 = 0\)
Chia cả hai vế cho \( - 2\):
\(x + 2y + 2z - 6 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((P)\) là:
\(x + 2y + 2z - 6 = 0\)
LT5
Trả lời câu hỏi Luyện tập 5 trang 45 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba vectơ \(\vec a = (1; - 2;3)\), \(\vec b = (3;2; - 1)\), \(\vec c = ( - 2;4; - 6)\) và điểm \(A(4;1;0)\). Viết phương trình tổng quát của các mặt phẳng đi qua \(A\) và nhận hai trong ba vectơ \(\vec a,\vec b,\vec c\) làm cặp vectơ chỉ phương.
Phương pháp giải:
1. Chọn hai vectơ chỉ phương từ ba vectơ \(\vec a,\vec b,\vec c\).
2. Tìm tích có hướng của hai vectơ đã chọn để tìm vectơ pháp tuyến của mặt phẳng.
3. Viết phương trình tổng quát của mặt phẳng đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\):
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
- Mặt phẳng thứ nhất chứa \(\vec a\) và \(\vec b\):
Tích có hướng của \(\vec a\) và \(\vec b\):
\({\vec n_1} = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 2}&3\\2&{ - 1}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}1&3\\3&{ - 1}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\3&2\end{array}} \right|\)
\( = {\bf{i}}(\left( { - 2} \right) \cdot ( - 1) - 3 \cdot 2) - {\bf{j}}(1 \cdot ( - 1) - 3 \cdot 3) + {\bf{k}}(1 \cdot 2 - ( - 2) \cdot 3)\)
\( = {\bf{i}}( - 2 - 6) - {\bf{j}}( - 1 - 9) + {\bf{k}}(2 + 6)\)
\( = ( - 4,10,8)\)
Vậy vectơ pháp tuyến của mặt phẳng 1 là \({\vec n_1} = ( - 4,10,8)\). 2. Viết phương trình tổng quát của mặt phẳng 1 đi qua điểm \(A(4;1;0)\):
\( - 4(x - 4) + 10(y - 1) + 8(z - 0) = 0\)
\( - 4x + 16 + 10y - 10 + 8z = 0\)
\( - 4x + 10y + 8z + 6 = 0\)
Vậy phương trình tổng quát của mặt phẳng thứ nhất là:
\( - 4x + 10y + 8z + 6 = 0\)
- Mặt phẳng thứ hai chứa \(\vec a\) và \(\vec c\):
Tích có hướng của \(\vec a\) và \(\vec c\):
\({\vec n_2} = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 2}&3\\4&{ - 6}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}1&3\\{ - 2}&{ - 6}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 2}&4\end{array}} \right|\)
\( = {\bf{i}}(( - 2) \cdot ( - 6) - 3 \cdot 4) - {\bf{j}}(1 \cdot ( - 6) - 3 \cdot ( - 2)) + {\bf{k}}(1 \cdot 4 - ( - 2) \cdot ( - 2))\)
\( = {\bf{i}}(12 - 12) - {\bf{j}}( - 6 + 6) + {\bf{k}}(4 - 4)\)
\( = (0,0,0)\)
Kết quả cho thấy hai vectơ \(\vec a\) và \(\vec c\) cùng phương, nên không tạo thành mặt phẳng mới. Chúng ta không cần xét tiếp trường hợp này.
- Mặt phẳng thứ 3 chứa \(\vec b\) và \(\vec c\):
Tích có hướng của \(\vec b\) và \(\vec c\):
\({\vec n_3} = {\bf{i}}\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 6}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}3&{ - 1}\\{ - 2}&{ - 6}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}3&2\\{ - 2}&4\end{array}} \right|\)
\( = {\bf{i}}(2 \cdot ( - 6) - ( - 1) \cdot 4) - {\bf{j}}(3 \cdot ( - 6) - ( - 1) \cdot ( - 2)) + {\bf{k}}(3 \cdot 4 - 2 \cdot ( - 2))\)
\( = {\bf{i}}( - 12 + 4) - {\bf{j}}( - 18 - 2) + {\bf{k}}(12 + 4)\)
\( = ( - 8, - 20,16)\)
Vậy vectơ pháp tuyến của mặt phẳng 3 là \({\vec n_3} = ( - 8, - 20,16)\). 2. Viết phương trình tổng quát của mặt phẳng 3 đi qua điểm \(A(4;1;0)\):
\( - 8(x - 4) - 20(y - 1) + 16(z - 0) = 0\)
\( - 8x + 32 - 20y + 20 + 16z = 0\)
\( - 8x - 20y + 16z + 52 = 0\)
Vậy phương trình tổng quát của mặt phẳng thứ 3 là:
\( - 8x - 20y + 16z + 52 = 0\)
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 45 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(A(4; - 1;2)\), \(B(1;4; - 3)\), \(C(3; - 4;7)\).
a) Chứng minh ba điểm \(A\), \(B\), \(C\) không thẳng hàng.
b) Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \((ABC)\).
c) Viết phương trình tổng quát của mặt phẳng \((ABC)\).
Phương pháp giải:
1. Để chứng minh ba điểm \(A\), \(B\), \(C\) không thẳng hàng, tính hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Nếu hai vectơ này không cùng phương thì ba điểm không thẳng hàng.
2. Tìm tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) để tìm vectơ pháp tuyến của mặt phẳng.
3. Sử dụng phương trình tổng quát của mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
a) Tính các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = B - A = (1 - 4,4 + 1, - 3 - 2) = ( - 3,5, - 5)\)
\(\overrightarrow {AC} = C - A = (3 - 4, - 4 + 1,7 - 2) = ( - 1, - 3,5)\)
Xét tỉ số giữa các tọa độ của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\frac{{ - 3}}{{ - 1}} = 3,\quad \frac{5}{{ - 3}} = - \frac{5}{3},\quad \frac{{ - 5}}{5} = - 1\)
Các tỉ số không bằng nhau, nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương. Do đó, ba điểm \(A\), \(B\), \(C\) không thẳng hàng.
b) Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}5&{ - 5}\\{ - 3}&5\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}{ - 3}&{ - 5}\\{ - 1}&5\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}{ - 3}&5\\{ - 1}&{ - 3}\end{array}} \right|\)
\( = {\bf{i}}(5 \cdot 5 - ( - 5) \cdot ( - 3)) - {\bf{j}}(( - 3) \cdot 5 - ( - 5) \cdot ( - 1)) + {\bf{k}}(( - 3) \cdot ( - 3) - 5 \cdot ( - 1))\)
\( = {\bf{i}}(25 - 15) - {\bf{j}}(( - 15 - 5)) + {\bf{k}}(9 + 5)\)
\( = (10,20,14)\)
Vậy vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\vec n = (10,20,14)\).
c) Viết phương trình tổng quát của mặt phẳng đi qua điểm \(A(4; - 1;2)\):
\(10(x - 4) + 20(y + 1) + 14(z - 2) = 0\)
\(10x - 40 + 20y + 20 + 14z - 28 = 0\)
\(10x + 20y + 14z - 48 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((ABC)\) là:
\(10x + 20y + 14z - 48 = 0\)
LT6
Trả lời câu hỏi Luyện tập 6 trang 46 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho bốn điểm \(A(4;0;0)\), \(B(0; - 5;0)\), \(C(0;0;6)\), \(D( - 5;3;4)\). Viết phương trình các mặt phẳng \((ABC)\), \((BCD)\), \((ABD)\), \((ACD)\).
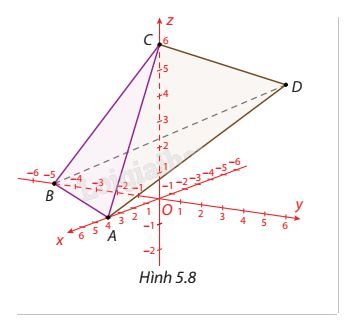
Phương pháp giải:
1. Xác định các vectơ chỉ phương từ các điểm đã cho. Ví dụ, để viết phương trình mặt phẳng \((ABC)\), ta tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
2. Tìm vectơ pháp tuyến của mặt phẳng bằng cách lấy tích có hướng của hai vectơ chỉ phương vừa tìm được.
3. Sử dụng phương trình tổng quát của mặt phẳng:
\(Ax + By + Cz + D = 0\)
với \((A,B,C)\) là tọa độ của vectơ pháp tuyến và \(D = - (A{x_0} + B{y_0} + C{z_0})\), trong đó \(({x_0},{y_0},{z_0})\) là tọa độ của một điểm thuộc mặt phẳng.
Lời giải chi tiết:
1. Phương trình mặt phẳng \((ABC)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = B - A = (0 - 4, - 5 - 0,0 - 0) = ( - 4, - 5,0)\)
\(\overrightarrow {AC} = C - A = (0 - 4,0 - 0,6 - 0) = ( - 4,0,6)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\left( {( - 5).6 - 0.0,0.( - 4) - ( - 4).6,( - 4).0 - ( - 5).( - 4)} \right)\)
\( = ( - 30,24, - 20)\)
Phương trình mặt phẳng \((ABC)\) là:
\( - 30(x - 4) + 24(y - 0) - 20(z - 0) = 0\)
\( - 30x + 120 + 24y - 20z = 0\)
\(30x - 24y + 20z = 120\)
Vậy phương trình mặt phẳng \((ABC)\) là:
\(30x - 24y + 20z = 120\)
2. Phương trình mặt phẳng \((BCD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \):
\(\overrightarrow {BC} = C - B = (0 - 0,0 - ( - 5),6 - 0) = (0,5,6)\)
\(\overrightarrow {BD} = D - B = ( - 5 - 0,3 - ( - 5),4 - 0) = ( - 5,8,4)\)
Tích có hướng của \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \):
\(\left( {5.4 - 6.8,6.( - 5) - 0.4,0.8 - ( - 5).5} \right)\)
\( = ( - 28, - 30,25)\)
Phương trình mặt phẳng \((BCD)\) là:
\( - 28(x - 0) - 30(y + 5) + 25(z - 0) = 0\)
\( - 28x - 30y - 150 + 25z = 0\)
\(28x + 30y - 25z = - 150\)
Vậy phương trình mặt phẳng \((BCD)\) là:
\(28x + 30y - 25z = - 150\)
3. Phương trình mặt phẳng \((ABD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AB} = ( - 4, - 5,0)\)
\(\overrightarrow {AD} = D - A = ( - 5 - 4,3 - 0,4 - 0) = ( - 9,3,4)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\left( {( - 5).4 - 0.3,\,\,0.( - 9) - ( - 4).4,\,\,( - 4).3 - ( - 5).( - 9)} \right)\)
\( = ( - 20,16, - 57)\)
Phương trình mặt phẳng \((ABD)\) là:
\( - 20(x - 4) + 16(y - 0) - 57(z - 0) = 0\)
\( - 20x + 80 + 16y - 57z = 0\)
\(20x - 16y + 57z = 80\)
Vậy phương trình mặt phẳng \((ABD)\) là:
\(20x - 16y + 57z = 80\)
4. Phương trình mặt phẳng \((ACD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AC} = ( - 4,0,6)\)
\(\overrightarrow {AD} = ( - 9,3,4)\)
Tích có hướng của \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \):
\(\left( {0.4 - 6.3,\,\,6.( - 9) - ( - 4).4,\,\,( - 4).3 - 0.( - 9)} \right)\)
\(( - 18, - 38, - 12)\)
Phương trình mặt phẳng \((ACD)\) là:
\( - 18(x - 4) - 38(y - 0) - 12(z - 0) = 0\)
\( - 18x + 72 - 38y - 12z = 0\)
\(18x + 38y + 12z = 72\)
Vậy phương trình mặt phẳng \((ACD)\) là:
\(18x + 38y + 12z = 72\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 43 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\). Gọi \(M(x;y;z)\) là một điểm tùy ý (Hình 5.5). Hãy điền các kí tự thích hợp vào \(?\). Điều kiện cần và đủ để điểm \(M(x;y;z)\) thuộc \((\alpha )\) là:
\(\vec n \cdot \overrightarrow {{M_0}M} = ?\)
Hay:
\(A(x - ?) + B(y - ?) + C(z - ?) = 0\) (*)
Đặt \(D = - (A{x_0} + B{y_0} + C{z_0})\) thì phương trình (*) trở thành:
\(?x + ?y + ?z + D = 0\)
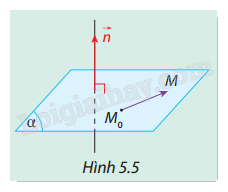
Phương pháp giải:
Để xác định phương trình mặt phẳng, ta cần biết một điểm thuộc mặt phẳng \(({x_0},{y_0},{z_0})\) và một vectơ pháp tuyến \((A,B,C)\). Sử dụng công thức tổng quát của phương trình mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc:
\(Ax + By + Cz + D = 0\)
Một điểm \(M(x;y;z)\) nằm trên mặt phẳng khi và chỉ khi thay tọa độ của điểm đó vào phương trình mặt phẳng, vế trái bằng 0.
Lời giải chi tiết:
Phương trình tổng quát của mặt phẳng \((\alpha )\):
Giả sử mặt phẳng \((\alpha )\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\). Phương trình mặt phẳng là:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc dưới dạng khác:
\(Ax + By + Cz + D = 0\)
với:
\(D = - (A{x_0} + B{y_0} + C{z_0})\)
Ý nghĩa điều kiện \(\vec n \cdot \overrightarrow {{M_0}M} = 0\):
Điều kiện này biểu diễn rằng tích vô hướng giữa vectơ pháp tuyến \(\vec n\) và vectơ \(\overrightarrow {{M_0}M} \) (nối từ \({M_0}\) đến một điểm bất kỳ \(M\)) bằng 0, có nghĩa là hai vectơ này vuông góc, đảm bảo rằng điểm \(M\) nằm trên mặt phẳng.
VD1
Trả lời câu hỏi Vận dụng 1 trang 46 SGK Toán 12 Cùng khám phá
Một phần sân nhà bác An có dạng hình thang \(ABCD\) vuông tại \(A\) và \(B\) với độ dài \(AB = 9{\mkern 1mu} m\), \(AD = 5{\mkern 1mu} m\) và \(BC = 6{\mkern 1mu} m\) như Hình 5.9. Theo thiết kế ban đầu thì mặt sân bằng phẳng và các điểm \(A\), \(B\), \(C\), \(D\) có độ cao như nhau. Sau đó bác An thay đổi thiết kế để nước có thể thoát về phía góc sân ở vị trí \(C\) bằng cách giữ nguyên độ cao ở \(A\), giảm độ cao của sân ở vị trí \(B\) và \(D\) xuống thấp hơn độ cao ở \(A\) lần lượt là \(6{\mkern 1mu} cm\) và \(3,6{\mkern 1mu} cm\). Để mặt sân sau khi lát gạch vẫn là bề mặt phẳng thì bác An cần phải giảm độ cao ở \(C\) xuống bao nhiêu centimet so với độ cao ở \(A\)?
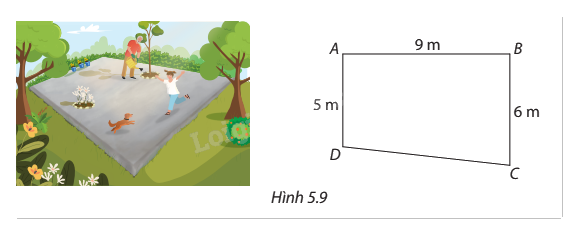
Phương pháp giải:
- Ta coi các độ cao là tọa độ \(z\) của các điểm \(A\), \(B\), \(C\), \(D\) trong không gian. Do độ cao của điểm \(A\) không thay đổi, ta đặt \({z_A} = 0\). Giả sử các tọa độ khác của các điểm là tọa độ trong mặt phẳng \(Oxy\), ta có:
\(A(0;0;0),\quad B(9;0; - 0,06),\quad D(0;5; - 0,036),\quad C({x_C};{y_C};{z_C})\)
- Xác định phương trình mặt phẳng chứa các điểm \(A\), \(B\), \(D\) (vì mặt phẳng này là phẳng nên tọa độ \(z\) của \(C\) phải thỏa mãn phương trình này).
- Tìm tọa độ \({z_C}\) bằng cách giải hệ phương trình.
Lời giải chi tiết:
Gọi độ cao của các điểm \(A,B,C,D\)lần lượt là \({z_A}\), \({z_B}\), \({z_C}\), \({z_D}\). Theo đề bài, ta có:
\({z_A} = {z_B} = {z_D} = 0.\)
Sau khi điều chỉnh, độ cao của các điểm \(B,D\) được thay đổi như sau:
\({z_B} = - 0,06{\mkern 1mu} {\rm{m}},\quad {z_D} = - 0,036{\mkern 1mu} {\rm{m}}.\)
Để mặt sân sau khi lát gạch là một mặt phẳng, ta cần lập phương trình mặt phẳng \((ABCD)\) đi qua ba điểm \(A(0;0;0)\), \(B(9;0; - 0,06)\), \(D(0;5; - 0,036)\). Phương trình mặt phẳng có dạng:
\(Ax + By + Cz + D = 0.\)
Vì mặt phẳng đi qua \(A(0;0;0)\), thay \(A(0;0;0)\) vào phương trình ta được:
\(D = 0.\)
Do đó, phương trình mặt phẳng có dạng:
\(Ax + By + Cz = 0.\)
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AB} = (9;0; - 0,06)\)
\(\overrightarrow {AD} = \left( {0;5; - 0,036} \right)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\left( {0.( - 0,036) - ( - 0,06).5;( - 0,06).0 - 9.( - 0,036);9.5 - 0.0} \right)\)
\( = (0,3;0,324;45)\)
Ta có phương trình mặt phẳng:
\(0,3x + 0,324y + 45z = 0\)
Thay tọa độ \(C(9;6;{z_C})\) vào phương trình:
\(0,3.(9) + 0,324.(6) + 45{z_C} = 0\)
\(2,7 + 1,944 + 45{z_C} = 0\)
\({z_C} = - 0,1032{\mkern 1mu} {\rm{m}}\)
Vậy độ cao của điểm \(C\) cần giảm là:
\({z_C} = - 0.1032{\mkern 1mu} {\rm{m}} = - 10.32{\mkern 1mu} {\rm{cm}}.\)
Bác An cần hạ độ cao của điểm \(C\) xuống khoảng \(10.32{\mkern 1mu} {\rm{cm}}\) so với độ cao của điểm \(A\).
- HĐ3
- LT3
- LT4
- HĐ4
- LT5
- HĐ5
- LT6
- VD1
Trả lời câu hỏi Hoạt động 3 trang 43 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\). Gọi \(M(x;y;z)\) là một điểm tùy ý (Hình 5.5). Hãy điền các kí tự thích hợp vào \(?\). Điều kiện cần và đủ để điểm \(M(x;y;z)\) thuộc \((\alpha )\) là:
\(\vec n \cdot \overrightarrow {{M_0}M} = ?\)
Hay:
\(A(x - ?) + B(y - ?) + C(z - ?) = 0\) (*)
Đặt \(D = - (A{x_0} + B{y_0} + C{z_0})\) thì phương trình (*) trở thành:
\(?x + ?y + ?z + D = 0\)
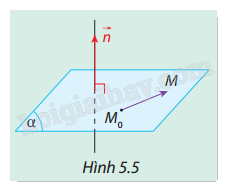
Phương pháp giải:
Để xác định phương trình mặt phẳng, ta cần biết một điểm thuộc mặt phẳng \(({x_0},{y_0},{z_0})\) và một vectơ pháp tuyến \((A,B,C)\). Sử dụng công thức tổng quát của phương trình mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc:
\(Ax + By + Cz + D = 0\)
Một điểm \(M(x;y;z)\) nằm trên mặt phẳng khi và chỉ khi thay tọa độ của điểm đó vào phương trình mặt phẳng, vế trái bằng 0.
Lời giải chi tiết:
Phương trình tổng quát của mặt phẳng \((\alpha )\):
Giả sử mặt phẳng \((\alpha )\) đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\). Phương trình mặt phẳng là:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc dưới dạng khác:
\(Ax + By + Cz + D = 0\)
với:
\(D = - (A{x_0} + B{y_0} + C{z_0})\)
Ý nghĩa điều kiện \(\vec n \cdot \overrightarrow {{M_0}M} = 0\):
Điều kiện này biểu diễn rằng tích vô hướng giữa vectơ pháp tuyến \(\vec n\) và vectơ \(\overrightarrow {{M_0}M} \) (nối từ \({M_0}\) đến một điểm bất kỳ \(M\)) bằng 0, có nghĩa là hai vectơ này vuông góc, đảm bảo rằng điểm \(M\) nằm trên mặt phẳng.
Trả lời câu hỏi Luyện tập 3 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tìm một vectơ pháp tuyến của các mặt phẳng sau:
a) \((\alpha ):x - 5y + 2 = 0;\)
b) \((\beta ):2y + 3 = 0.\)
Phương pháp giải:
Phương trình tổng quát của mặt phẳng trong không gian Oxyz có dạng:
\(Ax + By + Cz + D = 0\)
Vectơ pháp tuyến của mặt phẳng này là \(\vec n = (A,B,C)\), trong đó \(A\), \(B\), \(C\) là các hệ số của \(x\), \(y\), \(z\) trong phương trình.
Lời giải chi tiết:
a) Mặt phẳng \((\alpha ):x - 5y + 2 = 0\).
So sánh với phương trình tổng quát \(Ax + By + Cz + D = 0\), ta có:
\(A = 1,\quad B = - 5,\quad C = 0\)
Do đó, vectơ pháp tuyến của mặt phẳng \((\alpha )\) là:
\(\overrightarrow {{n_\alpha }} = (1, - 5,0)\)
b) Mặt phẳng \((\beta ):2y + 3 = 0\).
So sánh với phương trình tổng quát \(Ax + By + Cz + D = 0\), ta có:
\(A = 0,\quad B = 2,\quad C = 0\)
Do đó, vectơ pháp tuyến của mặt phẳng \((\beta )\) là:
\(\overrightarrow {{n_\beta }} = (0,2,0)\)
Trả lời câu hỏi Luyện tập 4 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(M(1;1;1)\), \(N(4;3;2)\), \(P(5;2;1)\). Viết phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P\) và vuông góc với \(MN\).
Phương pháp giải:
- Tìm vectơ chỉ phương của đường thẳng \(MN\) bằng cách lấy hiệu tọa độ của \(N\) và \(M\):
\(\overrightarrow {MN} = N - M\)
- Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là chính vectơ chỉ phương của đường thẳng \(MN\), vì mặt phẳng vuông góc với đường thẳng này.
- Phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\) có dạng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
Tính vectơ chỉ phương của \(MN\):
\(\overrightarrow {MN} = N - M = (4 - 1,3 - 1,2 - 1) = (3,2,1)\)
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n = (3,2,1)\).
Phương trình tổng quát của mặt phẳng \((\alpha )\) đi qua điểm \(P(5;2;1)\) có dạng:
\(3(x - 5) + 2(y - 2) + 1(z - 1) = 0\)
Khai triển biểu thức trên:
\(3x - 15 + 2y - 4 + z - 1 = 0\)
\(3x + 2y + z - 20 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((\alpha )\) là:
\(3x + 2y + z - 20 = 0\)
Trả lời câu hỏi Hoạt động 4 trang 44 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho mặt phẳng \((P)\) đi qua điểm \(M(2; - 1;3)\) và có cặp vectơ chỉ phương \(\vec a = (2;1; - 2)\), \(\vec b = (2; - 1;0)\).
a) Tìm \([\vec a,\vec b]\), và một vectơ pháp tuyến của \((P)\)
b) Viết phương trình tổng quát của mặt phẳng \((P)\).
Phương pháp giải:
- Tính tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) để tìm vectơ pháp tuyến của mặt phẳng \((P)\). Công thức tính tích có hướng:
\(\vec n = \vec a \times \vec b = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\)
- Sử dụng phương trình tổng quát của mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
Tính tích có hướng \(\vec n = \vec a \times \vec b\):
\(\vec n = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\2&1&{ - 2}\\2&{ - 1}&0\end{array}} \right|\)
Tính từng bước:
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 1}&0\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}2&{ - 2}\\2&0\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}2&1\\2&{ - 1}\end{array}} \right|\)
\( = {\bf{i}}(1 \cdot 0 - ( - 2) \cdot ( - 1)) - {\bf{j}}(2 \cdot 0 - ( - 2) \cdot 2) + {\bf{k}}(2 \cdot ( - 1) - 1 \cdot 2)\)
\( = {\bf{i}}(0 - 2) - {\bf{j}}(0 + 4) + {\bf{k}}( - 2 - 2)\)
\( = ( - 2, - 4, - 4)\)
Vậy vectơ pháp tuyến của mặt phẳng \((P)\) là:
\(\vec n = ( - 2, - 4, - 4)\)
Viết phương trình tổng quát của mặt phẳng \((P)\) đi qua điểm \(M(2; - 1;3)\):
\( - 2(x - 2) - 4(y + 1) - 4(z - 3) = 0\)
Khai triển:
\( - 2x + 4 - 4y - 4 - 4z + 12 = 0\)
\( - 2x - 4y - 4z + 12 = 0\)
Chia cả hai vế cho \( - 2\):
\(x + 2y + 2z - 6 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((P)\) là:
\(x + 2y + 2z - 6 = 0\)
Trả lời câu hỏi Luyện tập 5 trang 45 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba vectơ \(\vec a = (1; - 2;3)\), \(\vec b = (3;2; - 1)\), \(\vec c = ( - 2;4; - 6)\) và điểm \(A(4;1;0)\). Viết phương trình tổng quát của các mặt phẳng đi qua \(A\) và nhận hai trong ba vectơ \(\vec a,\vec b,\vec c\) làm cặp vectơ chỉ phương.
Phương pháp giải:
1. Chọn hai vectơ chỉ phương từ ba vectơ \(\vec a,\vec b,\vec c\).
2. Tìm tích có hướng của hai vectơ đã chọn để tìm vectơ pháp tuyến của mặt phẳng.
3. Viết phương trình tổng quát của mặt phẳng đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vectơ pháp tuyến \(\vec n = (A;B;C)\):
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
- Mặt phẳng thứ nhất chứa \(\vec a\) và \(\vec b\):
Tích có hướng của \(\vec a\) và \(\vec b\):
\({\vec n_1} = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 2}&3\\2&{ - 1}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}1&3\\3&{ - 1}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\3&2\end{array}} \right|\)
\( = {\bf{i}}(\left( { - 2} \right) \cdot ( - 1) - 3 \cdot 2) - {\bf{j}}(1 \cdot ( - 1) - 3 \cdot 3) + {\bf{k}}(1 \cdot 2 - ( - 2) \cdot 3)\)
\( = {\bf{i}}( - 2 - 6) - {\bf{j}}( - 1 - 9) + {\bf{k}}(2 + 6)\)
\( = ( - 4,10,8)\)
Vậy vectơ pháp tuyến của mặt phẳng 1 là \({\vec n_1} = ( - 4,10,8)\). 2. Viết phương trình tổng quát của mặt phẳng 1 đi qua điểm \(A(4;1;0)\):
\( - 4(x - 4) + 10(y - 1) + 8(z - 0) = 0\)
\( - 4x + 16 + 10y - 10 + 8z = 0\)
\( - 4x + 10y + 8z + 6 = 0\)
Vậy phương trình tổng quát của mặt phẳng thứ nhất là:
\( - 4x + 10y + 8z + 6 = 0\)
- Mặt phẳng thứ hai chứa \(\vec a\) và \(\vec c\):
Tích có hướng của \(\vec a\) và \(\vec c\):
\({\vec n_2} = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 2}&3\\4&{ - 6}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}1&3\\{ - 2}&{ - 6}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 2}&4\end{array}} \right|\)
\( = {\bf{i}}(( - 2) \cdot ( - 6) - 3 \cdot 4) - {\bf{j}}(1 \cdot ( - 6) - 3 \cdot ( - 2)) + {\bf{k}}(1 \cdot 4 - ( - 2) \cdot ( - 2))\)
\( = {\bf{i}}(12 - 12) - {\bf{j}}( - 6 + 6) + {\bf{k}}(4 - 4)\)
\( = (0,0,0)\)
Kết quả cho thấy hai vectơ \(\vec a\) và \(\vec c\) cùng phương, nên không tạo thành mặt phẳng mới. Chúng ta không cần xét tiếp trường hợp này.
- Mặt phẳng thứ 3 chứa \(\vec b\) và \(\vec c\):
Tích có hướng của \(\vec b\) và \(\vec c\):
\({\vec n_3} = {\bf{i}}\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 6}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}3&{ - 1}\\{ - 2}&{ - 6}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}3&2\\{ - 2}&4\end{array}} \right|\)
\( = {\bf{i}}(2 \cdot ( - 6) - ( - 1) \cdot 4) - {\bf{j}}(3 \cdot ( - 6) - ( - 1) \cdot ( - 2)) + {\bf{k}}(3 \cdot 4 - 2 \cdot ( - 2))\)
\( = {\bf{i}}( - 12 + 4) - {\bf{j}}( - 18 - 2) + {\bf{k}}(12 + 4)\)
\( = ( - 8, - 20,16)\)
Vậy vectơ pháp tuyến của mặt phẳng 3 là \({\vec n_3} = ( - 8, - 20,16)\). 2. Viết phương trình tổng quát của mặt phẳng 3 đi qua điểm \(A(4;1;0)\):
\( - 8(x - 4) - 20(y - 1) + 16(z - 0) = 0\)
\( - 8x + 32 - 20y + 20 + 16z = 0\)
\( - 8x - 20y + 16z + 52 = 0\)
Vậy phương trình tổng quát của mặt phẳng thứ 3 là:
\( - 8x - 20y + 16z + 52 = 0\)
Trả lời câu hỏi Hoạt động 5 trang 45 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho ba điểm \(A(4; - 1;2)\), \(B(1;4; - 3)\), \(C(3; - 4;7)\).
a) Chứng minh ba điểm \(A\), \(B\), \(C\) không thẳng hàng.
b) Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \((ABC)\).
c) Viết phương trình tổng quát của mặt phẳng \((ABC)\).
Phương pháp giải:
1. Để chứng minh ba điểm \(A\), \(B\), \(C\) không thẳng hàng, tính hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Nếu hai vectơ này không cùng phương thì ba điểm không thẳng hàng.
2. Tìm tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) để tìm vectơ pháp tuyến của mặt phẳng.
3. Sử dụng phương trình tổng quát của mặt phẳng:
\(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\)
hoặc
\(Ax + By + Cz + D = 0\)
với \(D = - (A{x_0} + B{y_0} + C{z_0})\).
Lời giải chi tiết:
a) Tính các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = B - A = (1 - 4,4 + 1, - 3 - 2) = ( - 3,5, - 5)\)
\(\overrightarrow {AC} = C - A = (3 - 4, - 4 + 1,7 - 2) = ( - 1, - 3,5)\)
Xét tỉ số giữa các tọa độ của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\frac{{ - 3}}{{ - 1}} = 3,\quad \frac{5}{{ - 3}} = - \frac{5}{3},\quad \frac{{ - 5}}{5} = - 1\)
Các tỉ số không bằng nhau, nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương. Do đó, ba điểm \(A\), \(B\), \(C\) không thẳng hàng.
b) Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\vec n = {\bf{i}}\left| {\begin{array}{*{20}{c}}5&{ - 5}\\{ - 3}&5\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}{ - 3}&{ - 5}\\{ - 1}&5\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}{ - 3}&5\\{ - 1}&{ - 3}\end{array}} \right|\)
\( = {\bf{i}}(5 \cdot 5 - ( - 5) \cdot ( - 3)) - {\bf{j}}(( - 3) \cdot 5 - ( - 5) \cdot ( - 1)) + {\bf{k}}(( - 3) \cdot ( - 3) - 5 \cdot ( - 1))\)
\( = {\bf{i}}(25 - 15) - {\bf{j}}(( - 15 - 5)) + {\bf{k}}(9 + 5)\)
\( = (10,20,14)\)
Vậy vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\vec n = (10,20,14)\).
c) Viết phương trình tổng quát của mặt phẳng đi qua điểm \(A(4; - 1;2)\):
\(10(x - 4) + 20(y + 1) + 14(z - 2) = 0\)
\(10x - 40 + 20y + 20 + 14z - 28 = 0\)
\(10x + 20y + 14z - 48 = 0\)
Vậy phương trình tổng quát của mặt phẳng \((ABC)\) là:
\(10x + 20y + 14z - 48 = 0\)
Trả lời câu hỏi Luyện tập 6 trang 46 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, cho bốn điểm \(A(4;0;0)\), \(B(0; - 5;0)\), \(C(0;0;6)\), \(D( - 5;3;4)\). Viết phương trình các mặt phẳng \((ABC)\), \((BCD)\), \((ABD)\), \((ACD)\).
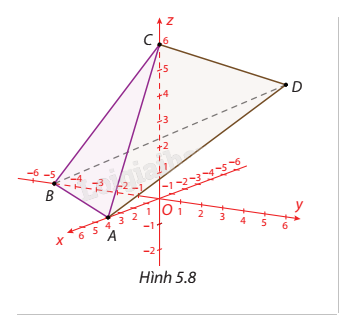
Phương pháp giải:
1. Xác định các vectơ chỉ phương từ các điểm đã cho. Ví dụ, để viết phương trình mặt phẳng \((ABC)\), ta tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
2. Tìm vectơ pháp tuyến của mặt phẳng bằng cách lấy tích có hướng của hai vectơ chỉ phương vừa tìm được.
3. Sử dụng phương trình tổng quát của mặt phẳng:
\(Ax + By + Cz + D = 0\)
với \((A,B,C)\) là tọa độ của vectơ pháp tuyến và \(D = - (A{x_0} + B{y_0} + C{z_0})\), trong đó \(({x_0},{y_0},{z_0})\) là tọa độ của một điểm thuộc mặt phẳng.
Lời giải chi tiết:
1. Phương trình mặt phẳng \((ABC)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\overrightarrow {AB} = B - A = (0 - 4, - 5 - 0,0 - 0) = ( - 4, - 5,0)\)
\(\overrightarrow {AC} = C - A = (0 - 4,0 - 0,6 - 0) = ( - 4,0,6)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \):
\(\left( {( - 5).6 - 0.0,0.( - 4) - ( - 4).6,( - 4).0 - ( - 5).( - 4)} \right)\)
\( = ( - 30,24, - 20)\)
Phương trình mặt phẳng \((ABC)\) là:
\( - 30(x - 4) + 24(y - 0) - 20(z - 0) = 0\)
\( - 30x + 120 + 24y - 20z = 0\)
\(30x - 24y + 20z = 120\)
Vậy phương trình mặt phẳng \((ABC)\) là:
\(30x - 24y + 20z = 120\)
2. Phương trình mặt phẳng \((BCD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \):
\(\overrightarrow {BC} = C - B = (0 - 0,0 - ( - 5),6 - 0) = (0,5,6)\)
\(\overrightarrow {BD} = D - B = ( - 5 - 0,3 - ( - 5),4 - 0) = ( - 5,8,4)\)
Tích có hướng của \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \):
\(\left( {5.4 - 6.8,6.( - 5) - 0.4,0.8 - ( - 5).5} \right)\)
\( = ( - 28, - 30,25)\)
Phương trình mặt phẳng \((BCD)\) là:
\( - 28(x - 0) - 30(y + 5) + 25(z - 0) = 0\)
\( - 28x - 30y - 150 + 25z = 0\)
\(28x + 30y - 25z = - 150\)
Vậy phương trình mặt phẳng \((BCD)\) là:
\(28x + 30y - 25z = - 150\)
3. Phương trình mặt phẳng \((ABD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AB} = ( - 4, - 5,0)\)
\(\overrightarrow {AD} = D - A = ( - 5 - 4,3 - 0,4 - 0) = ( - 9,3,4)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\left( {( - 5).4 - 0.3,\,\,0.( - 9) - ( - 4).4,\,\,( - 4).3 - ( - 5).( - 9)} \right)\)
\( = ( - 20,16, - 57)\)
Phương trình mặt phẳng \((ABD)\) là:
\( - 20(x - 4) + 16(y - 0) - 57(z - 0) = 0\)
\( - 20x + 80 + 16y - 57z = 0\)
\(20x - 16y + 57z = 80\)
Vậy phương trình mặt phẳng \((ABD)\) là:
\(20x - 16y + 57z = 80\)
4. Phương trình mặt phẳng \((ACD)\):
Tính hai vectơ chỉ phương \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AC} = ( - 4,0,6)\)
\(\overrightarrow {AD} = ( - 9,3,4)\)
Tích có hướng của \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \):
\(\left( {0.4 - 6.3,\,\,6.( - 9) - ( - 4).4,\,\,( - 4).3 - 0.( - 9)} \right)\)
\(( - 18, - 38, - 12)\)
Phương trình mặt phẳng \((ACD)\) là:
\( - 18(x - 4) - 38(y - 0) - 12(z - 0) = 0\)
\( - 18x + 72 - 38y - 12z = 0\)
\(18x + 38y + 12z = 72\)
Vậy phương trình mặt phẳng \((ACD)\) là:
\(18x + 38y + 12z = 72\)
Trả lời câu hỏi Vận dụng 1 trang 46 SGK Toán 12 Cùng khám phá
Một phần sân nhà bác An có dạng hình thang \(ABCD\) vuông tại \(A\) và \(B\) với độ dài \(AB = 9{\mkern 1mu} m\), \(AD = 5{\mkern 1mu} m\) và \(BC = 6{\mkern 1mu} m\) như Hình 5.9. Theo thiết kế ban đầu thì mặt sân bằng phẳng và các điểm \(A\), \(B\), \(C\), \(D\) có độ cao như nhau. Sau đó bác An thay đổi thiết kế để nước có thể thoát về phía góc sân ở vị trí \(C\) bằng cách giữ nguyên độ cao ở \(A\), giảm độ cao của sân ở vị trí \(B\) và \(D\) xuống thấp hơn độ cao ở \(A\) lần lượt là \(6{\mkern 1mu} cm\) và \(3,6{\mkern 1mu} cm\). Để mặt sân sau khi lát gạch vẫn là bề mặt phẳng thì bác An cần phải giảm độ cao ở \(C\) xuống bao nhiêu centimet so với độ cao ở \(A\)?
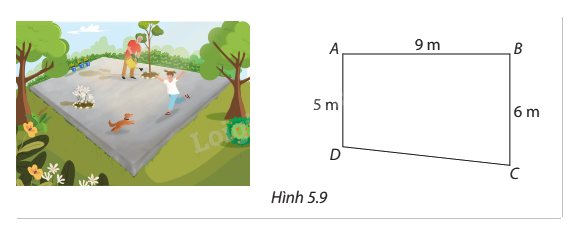
Phương pháp giải:
- Ta coi các độ cao là tọa độ \(z\) của các điểm \(A\), \(B\), \(C\), \(D\) trong không gian. Do độ cao của điểm \(A\) không thay đổi, ta đặt \({z_A} = 0\). Giả sử các tọa độ khác của các điểm là tọa độ trong mặt phẳng \(Oxy\), ta có:
\(A(0;0;0),\quad B(9;0; - 0,06),\quad D(0;5; - 0,036),\quad C({x_C};{y_C};{z_C})\)
- Xác định phương trình mặt phẳng chứa các điểm \(A\), \(B\), \(D\) (vì mặt phẳng này là phẳng nên tọa độ \(z\) của \(C\) phải thỏa mãn phương trình này).
- Tìm tọa độ \({z_C}\) bằng cách giải hệ phương trình.
Lời giải chi tiết:
Gọi độ cao của các điểm \(A,B,C,D\)lần lượt là \({z_A}\), \({z_B}\), \({z_C}\), \({z_D}\). Theo đề bài, ta có:
\({z_A} = {z_B} = {z_D} = 0.\)
Sau khi điều chỉnh, độ cao của các điểm \(B,D\) được thay đổi như sau:
\({z_B} = - 0,06{\mkern 1mu} {\rm{m}},\quad {z_D} = - 0,036{\mkern 1mu} {\rm{m}}.\)
Để mặt sân sau khi lát gạch là một mặt phẳng, ta cần lập phương trình mặt phẳng \((ABCD)\) đi qua ba điểm \(A(0;0;0)\), \(B(9;0; - 0,06)\), \(D(0;5; - 0,036)\). Phương trình mặt phẳng có dạng:
\(Ax + By + Cz + D = 0.\)
Vì mặt phẳng đi qua \(A(0;0;0)\), thay \(A(0;0;0)\) vào phương trình ta được:
\(D = 0.\)
Do đó, phương trình mặt phẳng có dạng:
\(Ax + By + Cz = 0.\)
Tính hai vectơ chỉ phương \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\overrightarrow {AB} = (9;0; - 0,06)\)
\(\overrightarrow {AD} = \left( {0;5; - 0,036} \right)\)
Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \):
\(\left( {0.( - 0,036) - ( - 0,06).5;( - 0,06).0 - 9.( - 0,036);9.5 - 0.0} \right)\)
\( = (0,3;0,324;45)\)
Ta có phương trình mặt phẳng:
\(0,3x + 0,324y + 45z = 0\)
Thay tọa độ \(C(9;6;{z_C})\) vào phương trình:
\(0,3.(9) + 0,324.(6) + 45{z_C} = 0\)
\(2,7 + 1,944 + 45{z_C} = 0\)
\({z_C} = - 0,1032{\mkern 1mu} {\rm{m}}\)
Vậy độ cao của điểm \(C\) cần giảm là:
\({z_C} = - 0.1032{\mkern 1mu} {\rm{m}} = - 10.32{\mkern 1mu} {\rm{cm}}.\)
Bác An cần hạ độ cao của điểm \(C\) xuống khoảng \(10.32{\mkern 1mu} {\rm{cm}}\) so với độ cao của điểm \(A\).
Giải mục 2 trang 43, 44, 45, 46 SGK Toán 12 tập 2: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 2 thường tập trung vào các ứng dụng của tích phân, đặc biệt là tính diện tích hình phẳng. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các kiến thức cơ bản về tích phân xác định, phương pháp tính tích phân và các công thức tính diện tích hình phẳng giới hạn bởi các đường cong.
Các kiến thức trọng tâm cần nắm vững:
- Tích phân xác định: Định nghĩa, tính chất, các phương pháp tính tích phân (đổi biến, tích phân từng phần).
- Ứng dụng của tích phân: Tính diện tích hình phẳng, tính thể tích vật thể tròn xoay.
- Diện tích hình phẳng: Công thức tính diện tích hình phẳng giới hạn bởi các đường cong y = f(x), trục Ox, và hai đường thẳng x = a, x = b.
Giải chi tiết các bài tập trang 43, 44, 45, 46
Trang 43: Bài tập về tính diện tích hình phẳng đơn giản
Các bài tập trên trang 43 thường yêu cầu tính diện tích hình phẳng giới hạn bởi các đường cong đơn giản và trục Ox. Để giải các bài tập này, học sinh cần xác định chính xác các điểm giao nhau giữa đường cong và trục Ox, sau đó áp dụng công thức tính diện tích tích phân.
Trang 44: Bài tập về tính diện tích hình phẳng phức tạp hơn
Trang 44 giới thiệu các bài tập phức tạp hơn, trong đó hình phẳng được giới hạn bởi nhiều đường cong. Để giải các bài tập này, học sinh cần chia hình phẳng thành các phần nhỏ hơn, tính diện tích của từng phần, và cộng lại để được diện tích tổng.
Trang 45: Bài tập về ứng dụng tích phân trong thực tế
Các bài tập trên trang 45 thường liên quan đến các ứng dụng thực tế của tích phân, chẳng hạn như tính diện tích của một mảnh đất có hình dạng phức tạp. Để giải các bài tập này, học sinh cần mô hình hóa bài toán bằng các hàm số và tích phân.
Trang 46: Bài tập tổng hợp và nâng cao
Trang 46 chứa các bài tập tổng hợp và nâng cao, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết. Các bài tập này thường có tính chất thách thức và giúp học sinh rèn luyện tư duy toán học.
Lời khuyên khi giải bài tập
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán trước khi bắt đầu giải.
- Vẽ hình minh họa: Vẽ hình minh họa giúp hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Tham khảo các nguồn tài liệu khác: Nếu gặp khó khăn, hãy tham khảo các nguồn tài liệu khác như sách giáo khoa, sách bài tập, hoặc các trang web học tập trực tuyến.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn tự hào là một trong những trang web cung cấp lời giải bài tập Toán 12 tập 2 đầy đủ và chính xác nhất. Chúng tôi luôn cập nhật những lời giải mới nhất và cung cấp các bài giảng chi tiết, dễ hiểu để giúp các em học sinh học tập hiệu quả.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!