Lý thuyết Phương trình mặt cầu Toán 12 Cùng khám phá
Tổng quan nội dung
Lý Thuyết Phương Trình Mặt Cầu Toán 12 - Nền Tảng Quan Trọng
Phương trình mặt cầu là một trong những kiến thức trọng tâm của chương trình Hình học không gian lớp 12. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các bài toán nâng cao và các kỳ thi quan trọng.
Tại tusach.vn, chúng tôi cung cấp tài liệu học tập đầy đủ và dễ hiểu về phương trình mặt cầu, giúp bạn tự tin chinh phục môn Toán.
1. Định nghĩa mặt cầu
1. Định nghĩa mặt cầu
| Tập hợp tất cả các điểm trong không gian cách điểm I cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm I bán kính r, kí hiệu S(I;r) hay (S). |
Lưu ý: Cho mặt cầu S(I;r) và điểm M bất kì trong không gian.
- Nếu IM = r thì M nằm trên mặt cầu S(I;r).
- Nếu IM < r thì M nằm ngoài mặt cầu S(I;r).
- Nếu IM > r thì M nằm ngoài mặt cầu S(I;r).
Ví dụ:
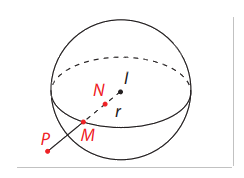
- Điểm M nằm trên mặt cầu (S). - Điểm N nằm trong mặt cầu (S). - Điểm P nằm ngoài mặt cầu (S).
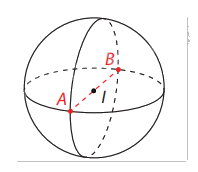
- Nếu hai điểm A, B nằm trên mặt cầu S(I;r) và đoạn thẳng AB đi qua tâm I thì AB được gọi là một đường kính của mặt cầu. Khi đó độ dài đường kính bằng 2r. - Một mặt cầu được xác định khi ta biết tâm và bán kính hoặc biết một đường kính của nó.
Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu tâm I(-2;1;5) bán kính 3. Các điểm A(10;1;2), B(0;1;4), C(0;3;4) nằm trong, nằm trên hay nằm ngoài mặt cầu đó?
Giải:
Do \(IA = \sqrt {{{\left( {10 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}} = \sqrt {153} > 3\) nên điểm A(10;1;2) nằm ngoài mặt cầu đó.
Do \(IB = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 5 < 3\) nên điểm B(0;1;4) nằm trong mặt cầu đó.
Do \(IC = \sqrt {{{\left( {0 - ( - 2)} \right)}^2} + {{\left( {3 - 1} \right)}^2} + {{\left( {4 - 5} \right)}^2}} = \sqrt 9 = 3\) nên điểm C(0;3;4) nằm trên mặt cầu đó.
2. Phương trình mặt cầu
Phương trình của mặt cầu tâm I(a;b;c) bán kính r là \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\). |
Ví dụ 1: Trong không gian Oxyz, xác định tâm I và bán kính r của mặt cầu có phương trình:
a) \({(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16\).
b) \({(x + 2)^2} + {y^2} + {(z + 3)^2} = 4\).
Giải:
a) Ta có \({(x - 1)^2} + {(y + 2)^2} + {(z - 3)^2} = 16 \Leftrightarrow {(x - 1)^2} + {(y - ( - 2))^2} + {(z - 3)^2} = {4^2}\).
Vậy đây là phương trình mặt cầu có tâm I(1;-2;3) và bán kính r = 4.
b) Ta có \({(x + 2)^2} + {y^2} + {(z + 3)^2} = 4 \Leftrightarrow {(x - ( - 2))^2} + {(y - 0)^2} + {(z - ( - 3))^2} = {2^2}\).
Vậy đây là phương trình mặt cầu có tâm I(-2;0;-3) và bán kính r = 2.
Ví dụ 2: Viết phương trình mặt cầu, biết:
a) Có tâm I(1;2;3), bán kính R = 10.
b) Có tâm I(3;-1;-5) và đi qua điểm B(0;2;1).
Giải:
a) Phương trình của mặt cầu tâm I(1;2;3) bán kính R = 10 là \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 100\).
b) Bán kính mặt cầu là \(R = IB = \sqrt {{{(0 - 3)}^2} + {{(2 + 1)}^2} + {{(1 + 5)}^2}} = \sqrt {54} \).
Phương trình mặt cầu tâm I(3;-1;-5) bán kính \(R = \sqrt {54} \) là \({(x - 3)^2} + {(y + 1)^2} + {(z + 5)^3} = 54\).
Nhận xét:
Cho mặt cầu tâm I(a;b;c) bán kính r có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {r^2}\). Ta có thể viết phương trình đó dưới dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\), với \(d = {a^2} + {b^2} + {c^2} - {R^2}\).
Dạng phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) xác định một mặt cầu khi và chỉ khi \({a^2} + {b^2} + {c^2} - d > 0\) với tâm I(a;b;c) và bán kính \(r = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Ví dụ 3: Mỗi phương tình sau có là phương trình mặt cầu hay không? Vì sao?
a) \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\).
b) \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\).
Giải:
a) Phương trình \(2{x^2} + {y^2} + {z^2} - 2x - 2y + 2z + 1 = 0\) không phải phương trình mặt cầu vì hệ số của \({x^2}\) và \({y^2}\) khác nhau.
b) Phương trình \({x^2} + {y^2} - 2x + 6y - 8z - 3 = 0\) không phải phương trình mặt cầu vì không có biểu thức \({z^2}\).
Ví dụ 4: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\).
b) \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\).
Giải:
a) Phương trình \({x^2} + {y^2} + {z^2} - 4x + 10y - 2z + 14 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = 2;b = - 5;c = 1;d = 14\).
Ta có \({a^2} + {b^2} + {c^2} - d = 4 + 25 + 1 - 14 = 16 > 0\).
Suy ra phương trình đã cho là phương trình mặt cầu tâm I(2;-5;1), bán kính R = 4.
b) Phương trình \({x^2} + {y^2} + {z^2} + 2x + 4y - 6z + 20 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - 1;b = - 2;c = 3;d = 20\).
Ta có \({a^2} + {b^2} + {c^2} - d = 1 + 4 + 9 - 20 = - 6 < 0\).
Suy ra phương trình đã cho không phải phương trình mặt cầu.
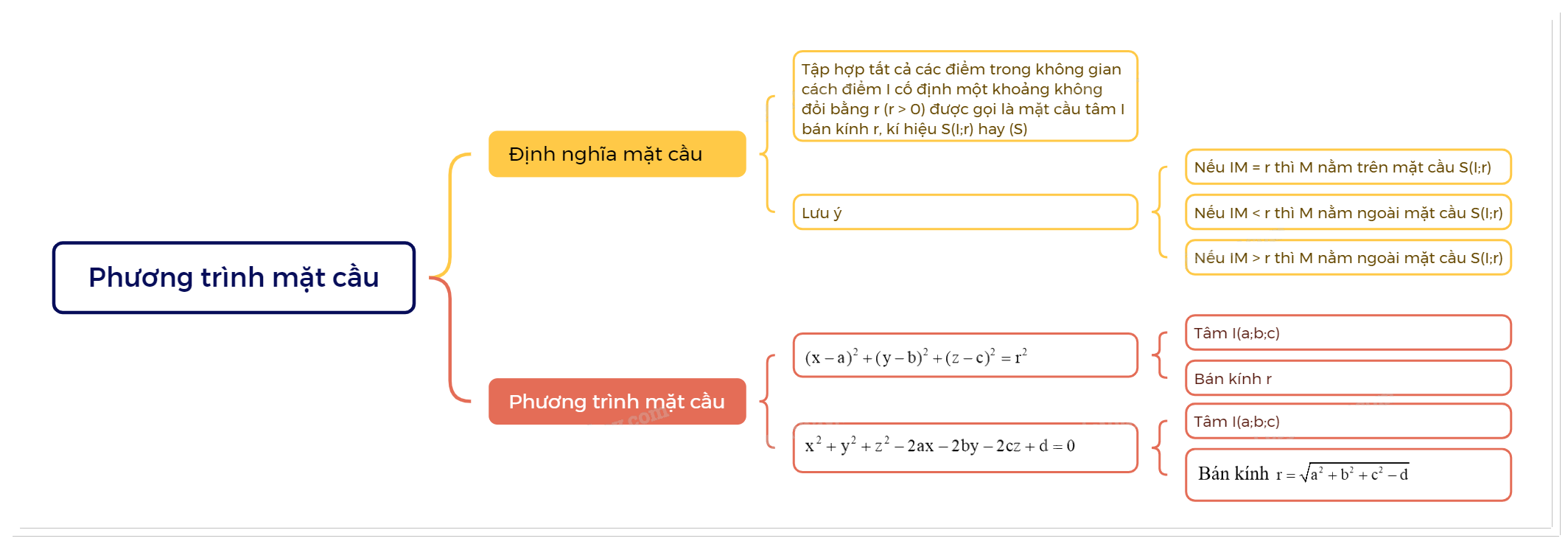
Lý Thuyết Phương Trình Mặt Cầu Toán 12: Tổng Quan Chi Tiết
Phương trình mặt cầu là một phần quan trọng trong chương trình Hình học không gian lớp 12. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết này, bao gồm định nghĩa, các dạng phương trình, cách xác định tâm và bán kính của mặt cầu, cũng như các ứng dụng thực tế.
1. Định Nghĩa Mặt Cầu và Phương Trình Mặt Cầu
Mặt cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính). Công thức tổng quát của phương trình mặt cầu trong không gian Oxyz là:
(x - a)2 + (y - b)2 + (z - c)2 = R2
Trong đó:
- (a, b, c) là tọa độ tâm của mặt cầu.
- R là bán kính của mặt cầu.
2. Các Dạng Phương Trình Mặt Cầu
Ngoài dạng phương trình tổng quát, phương trình mặt cầu còn có thể được biểu diễn dưới các dạng khác:
- Phương trình chính tắc: Khi tâm mặt cầu trùng với gốc tọa độ O(0, 0, 0), phương trình trở thành: x2 + y2 + z2 = R2
- Phương trình mặt cầu có tâm I(x0, y0, z0) và bán kính R: (x - x0)2 + (y - y0)2 + (z - z0)2 = R2
3. Xác Định Tâm và Bán Kính Mặt Cầu
Từ phương trình mặt cầu (x - a)2 + (y - b)2 + (z - c)2 = R2, ta có thể dễ dàng xác định:
- Tâm mặt cầu: I(a, b, c)
- Bán kính mặt cầu: R = √R2
4. Các Bài Toán Liên Quan Đến Phương Trình Mặt Cầu
Một số bài toán thường gặp liên quan đến phương trình mặt cầu:
- Viết phương trình mặt cầu khi biết tâm và bán kính.
- Xác định tâm và bán kính của mặt cầu từ phương trình.
- Kiểm tra một điểm có nằm trên mặt cầu hay không.
- Tìm giao điểm của mặt cầu với các đường thẳng, mặt phẳng.
5. Ví Dụ Minh Họa
Ví dụ 1: Viết phương trình mặt cầu có tâm I(1, -2, 3) và bán kính R = 5.
Giải: Phương trình mặt cầu là: (x - 1)2 + (y + 2)2 + (z - 3)2 = 25
Ví dụ 2: Xác định tâm và bán kính của mặt cầu có phương trình: x2 + y2 + z2 - 2x + 4y - 6z + 5 = 0
Giải: Biến đổi phương trình về dạng chính tắc:
(x2 - 2x + 1) + (y2 + 4y + 4) + (z2 - 6z + 9) = -5 + 1 + 4 + 9
(x - 1)2 + (y + 2)2 + (z - 3)2 = 9
Vậy tâm mặt cầu là I(1, -2, 3) và bán kính R = 3.
6. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững lý thuyết phương trình mặt cầu, bạn nên luyện tập thêm nhiều bài tập khác nhau. Tusach.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Bảng tổng hợp các công thức quan trọng:
| Công thức | Mô tả |
|---|---|
| (x - a)2 + (y - b)2 + (z - c)2 = R2 | Phương trình mặt cầu |
| x2 + y2 + z2 = R2 | Phương trình mặt cầu tâm O |
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết phương trình mặt cầu Toán 12. Chúc bạn học tập tốt và đạt kết quả cao!