Giải bài tập 5.43 trang 86 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 5.43 Trang 86 Toán 12 Tập 2
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5.43 trang 86 SGK Toán 12 tập 2. Bài tập này thuộc chương trình học về số phức và các phép toán liên quan.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
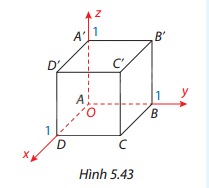
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, với A(0; 0; 0), D(1; 0; 0), B(0; 1; 0), A’(0; 0; 1). a) Chứng minh \(A'C \bot (AB'D')\). b) Chứng minh \((AB'D')//(C'BD)\)và tính khoảng cách giữa hai mặt phẳng \((AB'D')\) và \((C'BD)\). c) Tính côsin của góc giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\).
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, với A(0; 0; 0), D(1; 0; 0), B(0; 1; 0), A’(0; 0; 1).
a) Chứng minh \(A'C \bot (AB'D')\).
b) Chứng minh \((AB'D')//(C'BD)\)và tính khoảng cách giữa hai mặt phẳng \((AB'D')\) và \((C'BD)\).
c) Tính côsin của góc giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\).
Phương pháp giải - Xem chi tiết
a) Chứng minh đường thẳng vuông góc với mặt phẳng:
- Tìm véc-tơ pháp tuyến của mặt phẳng bằng tích có hướng của hai véc-tơ trong mặt phẳng.
- Kiểm tra tích vô hướng giữa véc-tơ chỉ phương của đường thẳng và véc-tơ pháp tuyến của mặt phẳng. Nếu tích vô hướng bằng 0, đường thẳng vuông góc với mặt phẳng.
b) Chứng minh hai mặt phẳng song song và tính khoảng cách:
- Tìm véc-tơ pháp tuyến của từng mặt phẳng. Nếu hai véc-tơ pháp tuyến cùng phương, hai mặt phẳng song song.
- Tính khoảng cách giữa hai mặt phẳng song song bằng công thức khoảng cách từ điểm đến mặt phẳng.
c) Tính góc giữa hai mặt phẳng:
- Tìm véc-tơ pháp tuyến của mỗi mặt phẳng.
- Dùng công thức để tính góc giữa hai mặt phẳng.
Lời giải chi tiết
Các đỉnh còn lại có toạ độ là: \(C(1;1;0)\), \(B'(0;1;1)\), \(C'(1;1;1)\), \(D'(1;0;1)\)
a) Chứng minh \(A'C \bot (AB'D')\)
Véc-tơ pháp tuyến của \((AB'D')\):
\(\overrightarrow {AB'} = (0;1;1),\quad \overrightarrow {AD'} = (1;0;1)\)
\({\vec n_{(AB'D')}} = \overrightarrow {AB'} \times \overrightarrow {AD'} = (1;1; - 1)\)
Mà ta có: \(\overrightarrow {A'C} = (1;1; - 1)\)trùng với vec-tơ pháp tuyến của \((AB'D')\)
Vậy \(A'C \bot (AB'D')\).
b) Chứng minh \((AB'D')\parallel (C'BD)\) và tính khoảng cách
Véc-tơ pháp tuyến của \((C'BD)\):
\(\overrightarrow {C'B} = ( - 1;0; - 1),\quad \overrightarrow {C'D} = (0; - 1; - 1)\)
\({\vec n_{(C'BD)}} = \overrightarrow {C'B} \times \overrightarrow {C'D} = ( - 1; - 1;1)\)
Hai véc-tơ pháp tuyến \({\vec n_{(AB'D')}}\) và \({\vec n_{(C'BD)}}\) cùng phương nên \((AB'D')\parallel (C'BD)\).
* Khoảng cách giữa hai mặt phẳng:
Chọn điểm \(A(0,0,0)\) thuộc \((AB'D')\).
Phương trình \((C'BD)\): \(1.(x - 0) - 1.(y - 1) - (z - 0) = 0 \Leftrightarrow x - y - z + 1 = 0\).
\(d = \frac{{|0 \cdot 1 - 0 \cdot 1 - 0 \cdot ( - 1) + 1|}}{{\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {1^2}} }} = \frac{1}{{\sqrt 3 }}\)
c) Tính \(\cos \theta \) giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\)
- Véc-tơ pháp tuyến của \((DA'C')\):
\(\overrightarrow {DA'} = ( - 1;0;1),\quad \overrightarrow {DC'} = (0;1;1)\)
\({\vec n_{(DA'C')}} = \overrightarrow {DA'} \times \overrightarrow {DC'} = ( - 1;1; - 1)\)
Véc-tơ pháp tuyến của \((ABB'A')\):
\(\overrightarrow {AB} = (0,1,0),\quad \overrightarrow {AA'} = (0,0,1)\)
\({\vec n_{(ABB'A')}} = \overrightarrow {AB} \times \overrightarrow {AA'} = (1,0,0)\)
Tính \(\cos \theta \):
\({\vec n_{(DA'C')}} \cdot {\vec n_{(ABB'A')}} = ( - 1;1; - 1) \cdot (1;0;0) = - 1\)
\(\cos \theta = \frac{{| - 1|}}{{\sqrt 3 \cdot 1}} = \frac{1}{{\sqrt 3 }}\)
Giải Bài Tập 5.43 Trang 86 Toán 12 Tập 2: Hướng Dẫn Chi Tiết
Bài tập 5.43 trang 86 SGK Toán 12 tập 2 yêu cầu chúng ta tìm số phức z thỏa mãn một điều kiện nhất định. Để giải bài tập này, chúng ta cần nắm vững kiến thức về số phức, bao gồm dạng đại số của số phức, các phép toán cộng, trừ, nhân, chia số phức, và đặc biệt là module của số phức.
Đề Bài Bài Tập 5.43 Trang 86 Toán 12 Tập 2
(Đề bài cụ thể của bài tập 5.43 sẽ được chèn vào đây. Ví dụ: Tìm số phức z biết |z - 1| = |z + 1| và |z| = 1.)
Phương Pháp Giải Bài Tập Về Số Phức
Để giải quyết các bài toán liên quan đến số phức, chúng ta có thể áp dụng các phương pháp sau:
- Biểu diễn số phức trên mặt phẳng phức: Sử dụng mặt phẳng phức để hình dung các số phức và các phép toán trên chúng.
- Sử dụng dạng đại số của số phức: Đặt z = a + bi, với a, b là các số thực, và thực hiện các phép toán trên các số thực a và b.
- Sử dụng các công thức liên quan đến module của số phức: |z| = √(a² + b²), |z₁ + z₂| ≤ |z₁| + |z₂|, |z₁ - z₂| ≥ ||z₁| - |z₂||.
- Sử dụng các tính chất của số phức liên hợp: z̄ = a - bi, |z| = |z̄|, z + z̄ = 2a, z * z̄ = a² + b².
Lời Giải Chi Tiết Bài Tập 5.43 Trang 86 Toán 12 Tập 2
(Lời giải chi tiết của bài tập 5.43 sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ:
- Đặt z = a + bi, với a, b là các số thực.
- Thay z vào phương trình |z - 1| = |z + 1| và rút gọn.
- Thay z vào phương trình |z| = 1 và rút gọn.
- Giải hệ phương trình để tìm a và b.
- Kết luận giá trị của z.
)
Ví Dụ Minh Họa
Để hiểu rõ hơn về cách giải bài tập về số phức, chúng ta hãy xem xét một ví dụ sau:
(Ví dụ minh họa về một bài tập tương tự sẽ được trình bày ở đây, kèm theo lời giải chi tiết.)
Luyện Tập Thêm
Để củng cố kiến thức và kỹ năng giải bài tập về số phức, các em có thể luyện tập thêm với các bài tập sau:
- Bài tập 5.44 trang 86 SGK Toán 12 tập 2
- Bài tập 5.45 trang 86 SGK Toán 12 tập 2
- Các bài tập trắc nghiệm về số phức
Tổng Kết
Bài tập 5.43 trang 86 SGK Toán 12 tập 2 là một bài tập điển hình về số phức. Việc nắm vững kiến thức về số phức và các phương pháp giải bài tập sẽ giúp các em giải quyết các bài toán tương tự một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!
Nguồn tham khảo:
- Sách giáo khoa Toán 12 tập 2
- Các trang web học Toán trực tuyến uy tín