Lý Thuyết Vectơ Không Gian Toán 12 - tusach.vn

Lý thuyết Các phép toán vecto trong không gian Toán 12 Cùng khám phá

Lý thuyết Các phép toán vectơ trong không gian Toán 12

Chào mừng bạn đến với bài học lý thuyết về các phép toán vectơ trong không gian, một phần kiến thức quan trọng trong chương trình Toán 12.

Bài viết này sẽ cung cấp một cách hệ thống và dễ hiểu về các khái niệm cơ bản, các phép toán và ứng dụng của vectơ trong không gian.

Chúng ta sẽ cùng nhau khám phá cách thực hiện cộng, trừ vectơ, tích vô hướng, tích có hướng và các ứng dụng thực tế của chúng.

1. Tổng và hiệu của hai vecto trong không gian a) Tổng của hai vecto

1. Tổng và hiệu của hai vecto trong không gian

a) Tổng của hai vecto

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \).

Phép lấy tổng của hai vecto được gọi là phép cộng vecto.

- Với 3 điểm A, B, C trong không gian, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (Quy tắc 3 điểm).

- Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (Quy tắc hình bình hành).

- Nếu ABCD.A’B’C’D’ là hình hộp thì \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (Quy tắc hình hộp).

b) Hiệu của hai vecto

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \).

Phép lấy hiệu của hai vecto được gọi là phép trừ vecto.

Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu).

2. Tích của một số với một vecto trong không gian

Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau:

- Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0.

- Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\).

Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto.

3. Tích vô hướng của hai vecto trong không gian

a) Góc giữa hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\).

b) Tích vô hướng của hai vecto trong không gian

Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức

\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).

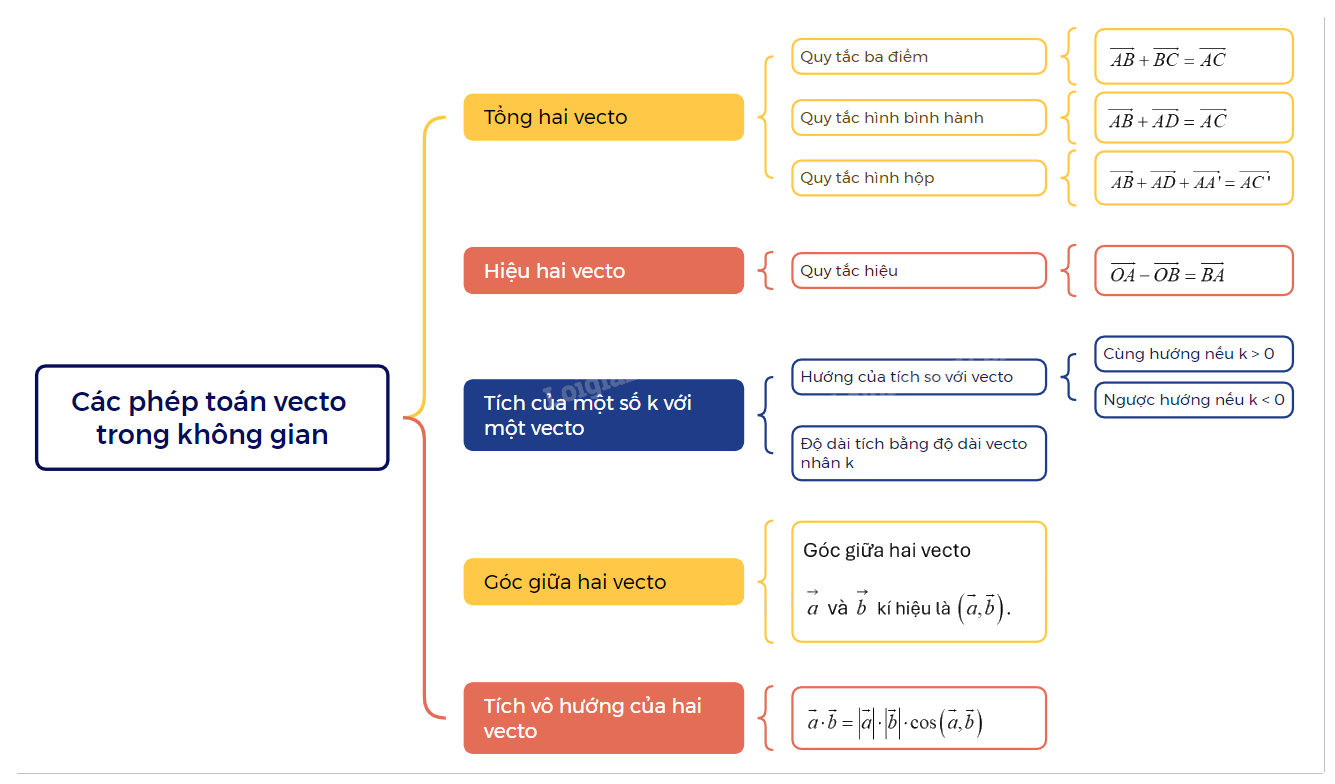
Lý thuyết Các phép toán vecto trong không gian Toán 12 Cùng khám phá 1

Lý Thuyết Các Phép Toán Vectơ Trong Không Gian Toán 12

Trong chương trình Toán 12, phần vectơ trong không gian đóng vai trò quan trọng, là nền tảng cho nhiều bài toán hình học và vật lý. Việc nắm vững lý thuyết và kỹ năng thực hành các phép toán vectơ là điều cần thiết để đạt kết quả tốt trong kỳ thi THPT Quốc gia.

1. Khái Niệm Cơ Bản Về Vectơ Trong Không Gian

Vectơ trong không gian là một đoạn thẳng có hướng, được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu là AB hoặc a. Một vectơ có thể được biểu diễn bằng tọa độ trong một hệ tọa độ vuông góc Oxyz: a = (x; y; z).

2. Các Phép Toán Vectơ Cơ Bản

Phép cộng vectơ:a + b = (x1 + x2; y1 + y2; z1 + z2)
Phép trừ vectơ:a - b = (x1 - x2; y1 - y2; z1 - z2)
Phép nhân vectơ với một số thực:k.a = (kx; ky; kz)

3. Tích Vô Hướng Của Hai Vectơ

Tích vô hướng của hai vectơ a và b, ký hiệu là a.b, được tính bằng:

a.b = x1x2 + y1y2 + z1z2

Ứng dụng của tích vô hướng:

Tính góc giữa hai vectơ: cos(α) = (a.b) / (|a||b|)
Kiểm tra tính vuông góc: a ⊥ b ⇔ a.b = 0

4. Tích Có Hướng Của Hai Vectơ

Tích có hướng của hai vectơ a và b, ký hiệu là a x b, là một vectơ vuông góc với cả hai vectơ a và b. Tích có hướng được tính bằng định thức:

a x b = (y1z2 - y2z1; z1x2 - z2x1; x1y2 - x2y1)

Ứng dụng của tích có hướng:

Tính diện tích hình bình hành tạo bởi hai vectơ: S = |a x b|
Tìm vectơ pháp tuyến của mặt phẳng: Vectơ tích có hướng của hai vectơ nằm trong mặt phẳng là vectơ pháp tuyến của mặt phẳng đó.

5. Bài Tập Vận Dụng

Để củng cố kiến thức, hãy cùng giải một số bài tập ví dụ:

Cho a = (1; 2; 3) và b = (4; 5; 6). Tính a + b, a - b và a.b.
Cho a = (1; 0; 0) và b = (0; 1; 0). Tính a x b.

6. Lời Khuyên Khi Học Lý Thuyết Vectơ

Nắm vững định nghĩa và tính chất của vectơ.
Thực hành nhiều bài tập để làm quen với các phép toán.
Sử dụng hình ảnh minh họa để hiểu rõ hơn về các khái niệm.
Kết hợp lý thuyết với các ứng dụng thực tế.

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết các phép toán vectơ trong không gian Toán 12. Chúc bạn học tập tốt và đạt kết quả cao trong kỳ thi!