Giải bài tập 1.5 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.5 Trang 9 Toán 12 Tập 1 - Cùng Khám Phá
Bài tập 1.5 trang 9 SGK Toán 12 tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số, một khái niệm nền tảng trong giải tích.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
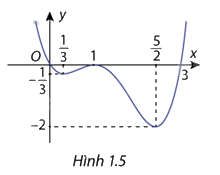
Cho hàm số \(y = f(x)\)liên tục trên đoạn \([0;3]\) thõa mãn \(f'\left( {\frac{1}{3}} \right) = f'(1) = f'\left( {\frac{5}{2}} \right) = 0\)và có đồ thị là đường cong như hình 1.5. Xác định các khoảng đơn điệu và tìm cực trị hàm số đã cho trên khoảng \((0;3)\)
Đề bài
Cho hàm số \(y = f(x)\)liên tục trên đoạn \([0;3]\) thõa mãn \(f'\left( {\frac{1}{3}} \right) = f'(1) = f'\left( {\frac{5}{2}} \right) = 0\)và có đồ thị là đường cong như hình 1.5. Xác định các khoảng đơn điệu và tìm cực trị hàm số đã cho trên khoảng \((0;3)\)
Phương pháp giải - Xem chi tiết
Từ những điều kiện bài cho lập bảng biến thiên rồi biện luận tính đơn điệu và cực trị hàm số
Lời giải chi tiết
Dựa vào dồ thị hàm số ta có:
Hàm số dồng biến trên khoảng \(\left( {\frac{1}{3};1} \right)\) và \(\left( {\frac{5}{2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {1;\frac{5}{2}} \right)\)
Từ đồ thị hàm số ta lại có bảng biến thiên là:
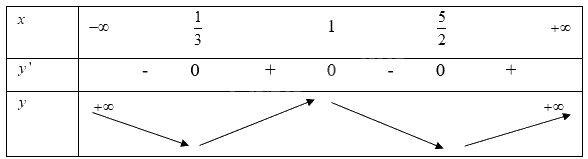
Từ bảng biến thiên ta có:
Hàm số đạt cực trị tại các điểm \(x = \frac{1}{3}\) , \(x = 1\) ,\(x = \frac{5}{2}\)
Giải Bài Tập 1.5 Trang 9 Toán 12 Tập 1: Hướng Dẫn Chi Tiết
Bài tập 1.5 trang 9 SGK Toán 12 tập 1 yêu cầu chúng ta tính giới hạn của hàm số. Để giải bài tập này, chúng ta cần nắm vững các quy tắc tính giới hạn, đặc biệt là giới hạn của các hàm số đơn giản và các phép toán trên giới hạn.
Nội dung bài tập 1.5 trang 9 SGK Toán 12 tập 1
Bài tập thường có dạng tính limx→a f(x), trong đó f(x) là một hàm số và a là một giá trị cụ thể.
Phương pháp giải bài tập 1.5 trang 9 SGK Toán 12 tập 1
- Xác định dạng của hàm số: Hàm số có thể là đa thức, phân thức, hàm căn thức, hàm lượng giác, hoặc một tổ hợp của chúng.
- Áp dụng các quy tắc tính giới hạn:
- Giới hạn của một tổng/hiệu bằng tổng/hiệu các giới hạn.
- Giới hạn của một tích bằng tích các giới hạn.
- Giới hạn của một thương bằng thương các giới hạn (với mẫu khác 0).
- Nếu f(x) là đa thức thì limx→a f(x) = f(a).
- Các giới hạn đặc biệt của hàm lượng giác (ví dụ: limx→0 sin(x)/x = 1).
- Biến đổi hàm số: Nếu cần thiết, hãy biến đổi hàm số để đưa về dạng có thể tính giới hạn được. Ví dụ, nhân tử và mẫu của phân thức với một biểu thức thích hợp để khử các yếu tố gây ra vô định.
- Tính giới hạn: Sau khi đã áp dụng các quy tắc và biến đổi hàm số, hãy tính giới hạn.
Ví dụ minh họa giải bài tập 1.5 trang 9 SGK Toán 12 tập 1
Giả sử bài tập yêu cầu tính limx→2 (x2 - 4) / (x - 2).
- Hàm số là phân thức.
- Ta có thể phân tích tử số thành (x - 2)(x + 2).
- Khi đó, limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2).
- Vậy, limx→2 (x + 2) = 2 + 2 = 4.
Lưu ý khi giải bài tập 1.5 trang 9 SGK Toán 12 tập 1
- Luôn kiểm tra xem có thể áp dụng trực tiếp các quy tắc tính giới hạn hay không.
- Nếu không, hãy cố gắng biến đổi hàm số để đưa về dạng đơn giản hơn.
- Chú ý đến các trường hợp vô định và sử dụng các phương pháp phù hợp để giải quyết chúng.
- Thực hành nhiều bài tập để nắm vững kiến thức và kỹ năng.
Tại sao nên chọn tusach.vn để giải bài tập Toán 12?
tusach.vn cung cấp:
- Lời giải chi tiết, dễ hiểu, được trình bày rõ ràng.
- Đội ngũ giáo viên giàu kinh nghiệm, chuyên môn cao.
- Cập nhật liên tục các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Hãy truy cập tusach.vn ngay hôm nay để giải quyết mọi khó khăn trong học tập Toán 12!