Giải bài tập 6.7 trang 101 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 6.7 Trang 101 SGK Toán 12 Tập 2
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 6.7 trang 101 SGK Toán 12 tập 2. Bài tập này thuộc chương trình học về Đạo Hàm, một trong những chủ đề quan trọng của Toán học lớp 12.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Bạn Nam tham gia một gian hàng trò chơi dân gian trong hội xuân của trường. Trò chơi có hai lượt chơi. Xác suất để Nam thắng ở lượt chơi thứ nhất là 0,6. Nếu Nam thắng ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,8. Ngược lại, nếu Nam thua ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,3. a) Vẽ sơ đồ hình cây mô tả các khả năng xảy ra và xác suất tương ứng khi Nam tham gia trò chơi này. b) Biết Nam đã thắng ở lượt chơi thứ hai, tính xác suất Nam th
Đề bài
Bạn Nam tham gia một gian hàng trò chơi dân gian trong hội xuân của trường. Trò chơi có hai lượt chơi. Xác suất để Nam thắng ở lượt chơi thứ nhất là 0,6. Nếu Nam thắng ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,8. Ngược lại, nếu Nam thua ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,3.
a) Vẽ sơ đồ hình cây mô tả các khả năng xảy ra và xác suất tương ứng khi Nam tham gia trò chơi này.
b) Biết Nam đã thắng ở lượt chơi thứ hai, tính xác suất Nam thắng ở lượt chơi thứ nhất.
Phương pháp giải - Xem chi tiết
a)
- Biểu diễn các khả năng thắng/thua của Nam trong hai lượt chơi.
- Xác suất tương ứng được tính từ dữ kiện bài toán.
b)
Tính xác suất Nam thắng lượt thứ nhất khi biết Nam thắng lượt thứ hai:
\(P(A|B) = \frac{{P(B|A) \cdot P(A)}}{{P(B)}}\)
trong đó:
- \(A\): Biến cố Nam thắng ở lượt thứ nhất.
- \(B\): Biến cố Nam thắng ở lượt thứ hai.
Sử dụng công thức tính xác suất toàn phần để tính \(P(B)\) (Nam thắng ở lượt thứ hai):
\(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A)\)
Lời giải chi tiết
a)
Gọi:
- \(A\): Biến cố Nam thắng ở lượt thứ nhất.
- \(B\): Biến cố Nam thắng ở lượt thứ hai.
Sơ đồ hình cây mô tả các khả năng và xác suất tương ứng như sau:
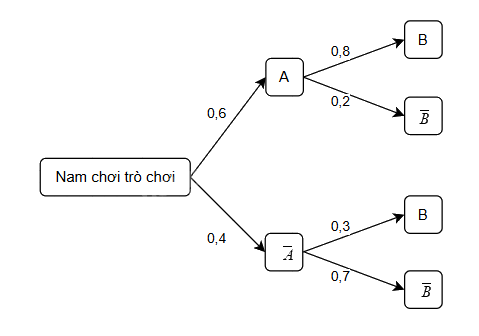
- \(P(A) = 0,6\), \(P(\bar A) = 0,4\).
- Nếu \(A\) (Nam thắng lượt thứ nhất): \(P(B|A) = 0,8\), \(P(\bar B|A) = 0,2\).
- Nếu \(\bar A\) (Nam thua lượt thứ nhất): \(P(B|\bar A) = 0,3\), \(P(\bar B|\bar A) = 0,7\).
b)
* Tính \(P(B)\) bằng công thức xác suất toàn phần:
\(P(B) = P(B|A) \cdot P(A) + P(B|\bar A) \cdot P(\bar A).\)
\(P(B) = (0,8 \cdot 0,6) + (0,3 \cdot 0,4) = 0,48 + 0,12 = 0,6.\)
* Tính \(P(A|B)\) bằng định lý Bayes:
\(P(A|B) = \frac{{P(B|A) \cdot P(A)}}{{P(B)}}.\)
\(P(A|B) = \frac{{0,8 \cdot 0,6}}{{0,6}} = 0,8.\)
Giải Bài Tập 6.7 Trang 101 SGK Toán 12 Tập 2: Phương Pháp Giải Chi Tiết
Bài tập 6.7 trang 101 SGK Toán 12 tập 2 yêu cầu chúng ta tìm đạo hàm của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm:
- Quy tắc đạo hàm của một tổng: (u + v)' = u' + v'
- Quy tắc đạo hàm của một tích: (uv)' = u'v + uv'
- Quy tắc đạo hàm của một thương: (u/v)' = (u'v - uv')/v2
- Quy tắc đạo hàm của hàm hợp: y' = u' * v' (với y = f(u) và u = g(x))
- Đạo hàm của các hàm số cơ bản: Ví dụ: (xn)' = nxn-1, (sin x)' = cos x, (cos x)' = -sin x, (ex)' = ex, (ln x)' = 1/x
Phân Tích Đề Bài và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ hàm số cần tìm đạo hàm và các quy tắc đạo hàm nào sẽ được áp dụng. Việc lập kế hoạch giải sẽ giúp chúng ta tiếp cận bài toán một cách có hệ thống và tránh sai sót.
Lời Giải Chi Tiết Bài Tập 6.7 Trang 101 SGK Toán 12 Tập 2
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm y'.)
Giải:
Áp dụng quy tắc đạo hàm của một tổng và quy tắc đạo hàm của lũy thừa, ta có:
y' = (x3)' - 3(x2)' + (2)'
y' = 3x2 - 3(2x) + 0
y' = 3x2 - 6x
Ví Dụ Minh Họa và Bài Tập Tương Tự
Để hiểu rõ hơn về cách giải bài tập đạo hàm, chúng ta hãy xem xét một ví dụ khác:
(Ví dụ: Cho hàm số y = sin(2x). Tìm y'.)
Giải:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
y' = cos(2x) * (2x)'
y' = cos(2x) * 2
y' = 2cos(2x)
Luyện Tập Thêm với Các Bài Tập Tương Tự
Để củng cố kiến thức và kỹ năng giải bài tập đạo hàm, các em có thể tự luyện tập với các bài tập tương tự sau:
- Tìm đạo hàm của hàm số y = 5x4 + 2x - 1
- Tìm đạo hàm của hàm số y = cos(x2)
- Tìm đạo hàm của hàm số y = e3x
Tổng Kết và Lời Khuyên
Việc nắm vững các quy tắc đạo hàm cơ bản và luyện tập thường xuyên là chìa khóa để giải quyết thành công các bài tập về đạo hàm. Hãy luôn đọc kỹ đề bài, lập kế hoạch giải và kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 6.7 trang 101 SGK Toán 12 tập 2 và tự tin hơn trong quá trình học tập. Chúc các em học tốt!
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của tổng | (u + v)' = u' + v' |
| Đạo hàm của tích | (uv)' = u'v + uv' |