Lý Thuyết Giá Trị Lớn Nhất, Nhỏ Nhất Hàm Số Toán 12

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12

Trong chương trình Toán 12, bài toán tìm giá trị lớn nhất (max) và giá trị nhỏ nhất (min) của hàm số là một chủ đề quan trọng, thường xuyên xuất hiện trong các kỳ thi.

Việc nắm vững lý thuyết và phương pháp giải bài tập liên quan đến chủ đề này không chỉ giúp học sinh hiểu sâu hơn về hàm số mà còn rèn luyện kỹ năng tư duy logic và giải quyết vấn đề.

1. Định nghĩa

1. Định nghĩa

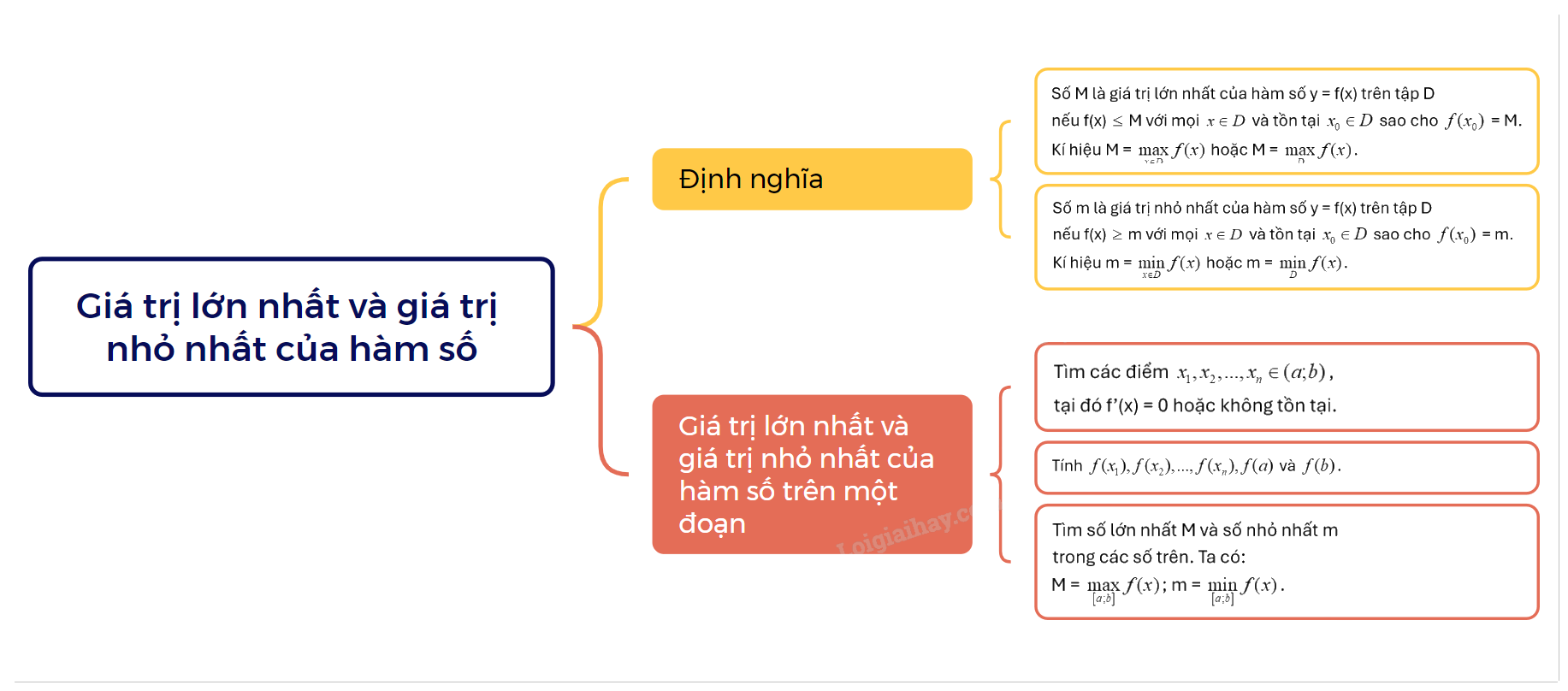
Cho hàm số y = f(x) xác định trên tập D.

+) Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) \( \le \) M với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = M. Kí hiệu M = \(\mathop {\max }\limits_{x \in D} f(x)\) hoặc M = \(\mathop {\max }\limits_D f(x)\).

+) Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) \( \ge \) m với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = m. Kí hiệu m = \(\mathop {\min }\limits_{x \in D} f(x)\) hoặc m = \(\mathop {\min }\limits_D f(x)\).

Ví dụ: Tìm GTLN, GTNN của hàm số \(y = f(x) = \sqrt {1 - {x^2}} \).

Tập xác định của hàm số là \(\left[ { - 1;1} \right]\).

Ta có:

\(f(x) = \sqrt {1 - {x^2}} \) \( \ge \) 0; dấu bằng xảy ra khi \(1 - {x^2} = 0\), tức x = -1 hoặc x = 1.

Do đó \(\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0\).

\(f(x) = \sqrt {1 - {x^2}} \) \( \le 1\); dấu bằng xảy ra khi \(1 - {x^2} = 1\), tức x = 0.

Do đó \(\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1\).

2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\):

Tìm các điểm \({x_1},{x_2},...,{x_n} \in (a;b)\), tại đó f’(x) = 0 hoặc không tồn tại.
Tính \(f({x_1}),f({x_2}),...,f({x_n}),f(a)\) và \(f(b)\).
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
M = \(\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)\); m = \(\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)\).

Ví dụ: Tìm GTLN và GTNN của hàm số \(y = {x^4} - 4{x^2} + 3\) trên đoạn \(\left[ {0;4} \right]\).

Ta có: \(y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 2 \) (vì \(x \in \left[ {0;4} \right]\)).

y(0) = 3; y(4) = 195; y(\(\sqrt 2 \)) = -1.

Do đó: \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195\); \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1\).

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá 1

Lý Thuyết Giá Trị Lớn Nhất và Giá Trị Nhỏ Nhất của Hàm Số Toán 12 - Tusach.vn

Chào mừng các bạn đến với bài viết tổng hợp lý thuyết và phương pháp giải bài tập về Giá trị lớn nhất và Giá trị nhỏ nhất của hàm số trong chương trình Toán 12. Bài viết này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm của Tusach.vn, với mục tiêu cung cấp cho các bạn một nguồn tài liệu học tập đầy đủ, dễ hiểu và hiệu quả.

1. Khái niệm cơ bản

Giá trị lớn nhất (max) của hàm số f(x) trên một khoảng K được gọi là giá trị M sao cho f(x) ≤ M với mọi x thuộc K, và tồn tại ít nhất một x₀ thuộc K sao cho f(x₀) = M.

Giá trị nhỏ nhất (min) của hàm số f(x) trên một khoảng K được gọi là giá trị m sao cho f(x) ≥ m với mọi x thuộc K, và tồn tại ít nhất một x₀ thuộc K sao cho f(x₀) = m.

2. Điều kiện để hàm số đạt giá trị lớn nhất, giá trị nhỏ nhất trên một khoảng đóng [a, b]

Nếu hàm số f(x) liên tục trên đoạn [a, b] thì:

f(x) đạt giá trị lớn nhất và giá trị nhỏ nhất trên [a, b].
Giá trị lớn nhất và giá trị nhỏ nhất có thể xảy ra tại các điểm sau:

Các điểm mà f'(x) = 0 (điểm dừng).
Các điểm mà f'(x) không tồn tại.
Các đầu mút của đoạn [a, b], tức là a và b.

3. Phương pháp giải bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất

Xác định tập xác định của hàm số.
Tính đạo hàm f'(x).
Tìm các điểm dừng (f'(x) = 0) và các điểm mà f'(x) không tồn tại.
Tính giá trị của hàm số tại các điểm dừng, điểm mà đạo hàm không tồn tại và các đầu mút của khoảng (nếu có).
So sánh các giá trị đã tính để tìm ra giá trị lớn nhất và giá trị nhỏ nhất.

4. Ví dụ minh họa

Ví dụ 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x³ - 3x² + 2 trên đoạn [-1, 3].

Giải:

f'(x) = 3x² - 6x
f'(x) = 0 ⇔ 3x² - 6x = 0 ⇔ x = 0 hoặc x = 2
f(-1) = 0
f(0) = 2
f(2) = -2
f(3) = 2

Vậy, giá trị lớn nhất của hàm số trên đoạn [-1, 3] là 2, đạt được tại x = 0 và x = 3. Giá trị nhỏ nhất của hàm số trên đoạn [-1, 3] là -2, đạt được tại x = 2.

5. Lưu ý quan trọng

Khi giải bài tập về giá trị lớn nhất và giá trị nhỏ nhất, cần chú ý:

Kiểm tra kỹ điều kiện của bài toán (khoảng xác định, tính liên tục của hàm số).
Tính đạo hàm chính xác.
Không bỏ sót các điểm mà đạo hàm bằng 0 hoặc không tồn tại.
So sánh tất cả các giá trị để tìm ra giá trị lớn nhất và giá trị nhỏ nhất.

6. Bài tập luyện tập

Để củng cố kiến thức, các bạn có thể tự giải các bài tập sau:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = 2x² - 4x + 1 trên đoạn [0, 2].
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x⁴ - 2x² + 3 trên khoảng [-2, 2].

Hy vọng bài viết này đã cung cấp cho các bạn những kiến thức hữu ích về lý thuyết Giá trị lớn nhất và Giá trị nhỏ nhất của hàm số Toán 12. Chúc các bạn học tập tốt và đạt kết quả cao trong các kỳ thi!

Truy cập tusach.vn để xem thêm nhiều tài liệu học tập Toán 12 hữu ích khác.