Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 2.25 trang 82 SGK Toán 12 tập 1 - Cùng khám phá
SGK Toán 12 - Cùng khám phá
Giải Toán 12 tập 1 - Cùng khám phá
Chương 2. Vecto và hệ tọa độ trong không gian
Bài tập cuối chương 2

Giải bài tập 2.25 trang 82 SGK Toán 12 tập 1 - Cùng khám phá

Giải Bài Tập 2.25 Trang 82 SGK Toán 12 Tập 1

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.25 trang 82 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.

Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3. a) Tìm tọa độ các đỉnh của hình hộp. b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\).

Đề bài

Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ O, các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz và AB = 1, AD = 2, AA’ = 3.

a) Tìm tọa độ các đỉnh của hình hộp.

b) Tìm điểm E trên đường thẳng DD’ sao cho \(B'E \bot A'C'\).

Phương pháp giải - Xem chi tiếtGiải bài tập 2.25 trang 82 SGK Toán 12 tập 1 - Cùng khám phá 1

a) Sử dụng thông tin về các cạnh của hình hộp để xác định tọa độ của các đỉnh.

b) Tìm vectơ chỉ phương của đường thẳng DD’ và B’E. Sử dụng điều kiện \(B'E \bot A'C'\) để thiết lập phương trình và giải tìm tọa độ của E.

Lời giải chi tiết

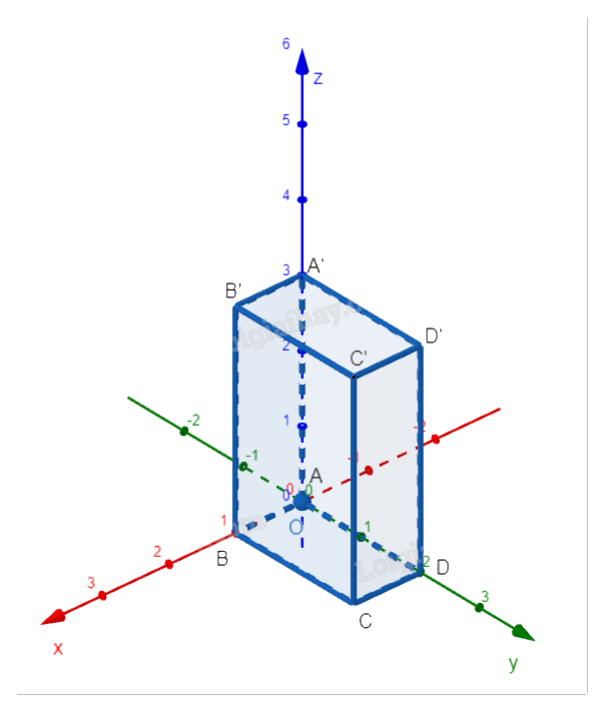
Giải bài tập 2.25 trang 82 SGK Toán 12 tập 1 - Cùng khám phá 2

a) Tọa độ các đỉnh của hình hộp chữ nhật là:

- A trùng với gốc tọa độ, tức A(0; 0; 0) .

- B thuộc tia Ox , nên B(1; 0; 0) (vì AB = 1 ).

- D thuộc tia Oy , nên D(0; 2; 0) (vì AD = 2 ).

- A’ thuộc tia Oz , nên A’(0; 0; 3) (vì AA’ = 3 ).

Các đỉnh còn lại của hình hộp chữ nhật:

- C đối với A qua BD , tọa độ là C(1; 2; 0) .

- B’ đối với A qua A’C , tọa độ là B’(1; 0; 3) .

- D’ đối với A qua A’D , tọa độ là D’(0; 2; 3) .

- C’ đối với A qua B’D , tọa độ là C’(1; 2; 3) .

b) Tọa độ của điểm E trên đường thẳng DD’ :

- Đường thẳng DD’ có phương trình dạng:

\(x = 0,\quad y = 2,\quad z = t{\rm{.}}\) với t là tham số.

Tọa độ của E là E(0; 2; t) . Để \(B'E \bot A'C\), cần:

\(\overrightarrow {B'E} \cdot \overrightarrow {A'C} = 0\)

Tính các vectơ:

\(\overrightarrow {B'E} = (0 - 1;2 - 0;t - 3) = ( - 1;2;t - 3)\)

\(\overrightarrow {A'C} = (1 - 0;2 - 0;0 - 3) = (1;2; - 3)\)

Điều kiện vuông góc:

\(\overrightarrow {BE} \cdot \overrightarrow {A'C} = ( - 1) \times 1 + 2 \times 2 + (t - 3) \times ( - 3) = - 1 + 4 - 3t + 9 = 0\)

Giải phương trình này:

\( - 1 + 4 - 3t + 9 = 0\quad \Rightarrow \quad 12 = 3t\quad \Rightarrow \quad t = 4\)

Vậy tọa độ của E là E(0; 2; 4) .

Giải Bài Tập 2.25 Trang 82 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 2.25 trang 82 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

Đề Bài Bài Tập 2.25

Cho hàm số y = f(x) = x3 - 3x2 + 2. Hãy:

  1. Xác định các điểm cực trị của hàm số.
  2. Tìm khoảng đồng biến, nghịch biến của hàm số.

Lời Giải Chi Tiết

Bước 1: Tìm tập xác định của hàm số

Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.

Bước 2: Tính đạo hàm cấp nhất

f'(x) = 3x2 - 6x

Bước 3: Tìm các điểm cực trị

Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:

3x2 - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2.

Bước 4: Xác định loại điểm cực trị

Ta xét dấu của f'(x) trên các khoảng:

  • Khoảng (-∞; 0): Chọn x = -1, f'(-1) = 3(-1)2 - 6(-1) = 9 > 0, hàm số đồng biến.
  • Khoảng (0; 2): Chọn x = 1, f'(1) = 3(1)2 - 6(1) = -3 < 0, hàm số nghịch biến.
  • Khoảng (2; +∞): Chọn x = 3, f'(3) = 3(3)2 - 6(3) = 9 > 0, hàm số đồng biến.

Vậy:

  • Tại x = 0, hàm số đạt cực đại và giá trị cực đại là f(0) = 2.
  • Tại x = 2, hàm số đạt cực tiểu và giá trị cực tiểu là f(2) = 23 - 3(2)2 + 2 = -2.

Bước 5: Tìm khoảng đồng biến, nghịch biến

Dựa vào bảng xét dấu của f'(x), ta có:

  • Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
  • Hàm số nghịch biến trên khoảng (0; 2).

Kết Luận

Vậy, bài tập 2.25 trang 82 SGK Toán 12 tập 1 đã được giải quyết như sau:

  • Điểm cực đại: (0; 2)
  • Điểm cực tiểu: (2; -2)
  • Khoảng đồng biến: (-∞; 0) và (2; +∞)
  • Khoảng nghịch biến: (0; 2)

Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập khảo sát hàm số bằng đạo hàm. Chúc các em học tập tốt!

Mở Rộng Kiến Thức

Để nắm vững hơn về chủ đề này, các em có thể tham khảo thêm các bài tập tương tự trong SGK và sách bài tập Toán 12 tập 1. Ngoài ra, các em cũng có thể tìm hiểu thêm về các ứng dụng khác của đạo hàm trong thực tế.

Tusach.vn luôn cập nhật những lời giải bài tập mới nhất và chất lượng nhất. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN