Đề bài
Cho tứ diện ABCD. Hai điểm M và N theo thứ tự là trung điểm của BC và AD. Cho biết AB = 10, CD = 6, MN = 7.
a) Chứng minh rằng \(\overrightarrow {NM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\).
b) Từ kết quả câu a, hãy tính \(\overrightarrow {AB} .\overrightarrow {DC} \).
c) Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right)\).
Phương pháp giải - Xem chi tiết
a) Để chứng minh \(\overrightarrow {NM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\), ta cần sử dụng tính chất trung điểm và phép cộng vectơ.
b) Sử dụng kết quả từ phần a) để tính tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {DC} \). Áp dụng tính chất “Bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó”.
c) Sử dụng tích vô hướng để tìm góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \).
\(\cos \theta = \frac{{\overrightarrow {AB} \cdot \overrightarrow {DC} }}{{|\overrightarrow {AB} | \cdot |\overrightarrow {DC} |}}\)
Lời giải chi tiết
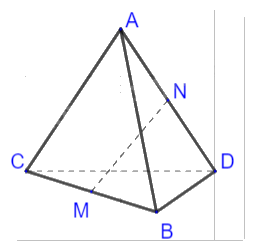
a) Chứng minh \(\overrightarrow {NM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\):
- Vì \(M\) là trung điểm của BC, nên \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BC} \).
- Vì \(N\) là trung điểm của AD, nên \(\overrightarrow {AN} = \frac{1}{2}\overrightarrow {AD} \).
- Vectơ \(\overrightarrow {NM} \) có thể được viết là: \(\overrightarrow {NM} = \overrightarrow {NB} + \overrightarrow {BM} \).
Với: \(\overrightarrow {NB} = \overrightarrow {NA} + \overrightarrow {AB} = \frac{1}{2}\overrightarrow {DA} + \overrightarrow {AB} \)
Và: \(\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BC} = \frac{1}{2}\left( {\overrightarrow {BD} + \overrightarrow {DC} } \right)\).
Suy ra: \(\overrightarrow {NM} = \frac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {BD} } \right) + \overrightarrow {AB} + \frac{1}{2}\overrightarrow {DC} = \frac{1}{2}\overrightarrow {BA} + \overrightarrow {AB} + \frac{1}{2}\overrightarrow {DC} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} )\).
b) Từ kết quả câu a, tính \(\overrightarrow {AB} \cdot \overrightarrow {DC} \):
- Từ câu a, ta có:
\(\overrightarrow {NM} \cdot \overrightarrow {NM} = \frac{1}{4}(\overrightarrow {AB} + \overrightarrow {DC} ) \cdot (\overrightarrow {AB} + \overrightarrow {DC} )\).
Biểu thức này mở rộng thành:
\(\frac{1}{4}(\overrightarrow {AB} \cdot \overrightarrow {AB} + 2\overrightarrow {AB} \cdot \overrightarrow {DC} + \overrightarrow {DC} \cdot \overrightarrow {DC} )\).
Biết rằng \(\overrightarrow {NM} \cdot \overrightarrow {NM} = M{N^2} = 49\), \(AB = 10\), \(DC = 6\), ta suy ra:
\(49 = \frac{1}{4}(100 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} + 36)\).
\(49 = \frac{1}{4}(136 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} )\).
\(196 = 136 + 2\overrightarrow {AB} \cdot \overrightarrow {DC} \).
\(\overrightarrow {AB} \cdot \overrightarrow {DC} = 30\).
c) Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right)\):
- Góc giữa hai vectơ được tính bởi:
\(\cos \theta = \frac{{\overrightarrow {AB} \cdot \overrightarrow {DC} }}{{|\overrightarrow {AB} | \cdot |\overrightarrow {DC} |}}\).
\(\cos \theta = \frac{{30}}{{10 \cdot 6}} = \frac{1}{2}\).
Suy ra \(\theta = {60^\circ }\).
