Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2

Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 - Cùng khám phá

Bài tập 4.38 trang 38 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4.38 trang 38 SGK Toán 12 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

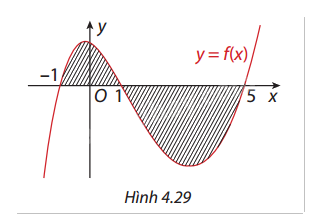
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f(x),y = 0,x = - 1\) và \(x = 5\) (Hình 4.29). Mệnh đề nào sau đây dúng?

Đề bài

Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 - Cùng khám phá 1

A. \(S = - \int_1^1 f (x)dx - \int_1^5 f (x)dx\)

B. \(S = \int_1^1 f (x)dx + \int_1^5 f (x)dx\)

C. \(S = \int_1^1 f (x)dx\quad \int_1^5 f (x)dx\)

D. \(S = - \int_{ - 1}^1 f (x)dx + \int_1^5 f (x)dx\)

Phương pháp giải - Xem chi tiết Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 - Cùng khám phá 2

Diện tích hình phẳng được xác định bằng tích phân của giá trị tuyệt đối của hàm số trên đoạn đã cho. Để tính diện tích, cần xem xét khoảng nào hàm số nằm phía dưới trục hoành và khoảng nào nằm phía trên trục hoành.

Lời giải chi tiết

Xét hình phẳng trong hình vẽ, hàm \(f(x)\) có phần nằm trên trục hoành (dương) từ \(x = - 1\) đến \(x = 1\), và phần nằm dưới trục hoành (âm) từ \(x = 1\) đến \(x = 5\).

- Với khoảng \(x = - 1\) dếdn \(x = 1\), \(f(x) > 0\)nên diện tích sẽ là \(\int_{ - 1}^1 f (x)dx\).

- Với khoảng \(x = 1\) đến \(x = 5\), \(f(x) < 0\) nên diện tích sẽ là \( - \int_1^5 f (x)dx\).

Tổng diện tích là:

\(S = \int_{ - 1}^1 f (x)dx - \int_1^5 f (x)dx\)

Chọn C.

Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2: Đạo hàm và ứng dụng

Bài tập 4.38 trang 38 SGK Toán 12 tập 2 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Đây là một phần kiến thức trọng tâm, thường xuyên xuất hiện trong các đề thi THPT Quốc gia. Việc nắm vững phương pháp giải các bài tập liên quan đến đạo hàm là vô cùng quan trọng để đạt kết quả cao trong môn Toán.

Đề bài bài tập 4.38 trang 38 SGK Toán 12 tập 2

(Đề bài cụ thể của bài tập 4.38 sẽ được chèn vào đây. Ví dụ: Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)(x+2). Tìm các điểm cực trị của hàm số.)

Phương pháp giải bài tập về đạo hàm

Để giải các bài tập về đạo hàm, chúng ta cần nắm vững các bước sau:

Tìm tập xác định của hàm số.
Tính đạo hàm f'(x).
Tìm các điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghiệm.
Xác định loại điểm cực trị: Sử dụng dấu của f'(x) khi x đi qua các điểm nghiệm để xác định điểm cực đại, cực tiểu.
Kết luận.

Lời giải chi tiết bài tập 4.38 trang 38 SGK Toán 12 tập 2

(Lời giải chi tiết của bài tập 4.38 sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và kết luận.)

Ví dụ minh họa và bài tập tương tự

Để hiểu rõ hơn về phương pháp giải, chúng ta cùng xem xét một số ví dụ minh họa và bài tập tương tự:

Ví dụ 1:(Đề bài và lời giải ví dụ 1)
Ví dụ 2:(Đề bài và lời giải ví dụ 2)

Lưu ý khi giải bài tập về đạo hàm

Khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:

Kiểm tra kỹ tập xác định của hàm số.
Tính đạo hàm chính xác.
Sử dụng dấu của đạo hàm một cách cẩn thận để xác định loại điểm cực trị.
Kiểm tra lại kết quả.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một website cung cấp tài liệu học tập Toán 12 uy tín, chất lượng. Chúng tôi cung cấp đầy đủ các bài giải SGK, bài tập trắc nghiệm, đề thi thử và các tài liệu tham khảo khác. Hãy truy cập Tusach.vn để học tập và ôn luyện Toán 12 hiệu quả!

Hy vọng với lời giải chi tiết và phương pháp giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 này, các em học sinh sẽ hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm. Chúc các em học tập tốt!