Giải bài tập 1.34 trang 46 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.34 Trang 46 Toán 12 Tập 1
Bài tập 1.34 trang 46 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này thường liên quan đến việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
Cho hàm số \(y = - {x^3} + 3x + 1\). Khảo sát sự biến thiên, vẽ đồ thị và chỉ ra tâm đối xứng của đồ thị hàm số đã cho.
Đề bài
Cho hàm số \(y = - {x^3} + 3x + 1\). Khảo sát sự biến thiên, vẽ đồ thị và chỉ ra tâm đối xứng của đồ thị hàm số đã cho.
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số
- Xét sự biến thiên của hàm số
- Vẽ đồ thị.
- Tính đạo hàm cấp hai và tìm điểm uốn của đồ thị hàm số.
Lời giải chi tiết
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3x + 1} \right) = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3x + 1} \right) = \infty \)
Ta có:
\({y^\prime } = - 3{x^2} + 3\)
\({y^\prime } = 0 \leftrightarrow - 3{x^2} + 3 = 0 \leftrightarrow x = \pm 1\)
Bảng biến thiên:
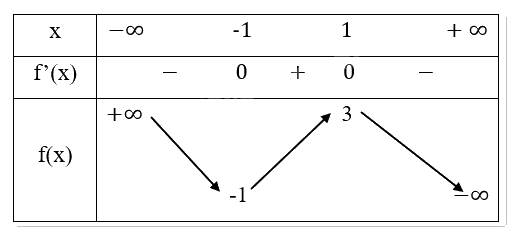
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-1) và (1,∞), đồng biến trên khoảng (-1,1).
Cực trị: Hàm số đạt cực tiểu tại \(x = - 1,{y_{CT}} = - 1\)
Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = 3\)
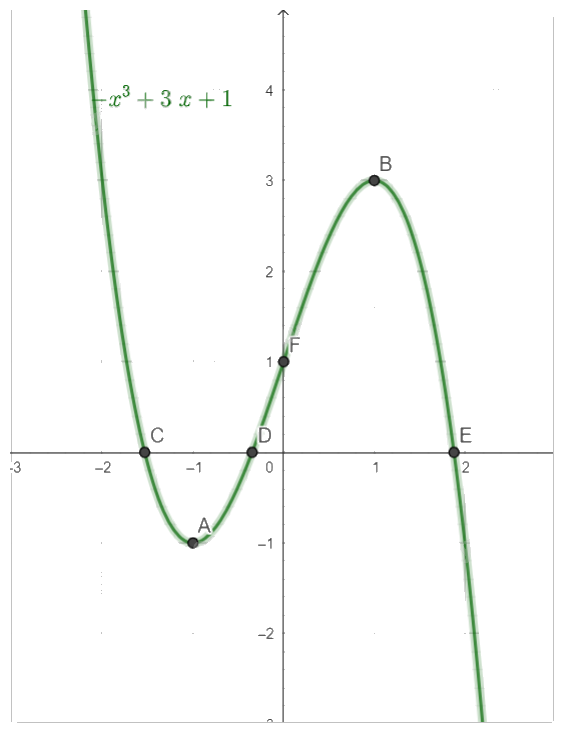
- Vẽ đồ thị:
Giao điểm với trục Oy là (0,1).
Giao điểm với trục Ox là (-1,53;0), (-0,53;0) và (1,88;0).
- Tính đạo hàm bậc hai: \(f''(x) = - 6x\)
- Giải phương trình \(f''(x) = 0\): \( - 6x = 0 \Leftrightarrow x = 0\)
\(x = 0 \to f(0) = 1\)
Vậy (0,1) là tâm đối xứng của đồ thị hàm số đã cho.
Giải Bài Tập 1.34 Trang 46 SGK Toán 12 Tập 1: Hướng Dẫn Chi Tiết
Bài tập 1.34 trang 46 SGK Toán 12 tập 1 thường xoay quanh việc tìm đạo hàm của hàm số và ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì và cách tính đạo hàm.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, đạo hàm của hàm hợp.
- Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit.
Phân Tích Đề Bài và Lập Kế Hoạch Giải
Trước khi bắt tay vào giải bài tập, điều quan trọng là phải đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và lập kế hoạch giải cụ thể. Điều này giúp bạn tránh được những sai sót không đáng có và tiết kiệm thời gian.
Lời Giải Chi Tiết Bài Tập 1.34 Trang 46
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
- Bước 1: Tính đạo hàm cấp một y'
- Bước 2: Tìm các điểm làm đạo hàm cấp một bằng 0
- Bước 3: Lập bảng biến thiên
- Bước 4: Kết luận
y' = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Mở Rộng và Bài Tập Tương Tự
Để củng cố kiến thức về đạo hàm và ứng dụng đạo hàm, bạn có thể tự giải thêm các bài tập tương tự. Hãy chú ý đến việc phân tích đề bài, lập kế hoạch giải và kiểm tra lại kết quả sau khi giải xong.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu học tập khác như sách giáo khoa, sách bài tập, các trang web học trực tuyến để nâng cao kiến thức và kỹ năng giải toán.
Tusach.vn – Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Chúng tôi cung cấp đầy đủ các tài liệu học tập, lời giải bài tập chi tiết và các bài giảng chất lượng cao. Hãy truy cập Tusach.vn để khám phá thêm nhiều điều thú vị và hữu ích!