Giải Bài Tập 1.17 Trang 22 SGK Toán 12 Tập 1

Giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.17 trang 22 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về giới hạn của hàm số, một trong những kiến thức nền tảng quan trọng của môn Toán 12.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và đầy đủ nhất. Hãy cùng chúng tôi khám phá cách giải bài tập này nhé!

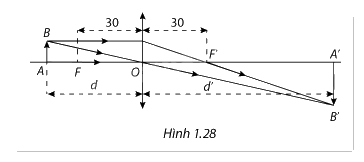
Một thấu kính hội tụ có tiêu cự f=30cm như hình 1.28. Trong vật lý, ta biết rằng nếu đặt vật thật AB cách quang tâm O của thấu kính một khoảng d(cm) lơn hơn 30cm thì được ảnh thật A’B’ cách quang tâm của thấu kính một khoảng d’(cm). Ngược lại, nếu 0<d<30 thì ta có ảnh ảo. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\). a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d. b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các

Đề bài

a) Từ công thức thấu kính, tìm biểu thức xác định d’ theo d.

b) Xem biểu thức của d’ ở câu a là một hàm số theo d, kí hiệu là h(d). Tìm các đường tiệm cận của h(d).

Giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 - Cùng khám phá 2

Từ công thức \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}}\) rút ra d’.

Tìm \(h\left( d \right)\;\), \(h\left( d \right)\;\).

Lời giải chi tiết

a) Ta có: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{{\rm{1}}}{{\rm{f}}} = \frac{1}{{30}}\)

\( \Rightarrow \frac{1}{{d'}} = \frac{{\rm{1}}}{{30}} - \frac{1}{d} = \frac{{d - 30}}{{30d}}\)

\( \Rightarrow d' = \frac{{30d}}{{d - 30}}\)

b) Ta có \(h(d) = \frac{{30d}}{{d - 30}}\)

c) \(\mathop {\lim }\limits_{d \to + \infty } h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to + \infty } \frac{{30}}{{1 - \frac{3}{d}}} = 30\;\)

Suy ra y = 30 là đường tiệm cận ngang của hàm số.

\(\mathop {\lim }\limits_{d \to {{30}^ + }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ + }} \frac{{30d}}{{d - 30}} = + \infty \;,\mathop {\lim }\limits_{d \to {{30}^ - }} h\left( d \right)\;\; = \mathop {\lim }\limits_{d \to {{30}^ - }} \frac{{30d}}{{d - 30}} = - \infty \;\)

Suy ra x = 30 là đường tiệm cận đứng của h(d).

Giải Bài Tập 1.17 Trang 22 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 1.17 trang 22 SGK Toán 12 tập 1 yêu cầu chúng ta tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, đặc biệt là các giới hạn cơ bản và các quy tắc tính giới hạn.

Đề Bài Bài Tập 1.17

Đề bài thường có dạng tính lim (f(x)) khi x -> a, trong đó f(x) là một hàm số và a là một số thực hoặc vô cực.

Phương Pháp Giải Bài Tập Giới Hạn

Kiểm tra dạng vô định: Nếu khi thay x = a vào hàm số f(x) ta được một trong các dạng 0/0, ∞/∞, ∞ - ∞, 0 * ∞, thì ta cần biến đổi hàm số để khử dạng vô định.
Sử dụng các quy tắc tính giới hạn:
- Giới hạn của một tổng/hiệu bằng tổng/hiệu các giới hạn.
- Giới hạn của một tích bằng tích các giới hạn.
- Giới hạn của một thương bằng thương các giới hạn (với mẫu khác 0).
Sử dụng các giới hạn cơ bản: Ví dụ: lim (1/x) khi x -> ∞ = 0, lim (x^n) khi x -> ∞ = ∞ (n > 0).
Phân tích thành nhân tử: Đôi khi, việc phân tích thành nhân tử có thể giúp chúng ta khử dạng vô định.
Sử dụng định nghĩa giới hạn: Trong một số trường hợp, chúng ta cần sử dụng định nghĩa giới hạn để chứng minh sự tồn tại của giới hạn.

Ví dụ Giải Bài Tập 1.17 (Giả định một dạng bài tập cụ thể)

Ví dụ: Tính lim ( (x^2 - 1) / (x - 1) ) khi x -> 1.

Giải:

Khi thay x = 1 vào hàm số, ta được (1^2 - 1) / (1 - 1) = 0/0, là dạng vô định. Ta có thể phân tích thành nhân tử:

(x^2 - 1) / (x - 1) = (x - 1)(x + 1) / (x - 1) = x + 1 (với x ≠ 1)

Vậy, lim ( (x^2 - 1) / (x - 1) ) khi x -> 1 = lim (x + 1) khi x -> 1 = 1 + 1 = 2.

Lưu Ý Quan Trọng

Luôn kiểm tra kỹ điều kiện xác định của hàm số.
Sử dụng các quy tắc tính giới hạn một cách cẩn thận.
Thực hành nhiều bài tập để nắm vững phương pháp giải.

Tusach.vn – Nơi Đồng Hành Cùng Bạn Học Toán 12

Tusach.vn không chỉ cung cấp lời giải chi tiết cho bài tập 1.17 trang 22 SGK Toán 12 tập 1 mà còn có rất nhiều tài liệu học tập hữu ích khác, bao gồm lý thuyết, bài tập trắc nghiệm, và các bài giảng video. Hãy truy cập Tusach.vn ngay hôm nay để nâng cao kiến thức và đạt kết quả tốt nhất trong môn Toán 12!

Bảng Tổng Hợp Các Giới Hạn Cơ Bản

Giới hạn	Kết quả
lim (1/x) khi x -> ∞	0
lim (1/x) khi x -> 0+	+∞
lim (x^n) khi x -> ∞ (n > 0)	+∞