Lý thuyết Lý thuyết Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12 Cùng khám phá
Tổng quan nội dung
Lý thuyết Phương sai và Độ lệch chuẩn trong Toán 12
Bài viết này cung cấp lý thuyết đầy đủ về Phương sai và Độ lệch chuẩn của mẫu số liệu ghép nhóm, một chủ đề quan trọng trong chương trình Toán 12. Chúng ta sẽ cùng nhau tìm hiểu các khái niệm, công thức tính toán và cách áp dụng vào giải bài tập.
Tusach.vn hy vọng sẽ giúp bạn nắm vững kiến thức này một cách nhanh chóng và hiệu quả.
Phương sai và độ lệch chuẩn
Phương sai và độ lệch chuẩn
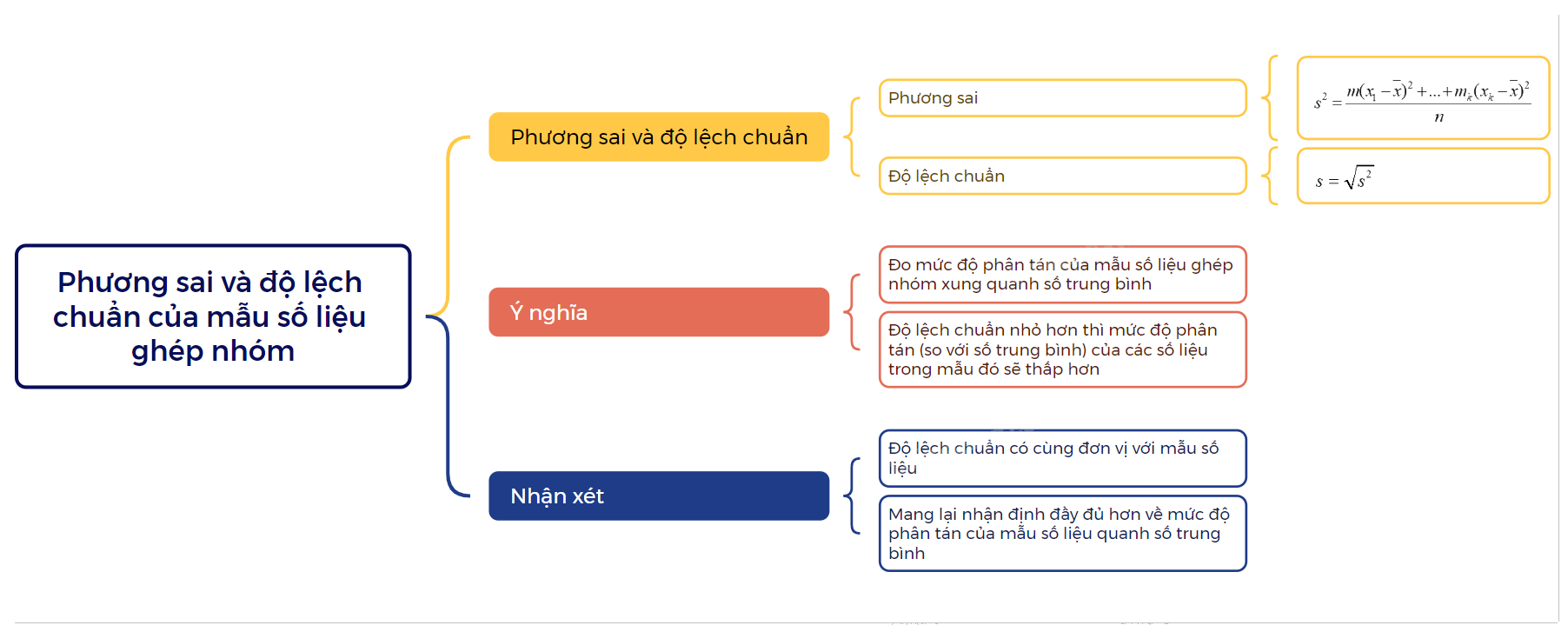
- Phương sai của mẫu số liệu ghép nhóm, kí hiệu là s2 , là một số được tính theo công thức sau: \({s^2} = \frac{{m{{({x_1} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\) trong đó, \(n = {m_1} + ... + {m_k}\); \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) với I = 1,2,…,k là giá trị đại diện cho nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) và \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm. - Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \). |
Ý nghĩa
- Phương sai (độ lệch chuẩn) của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó.
- Khi hai mẫu số liệu ghép nhóm có cùng đơn vị và có số trung bình bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình) của các số liệu trong mẫu đó sẽ thấp hơn.
Nhận xét
- Độ lệch chuẩn có cùng đơn vị với mẫu số liệu.
- Khác với khoảng biến thiên và khoảng tứ phân vị, phương sai (độ lệch chuẩn) đã xem xét tất cả các giá trị của mẫu số liệu nên có thể mang lại một nhận định đầy đủ hơn về mức độ phân tán của mẫu số liệu quanh số trung bình.
Lý thuyết Phương sai và Độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12
Phương sai và độ lệch chuẩn là hai đại lượng thống kê quan trọng, dùng để đo lường mức độ phân tán của một tập dữ liệu. Trong chương trình Toán 12, chúng ta xét đến phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm, một dạng dữ liệu thường gặp trong thực tế.
1. Khái niệm về Mẫu số liệu ghép nhóm
Mẫu số liệu ghép nhóm là một bảng tần số, trong đó các giá trị của biến ngẫu nhiên được chia thành các khoảng (nhóm) và mỗi khoảng được gán một tần số (số lần xuất hiện của các giá trị trong khoảng đó).
2. Công thức tính Phương sai của mẫu số liệu ghép nhóm
Phương sai (ký hiệu là s2) của mẫu số liệu ghép nhóm được tính theo công thức:
s2 = ∑i=1k fi(xi - x̄)2 / (n - 1)
Trong đó:
- fi là tần số của nhóm thứ i
- xi là trung điểm của nhóm thứ i
- x̄ là trung bình cộng của mẫu số liệu ghép nhóm (x̄ = ∑i=1k fixi / n)
- n là tổng số các giá trị trong mẫu (n = ∑i=1k fi)
3. Công thức tính Độ lệch chuẩn của mẫu số liệu ghép nhóm
Độ lệch chuẩn (ký hiệu là s) của mẫu số liệu ghép nhóm là căn bậc hai của phương sai:
s = √s2
4. Ý nghĩa của Phương sai và Độ lệch chuẩn
Phương sai và độ lệch chuẩn cho biết mức độ phân tán của dữ liệu xung quanh giá trị trung bình. Phương sai càng lớn, độ lệch chuẩn càng lớn, dữ liệu càng phân tán rộng. Ngược lại, phương sai và độ lệch chuẩn càng nhỏ, dữ liệu càng tập trung gần giá trị trung bình.
5. Ví dụ minh họa
Giả sử ta có bảng tần số sau:
| Khoảng | Tần số (fi) |
|---|---|
| [10, 20) | 5 |
| [20, 30) | 8 |
| [30, 40) | 7 |
| Tổng | 20 |
Trung điểm của các khoảng lần lượt là 15, 25, 35. Trung bình cộng của mẫu số liệu ghép nhóm là:
x̄ = (5*15 + 8*25 + 7*35) / 20 = 27.5
Phương sai của mẫu số liệu ghép nhóm là:
s2 = [5*(15-27.5)2 + 8*(25-27.5)2 + 7*(35-27.5)2] / (20-1) = 73.33
Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
s = √73.33 ≈ 8.56
6. Ứng dụng của Phương sai và Độ lệch chuẩn
Phương sai và độ lệch chuẩn được ứng dụng rộng rãi trong nhiều lĩnh vực như:
- Thống kê học: Đánh giá mức độ biến động của dữ liệu.
- Kinh tế: Đo lường rủi ro trong đầu tư.
- Khoa học: Phân tích kết quả thí nghiệm.
- Kỹ thuật: Kiểm soát chất lượng sản phẩm.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Phương sai và Độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức này nhé!
Truy cập tusach.vn để xem thêm nhiều tài liệu học tập Toán 12 hữu ích khác.