Giải Bài Tập 2.14 Trang 73 SGK Toán 12 Tập 1

Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.14 trang 73 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và đầy đủ nhất.

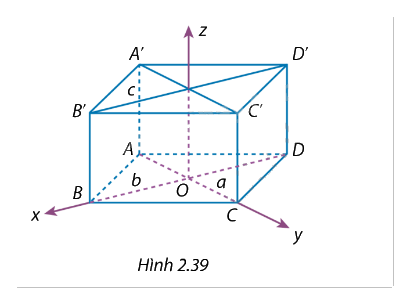
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).

Đề bài

a) Toạ độ các đỉnh của hình hộp;

b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).

Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá 2

- Sử dụng gốc tọa độ tại giao điểm của hai đường chéo hình thoi, xác định tọa độ các đỉnh đáy dựa vào chiều dài các đường chéo.

- Dùng công thức \(\overrightarrow {XY} = ({x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1})\) để tìm tọa độ vectơ \(\overrightarrow {BD'} \).

Lời giải chi tiết

a) Xác định tọa độ các đỉnh của hình hộp.

\(B\left( {\frac{b}{2},0,0} \right),{\rm{ }}A\left( {0,\frac{{ - a}}{2},0} \right),C\left( {0,\frac{a}{2},0} \right){\rm{, }}D\left( {\frac{{ - b}}{2},0,0} \right)\)

Tọa độ của các đỉnh A', B', C', D' lần lượt là:

\(B'\left( {\frac{b}{2},0,c} \right),{\rm{ }}A'\left( {0,\frac{{ - a}}{2},c} \right),C'\left( {0,\frac{a}{2},c} \right){\rm{, }}D'\left( {\frac{{ - b}}{2},0,c} \right)\)

b) Tọa độ vectơ \(\overrightarrow {BD'} :\)

\(\overrightarrow {BD'} = D' - B = ( - \frac{b}{2},0,c) - (\frac{b}{2},0,0) = ( - b,0,c)\)

Giải Bài Tập 2.14 Trang 73 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu

Bài tập 2.14 trang 73 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cực trị và cách xác định khoảng đồng biến, nghịch biến của hàm số.

Đề Bài Bài Tập 2.14

Cho hàm số y = f(x) = x³ - 3x² + 2. Hãy:

Xác định tập xác định của hàm số.
Tính đạo hàm f'(x).
Tìm các điểm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Vẽ đồ thị của hàm số.

Lời Giải Chi Tiết

1. Tập xác định:

Hàm số y = x³ - 3x² + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.

2. Tính đạo hàm:

f'(x) = 3x² - 6x

3. Tìm các điểm cực trị:

Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2.

Ta xét dấu của f'(x) trên các khoảng:

Khoảng (-∞; 0): f'(x) > 0, hàm số đồng biến.
Khoảng (0; 2): f'(x) < 0, hàm số nghịch biến.
Khoảng (2; +∞): f'(x) > 0, hàm số đồng biến.

Vậy, hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

f(0) = 2, điểm cực đại là (0; 2).

f(2) = 2³ - 3(2²) + 2 = 8 - 12 + 2 = -2, điểm cực tiểu là (2; -2).

4. Khảo sát sự biến thiên:

Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).

Hàm số nghịch biến trên khoảng (0; 2).

5. Vẽ đồ thị:

Dựa vào các thông tin đã tìm được, ta có thể vẽ đồ thị của hàm số y = x³ - 3x² + 2. Đồ thị sẽ đi qua các điểm cực trị (0; 2) và (2; -2), đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2).

Lưu Ý Quan Trọng

Khi giải các bài tập về khảo sát hàm số, điều quan trọng là phải nắm vững các bước thực hiện và áp dụng đúng các công thức, định lý. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán của mình.

Tusach.vn – Đồng Hành Cùng Bạn Học Toán 12

Tusach.vn luôn cập nhật những lời giải bài tập Toán 12 mới nhất và chính xác nhất. Hãy truy cập website của chúng tôi để tìm hiểu thêm và nhận được sự hỗ trợ tốt nhất trong quá trình học tập.

Chúc các em học tập tốt!