Giải bài tập 3.12 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 3.12 Trang 104 Toán 12 Tập 1
Bài tập 3.12 trang 104 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
Hàm lượng protein (trong 100g) của một số loại thực phẩm được cho trong bảng sau:
Đề bài
Hàm lượng protein (trong 100g) của một số loại thực phẩm được cho trong bảng sau:

a) Tìm khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu (làm tròn kết quả đến hàng phần trăm).
b) Nêu ý nghĩa của các kết quả tìm được.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức sau:
- Khoảng biến thiên là sự chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong tập dữ liệu.
- Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là:\({\Delta _Q} = {Q_3} - {Q_1}\) với công thức tính tứ phân vị là:
\({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
- Công thức tính trung bình là:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
- Công thức tính phương sai:
\({S^2} = \frac{1}{N}\sum\limits_{i = 1}^k {{n_i}({c_i}} - \overline x {)^2}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {{S^2}} \)
b)
Khoảng biến thiên: Cho biết độ phân tán tổng thể của dữ liệu, tức là khoảng cách giữa giá trị nhỏ nhất và giá trị lớn nhất trong mẫu.
Khoảng tứ phân vị: Phản ánh sự phân tán của dữ liệu ở phần trung tâm, loại bỏ ảnh hưởng của các giá trị cực đoan.
Độ lệch chuẩn: Cung cấp thông tin về mức độ dao động của các giá trị trong mẫu so với giá trị trung bình. Độ lệch chuẩn càng nhỏ, dữ liệu càng tập trung quanh giá trị trung bình.
Lời giải chi tiết
a) Theo bảng, ta có N = 4 + 12 + 16 + 14 + 2 + 2 = 50.
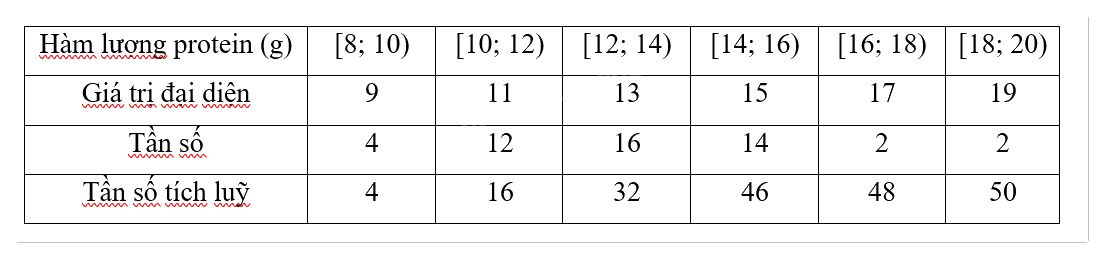
Khoảng biến thiên:
R = Giá trị lớn nhất – Giá trị nhỏ nhất = 20 – 8 = 12
Tính tứ phân vị
- \(\frac{N}{4} = 12,5\) rơi vào nhóm [10; 12)
\({Q_1} = 10 + \left( {\frac{{12,5 - 4}}{{12}}} \right) \times 2 = 10 + 1,42 = 11,42{\mkern 1mu} {\rm{g}}\)
- \(\frac{{3N}}{4} = 37,5\) rơi vào nhóm [14; 16)
\({Q_3} = 14 + \left( {\frac{{37,5 - 32}}{{14}}} \right) \times 2 = 14 + 0,79 = 14,79{\mkern 1mu} {\rm{g}}\)
Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 14,79 - 11,42 = 3,37{\mkern 1mu} {\rm{g}}\)
Giá trị trung bình:
\(\bar x = \frac{1}{N}\sum\limits_{i = 1}^k {{f_i}} \times {x_i} = \frac{{4 \times 9 + 12 \times 11 + 16 \times 13 + 14 \times 15 + 2 \times 17 + 2 \times 19}}{{50}} \approx 13,16g\)
Độ lệch chuẩn của khối lượng những quả trứng này:
\(S = \sqrt {\frac{1}{{50}}\sum\limits_{i = 1}^6 {{f_i}} \times {{({x_i} - 12.98)}^2}} \)
\(S = \sqrt {\frac{1}{{50}}\left[ {4 \times {{(9 - 13.16)}^2} + 12 \times {{(11 - 13.16)}^2} + 16 \times {{(13 - 13.16)}^2} + 14 \times {{(15 - 13.16)}^2} + 2 \times {{(17 - 13.16)}^2} + 2 \times {{(19 - 13.16)}^2}} \right]} \)
\(S = \sqrt {\frac{1}{{50}} \times 270.72} \approx \sqrt {5.41} \approx 2.33\)
b) Ý nghĩa của các kết quả tìm được
Khoảng biến thiên (12 gram): Khoảng biến thiên đo lường sự khác biệt giữa giá trị lớn nhất và giá trị nhỏ nhất trong dữ liệu. Với khoảng biến thiên là 12, chúng ta biết rằng hàm lượng protein của các thực phẩm trong mẫu này dao động trong khoảng 12 gram.
Khoảng tứ phân vị (3,37 gram): Dữ liệu tập trung chủ yếu trong khoảng 3,37gram của tứ phân vị thứ nhất và thứ ba, cho thấy sự phân tán trung bình của hàm lượng protein trong các thực phẩm.
Giá trị trung bình cung cấp một ước lượng tổng quát về hàm lượng protein trung bình của các thực phẩm trong mẫu. Với giá trị trung bình là 13.16 gram, chúng ta có thể nói rằng, trung bình, mỗi thực phẩm trong mẫu có hàm lượng protein xấp xỉ 13.16 gram.
Độ lệch chuẩn đo lường mức độ phân tán của các giá trị dữ liệu xung quanh giá trị trung bình. Với độ lệch chuẩn là 2.33 gram, chúng ta biết rằng hàm lượng protein của các thực phẩm trong mẫu có sự phân tán trung bình khoảng 2.33 gram so với giá trị trung bình. Độ lệch chuẩn nhỏ hơn cho thấy dữ liệu tập trung gần giá trị trung bình, trong khi độ lệch chuẩn lớn hơn cho thấy sự phân tán rộng hơn.
Giải Bài Tập 3.12 Trang 104 SGK Toán 12 Tập 1: Phân Tích Chi Tiết và Phương Pháp Giải
Bài tập 3.12 trang 104 SGK Toán 12 tập 1 thường thuộc chủ đề về đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm ẩn. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
- Quy tắc đạo hàm: Nắm vững các quy tắc đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương, hàm hợp.
- Đạo hàm của hàm số lượng giác: Biết đạo hàm của các hàm số lượng giác sin, cos, tan, cot.
- Đạo hàm của hàm số mũ và logarit: Nắm vững đạo hàm của các hàm số mũ và logarit.
- Đạo hàm của hàm ẩn: Biết cách tìm đạo hàm của hàm ẩn bằng phương pháp lấy đạo hàm hai vế.
Nội Dung Bài Tập 3.12 Trang 104 SGK Toán 12 Tập 1 (Ví dụ)
Giả sử bài tập 3.12 có nội dung như sau:
Cho hàm số y = f(x) = sin2x. Tính f'(x).
Lời Giải Chi Tiết
Để tính f'(x), ta sử dụng quy tắc đạo hàm của hàm hợp:
f'(x) = 2sin(x) * cos(x) = sin(2x)
Giải thích:
- Ta xem hàm số y = f(x) = sin2x là hàm hợp g(u) = u2 với u = sin(x).
- Áp dụng quy tắc đạo hàm của hàm hợp: f'(x) = g'(u) * u'(x) = 2u * cos(x)
- Thay u = sin(x) vào, ta được: f'(x) = 2sin(x) * cos(x)
- Sử dụng công thức lượng giác sin(2x) = 2sin(x)cos(x), ta có: f'(x) = sin(2x)
Các Dạng Bài Tập Liên Quan và Phương Pháp Giải
Ngoài bài tập tính đạo hàm trực tiếp, bài tập 3.12 và các bài tập lân cận thường xuất hiện các dạng bài sau:
- Tìm đạo hàm cấp hai: Tính f''(x) sau khi đã tìm được f'(x).
- Ứng dụng đạo hàm để giải các bài toán về cực trị: Tìm các điểm cực trị của hàm số bằng cách giải phương trình f'(x) = 0.
- Ứng dụng đạo hàm để giải các bài toán về khoảng đơn điệu: Xác định khoảng đồng biến, nghịch biến của hàm số dựa vào dấu của f'(x).
- Ứng dụng đạo hàm để giải các bài toán về giá trị lớn nhất, giá trị nhỏ nhất: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Mẹo Giải Bài Tập Đạo Hàm Nhanh Chóng
- Nắm vững các công thức đạo hàm cơ bản: Điều này giúp bạn tiết kiệm thời gian và tránh sai sót.
- Sử dụng quy tắc đạo hàm một cách linh hoạt: Áp dụng quy tắc đạo hàm phù hợp với từng dạng bài tập.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Luyện tập thường xuyên: Luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập.
Tusach.vn – Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn đồng hành cùng các bạn học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Công thức | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sin(x) | y' = cos(x) |
| Bảng công thức đạo hàm cơ bản | |