Giải bài tập 5.41 trang 85 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải bài tập 5.41 trang 85 SGK Toán 12 tập 2
Bài tập 5.41 trang 85 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học. Bài toán này thường liên quan đến việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
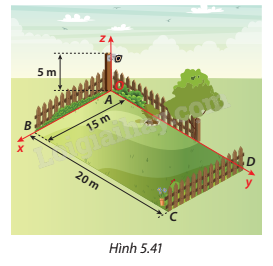
Một sân hình chữ nhật ABCD có chiều dài AD = 20 m, chiều rộng AB = 15 m. Người ta đặt một camera ở độ cao 5 m trên một cây cột vuông góc với mặt sân tại A, biết camera có bán kính quan sát là 25 m. Xét hệ trục toạ độ Oxyz với gốc toạ độ O trùng với điểm A chân cột, các tia Ox, Oy lần lượt chứa các cạnh AB, AD của sân và tia Oz chứa cây cột.
Đề bài
Một sân hình chữ nhật ABCD có chiều dài AD = 20 m, chiều rộng AB = 15 m. Người ta đặt một camera ở độ cao 5 m trên một cây cột vuông góc với mặt sân tại A, biết camera có bán kính quan sát là 25 m. Xét hệ trục toạ độ Oxyz với gốc toạ độ O trùng với điểm A chân cột, các tia Ox, Oy lần lượt chứa các cạnh AB, AD của sân và tia Oz chứa cây cột.
a) Viết phương trình mặt cầu mô tả ranh giới bên ngoài và bên trong của vùng quan sát được.
b) Hỏi camera có thể quan sát toàn bộ sân hay không? Vì sao?
Phương pháp giải - Xem chi tiết
- Xác định toạ độ các đỉnh của sân hình chữ nhật và của camera
- Lập phương trình mặt cầu:
Sử dụng công thức phương trình mặt cầu với tâm \(I({x_0},{y_0},{z_0})\) và bán kính R:
\({(x - {x_0})^2} + {(y - {y_0})^2} + {(z - {z_0})^2} = {R^2}\)
- Xác định tọa độ các đỉnh của sân và kiểm tra xem chúng có nằm trong phạm vi vùng quan sát của camera hay không.
- Một điểm \(M(x,y,z)\) nằm trong vùng quan sát nếu khoảng cách từ M đến I nhỏ hơn hoặc bằng R.
Lời giải chi tiết
a) Viết phương trình mặt cầu mô tả vùng quan sát
- Các điểm của sân: \(A(0;0;0)\), \(B(15;0;0)\), \(D(0;20;0)\), \(C(15;20;0)\)
- Camera đặt tại điểm \(I(0,0,5)\), độ cao \(z = 5\) m trên mặt sân tại điểm A.
- Bán kính quan sát của camera là \(R = 25\) m.
Lập phương trình mặt cầu:
- Sử dụng công thức phương trình mặt cầu với tâm \(I(0,0,5)\) và bán kính \(R = 25\):
\({(x - 0)^2} + {(y - 0)^2} + {(z - 5)^2} = {25^2}\)
\({x^2} + {y^2} + {(z - 5)^2} = 625\)
- Đây là phương trình mặt cầu mô tả ranh giới vùng quan sát của camera.
b) Kiểm tra khả năng quan sát toàn bộ sân
* Tính khoảng cách từ các đỉnh của sân đến camera:
- Khoảng cách từ I đến A:
\(IA = \sqrt {{{(0 - 0)}^2} + {{(0 - 0)}^2} + {{(5 - 0)}^2}} = 5{\mkern 1mu} {\rm{m}}\)
- Khoảng cách từ I đến B:
\(IB = \sqrt {{{(15 - 0)}^2} + {{(0 - 0)}^2} + {{(0 - 5)}^2}} = \sqrt {225 + 25} = \sqrt {250} \approx 15.81{\mkern 1mu} {\rm{m}}\)
- Khoảng cách từ I đến D:
\(ID = \sqrt {{{(0 - 0)}^2} + {{(20 - 0)}^2} + {{(0 - 5)}^2}} = \sqrt {400 + 25} = \sqrt {425} \approx 20.62{\mkern 1mu} {\rm{m}}\)
- Khoảng cách từ I đến C:
\(IC = \sqrt {{{(15 - 0)}^2} + {{(20 - 0)}^2} + {{(0 - 5)}^2}} = \sqrt {225 + 400 + 25} = \sqrt {650} \approx 25.5{\mkern 1mu} {\rm{m}}\)
- Camera có thể quan sát được toàn bộ sân nếu tất cả các đỉnh đều nằm trong bán kính quan sát. Ta thấy rằng khoảng cách \(IC \approx 25.5{\mkern 1mu} {\rm{m}} > 25{\mkern 1mu} {\rm{m}}\). Do đó, điểm C nằm ngoài phạm vi quan sát của camera.
Giải bài tập 5.41 trang 85 SGK Toán 12 tập 2: Hướng dẫn chi tiết và phương pháp giải
Bài tập 5.41 trang 85 SGK Toán 12 tập 2 thuộc chương trình Giải tích, cụ thể là phần ứng dụng đạo hàm để khảo sát hàm số. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm bậc nhất, đạo hàm bậc hai để xác định cực trị, khoảng đồng biến, nghịch biến của hàm số, từ đó giải quyết các bài toán liên quan đến tối ưu hóa.
Nội dung bài tập 5.41 trang 85 SGK Toán 12 tập 2
Thông thường, bài tập 5.41 sẽ đưa ra một hàm số và yêu cầu:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất và bậc hai của hàm số.
- Tìm các điểm cực trị của hàm số.
- Xác định khoảng đồng biến, nghịch biến của hàm số.
- Vẽ đồ thị hàm số (nếu cần).
- Giải các bài toán liên quan đến giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Phương pháp giải bài tập 5.41 trang 85 SGK Toán 12 tập 2
- Bước 1: Xác định tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Bước 2: Tính đạo hàm bậc nhất (y'). Sử dụng các quy tắc đạo hàm cơ bản để tính đạo hàm của hàm số.
- Bước 3: Tìm các điểm cực trị. Giải phương trình y' = 0 để tìm các điểm nghi ngờ là cực trị. Sau đó, xét dấu của y' để xác định loại cực trị (cực đại, cực tiểu).
- Bước 4: Tính đạo hàm bậc hai (y''). Sử dụng các quy tắc đạo hàm để tính đạo hàm bậc hai.
- Bước 5: Xác định khoảng đồng biến, nghịch biến. Xét dấu của y'. Nếu y' > 0 trên một khoảng, hàm số đồng biến trên khoảng đó. Nếu y' < 0 trên một khoảng, hàm số nghịch biến trên khoảng đó.
- Bước 6: Vẽ đồ thị hàm số (nếu cần). Dựa vào các thông tin đã tìm được (tập xác định, cực trị, khoảng đồng biến, nghịch biến) để vẽ đồ thị hàm số.
- Bước 7: Giải các bài toán liên quan đến giá trị lớn nhất, giá trị nhỏ nhất. Sử dụng các kiến thức về cực trị và khoảng đồng biến, nghịch biến để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Ví dụ minh họa (giả định bài tập cụ thể)
Giả sử bài tập 5.41 là: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và vẽ đồ thị.
Giải:
- Tập xác định: D = ℝ
- Đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Đạo hàm bậc hai: y'' = 6x - 6
- Xác định loại cực trị:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, y = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, y = -2
- Khoảng đồng biến, nghịch biến:
- Hàm số đồng biến trên (-∞, 0) và (2, +∞)
- Hàm số nghịch biến trên (0, 2)
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các bước tính toán đạo hàm.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.
- Hiểu rõ bản chất của các khái niệm đạo hàm, cực trị, khoảng đồng biến, nghịch biến.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài tập 5.41 trang 85 SGK Toán 12 tập 2 và các bài tập tương tự. Chúc các em học tốt!