Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 1.12 Trang 14 Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.12 trang 14 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về giới hạn của hàm số, một trong những kiến thức nền tảng quan trọng của môn Toán 12.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất
Đề bài
Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất
Phương pháp giải - Xem chi tiết
Bước 1: Lập công thức tính diện tích hình chữ nhật dưới dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính diện tích lớn nhất của hình chữ nhật là tìm gía trị lớn nhất của hàm số
Lời giải chi tiết
Gọi x là chiều dài hình chữ nhật (0<x<9)
Khi đó chiều rộng hình chữ nhật là 9 - x ( > 0)
Diện tích hình chữ nhật là S(x) = x( 9 - x )
Ta có \({\rm{S'(x) = 9 - 2x}}\)
Xét \({\rm{S'(x) = 0}}\) \( \Rightarrow {\rm{x = }}\frac{{\rm{9}}}{{\rm{2}}}\)
Ta có bảng biến thiên là
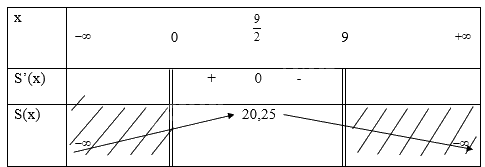
Vậy diện tích lớn nhất của hình chữ nhật là 20,25 khi chiều dài và chiều rộng bằng nhau và bằng \(\frac{{\rm{9}}}{{\rm{2}}}\)
Giải Bài Tập 1.12 Trang 14 Toán 12 Tập 1: Giới Hạn của Hàm Số
Bài tập 1.12 trang 14 SGK Toán 12 tập 1 yêu cầu chúng ta tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các phương pháp tính giới hạn thường gặp.
Nội dung bài tập 1.12:
Bài tập thường có dạng tính limx→a f(x), trong đó f(x) là một hàm số và a là một số thực hoặc vô cực.
Phương pháp giải bài tập 1.12:
- Kiểm tra dạng vô định: Nếu khi thay x = a vào hàm số f(x) ta được một trong các dạng 0/0, ∞/∞, ∞ - ∞, 0 * ∞ thì ta cần biến đổi hàm số để khử dạng vô định.
- Phân tích thành nhân tử: Nếu hàm số f(x) là một phân thức, ta có thể phân tích tử và mẫu thành nhân tử để rút gọn biểu thức.
- Sử dụng các công thức giới hạn: Áp dụng các công thức giới hạn cơ bản như limx→0 sinx/x = 1, limx→0 (1+x)1/x = e.
- Sử dụng quy tắc L'Hopital: Nếu bài toán có dạng 0/0 hoặc ∞/∞, ta có thể áp dụng quy tắc L'Hopital để tính giới hạn.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tính limx→2 (x2 - 4) / (x - 2). Ta có thể phân tích tử thành nhân tử như sau:
(x2 - 4) = (x - 2)(x + 2)
Khi đó, biểu thức trở thành:
limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Lưu ý quan trọng:
- Luôn kiểm tra kỹ điều kiện xác định của hàm số trước khi tính giới hạn.
- Sử dụng các công thức và quy tắc giới hạn một cách chính xác.
- Thực hành nhiều bài tập để nắm vững phương pháp giải.
Tài liệu tham khảo:
Ngoài SGK Toán 12 tập 1, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến uy tín
- Các video hướng dẫn giải bài tập Toán 12 trên YouTube
Hy vọng với lời giải chi tiết và phương pháp giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 này, các em sẽ hiểu rõ hơn về giới hạn của hàm số và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
| Công thức giới hạn quan trọng | Mô tả |
|---|---|
| limx→0 sinx/x = 1 | Giới hạn của sinx khi x tiến tới 0 bằng 1. |
| limx→0 (1+x)1/x = e | Giới hạn của (1+x)1/x khi x tiến tới 0 bằng số e. |