Giải Bài Tập 5.33 Trang 77 Toán 12 Tập 2

Giải bài tập 5.33 trang 77 SGK Toán 12 tập 2 - Cùng khám phá

Bài tập 5.33 trang 77 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học. Bài tập này thường liên quan đến việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.

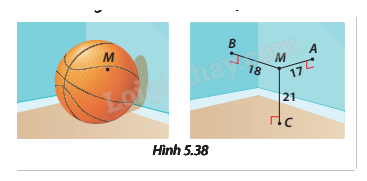
Bạn Bình đố bạn Nam tìm được đường kính của quả bóng rổ, biết rằng nếu đặt quả bóng ở một góc căn phòng hình hộp chữ nhật, sao cho quả bóng chạm (tiếp xúc) với hai bức tường và nền nhà của căn phòng đó (khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng) thì có một điểm M trên quả bóng với khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm và 21 cm (Hình 5.38). Hãy giúp Nam xác định đường kính của quả bóng rổ. Biết rằng loại bóng rổ tiêu chuẩn

Đề bài

Hãy giúp Nam xác định đường kính của quả bóng rổ. Biết rằng loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm.

Giải bài tập 5.33 trang 77 SGK Toán 12 tập 2 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 5.33 trang 77 SGK Toán 12 tập 2 - Cùng khám phá 2

- Xác định gốc toạ độ từ đó suy ra toạ độ của điểm M và tâm của quả bóng.

- Tính bán kính của quả bóng dựa trên các dữ kiện liên quan đến bán kính được cho ở đề bài.

Lời giải chi tiết

Đặt toạ độ O tại vị trí giao nhau giữa hai bức tường và nền nhà.

Toạ độ tương ứng với điểm M là \((17;18;21)\)

Gọi \(I(x;y;z)\) là tâm của quả bóng.

Vì khoảng cách từ tâm quả bóng đến hai bức tường và nền nhà đều bằng bán kính của quả bóng nên ta có: \(r = x = y = z\)

Suy ra I có toạ độ là \(I(r;r;r)\)

Do M nằm trên bề mặt quả bóng nên khoảng cách từ tâm I của quả bóng tới M chính là bán kính r, nên:

\(\begin{array}{l}\sqrt {{{(r - 17)}^2} + {{(r - 18)}^2} + {{(r - 21)}^2}} = r\\ \Leftrightarrow {r^2} - 34r + 289 + {r^2} - 36r + 324 + {r^2} - 42r + 441 = {r^2}\\ \Leftrightarrow 2{r^2} - 112r + 1054 = 0\end{array}\)

Từ phương trình trên ta thu được hai giá trị \({r_1} \approx 44,03\)và \({r_2} \approx 11,97\).

Vì loại bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm nên ta loại giá trị \({r_1}\) và nhận giá trị \({r_2}\) làm bán kính của quả bóng.

Vậy đường kính của bóng rổ là 23,94 cm.

Giải Bài Tập 5.33 Trang 77 SGK Toán 12 Tập 2: Hướng Dẫn Chi Tiết

Bài tập 5.33 trang 77 SGK Toán 12 tập 2 thường thuộc chủ đề về ứng dụng đạo hàm để khảo sát hàm số. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, cực trị, và điểm uốn của hàm số.

Phân Tích Đề Bài và Xác Định Yêu Cầu

Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài tập 5.33 sẽ yêu cầu chúng ta:

Tìm tập xác định của hàm số.
Tính đạo hàm bậc nhất và bậc hai của hàm số.
Xác định các điểm cực trị của hàm số.
Xác định khoảng đồng biến và nghịch biến của hàm số.
Tìm điểm uốn của hàm số.
Vẽ đồ thị hàm số.

Lời Giải Chi Tiết Bài Tập 5.33

Để minh họa, giả sử bài tập 5.33 có nội dung như sau:

Cho hàm số y = x³ - 3x² + 2. Hãy khảo sát hàm số và vẽ đồ thị.

Tìm tập xác định: Hàm số y = x³ - 3x² + 2 có tập xác định là D = ℝ.
Tính đạo hàm:
- y' = 3x² - 6x
- y'' = 6x - 6
Tìm cực trị:
- Giải phương trình y' = 0: 3x² - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
- Xét dấu y':
  x -∞ 0 2 +∞
  y' + - +
  y ↗ ↘ ↗
- Kết luận: Hàm số đạt cực đại tại x = 0, y_CĐ = 2 và đạt cực tiểu tại x = 2, y_CT = -2.
Tìm khoảng đồng biến, nghịch biến:
- Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- Hàm số nghịch biến trên khoảng (0; 2).
Tìm điểm uốn:
- Giải phương trình y'' = 0: 6x - 6 = 0 ⇔ x = 1
- Xét dấu y'':
  x -∞ 1 +∞
  y'' - +
  y ∩ ∪
- Kết luận: Hàm số có điểm uốn tại x = 1, y_U = 0.
Vẽ đồ thị: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số y = x³ - 3x² + 2.

x	-∞	0	2	+∞
y'	+	-	+
y	↗	↘	↗

x	-∞	1	+∞
y''	-	+
y	∩	∪

Lưu Ý Khi Giải Bài Tập

Khi giải các bài tập về ứng dụng đạo hàm, cần lưu ý:

Nắm vững các định nghĩa và tính chất của đạo hàm.
Sử dụng các quy tắc tính đạo hàm một cách chính xác.
Phân tích kỹ đề bài và xác định rõ yêu cầu.
Kiểm tra lại kết quả sau khi giải xong.

Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải quyết bài tập 5.33 trang 77 SGK Toán 12 tập 2 và các bài tập tương tự. Chúc các em học tốt!

Giải bài tập 5.33 trang 77 SGK Toán 12 tập 2 - Cùng khám phá