Giải mục 2 trang 58, 59, 60 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải mục 2 trang 58, 59, 60 SGK Toán 12 tập 1
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 58, 59, 60 SGK Toán 12 tập 1 trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, tusach.vn đã biên soạn và trình bày lời giải bài tập một cách rõ ràng, dễ hiểu, kèm theo các lưu ý quan trọng.
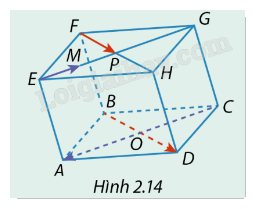
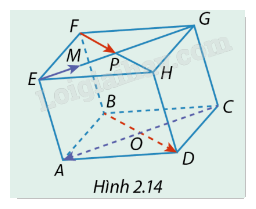
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ: a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \). b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
VD2
Trả lời câu hỏi Vận dụng 2 trang 59 SGK Toán 12 Cùng khám phá
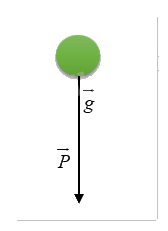
Trọng lực \(\vec P\) là lực hấp dẫn do Trái Đất tác dụng lên một vật, được tính theo công thức \(\vec P = m\vec g\), trong đó \(m\) là khối lượng của vật (đơn vị: kg), còn \(\vec g\) là vectơ gia tốc rơi tự do, có hướng đi xuống và có độ lớn \(g = 9,8{\mkern 1mu} m/{s^2}\). Xác định hướng và độ lớn của trọng lực (đơn vị: N) tác dụng lên quả bưởi có khối lượng \(2,5{\mkern 1mu} kg\).
Phương pháp giải:
- Sử dụng công thức tính trọng lực: \(\vec P = m\vec g\)
- Thay các giá trị đã cho vào công thức để tính toán.
Lời giải chi tiết:
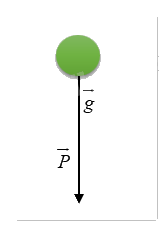
- Khối lượng của quả bưởi: \(m = 2,5{\mkern 1mu} kg\).
- Gia tốc rơi tự do: \(g = 9,8{\mkern 1mu} m/{s^2}\).
- Trọng lực tác dụng lên quả bưởi được tính theo công thức: \(P = m \cdot g\).
- Thay các giá trị vào: \(P = 2,5 \times 9,8 = 24,5{\mkern 1mu} N\).
- Hướng của trọng lực: Hướng xuống dưới (theo chiều của vectơ \(\vec g\)).
Kết luận:
- Độ lớn của trọng lực tác dụng lên quả bưởi là \(24,5{\mkern 1mu} N\).
- Hướng của trọng lực là hướng xuống dưới.
LT5
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
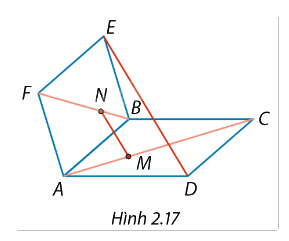
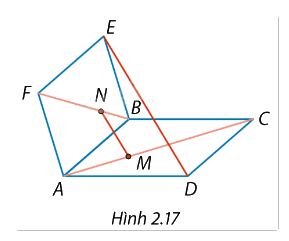
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên các đường chéo AC và BF lấy các điểm \(M\), \(N\) sao cho \(MC = 2MA\), \(NF = 2NB\) (Hình 2.17).
a) Biểu diễn các vectơ \(\overrightarrow {MN} \), \(\overrightarrow {DE} \) theo \(\overrightarrow {AB} \), \(\overrightarrow {AD} \), \(\overrightarrow {AF} \).
b) Từ đó suy ra MN//DE.
Phương pháp giải:
a) Áp dụng quy tắc ba điểm và quy tắc hình bình hành kết hợp với các tính chất của phép nhân một số với một vectơ.
b) Tìm k (k≠0) sao cho \(\overrightarrow {MN} = k\overrightarrow {DE} \)thì hai vectơ đó song song.
Lời giải chi tiết:
a)
Do \(MC = 2MA\), \(NF = 2NB\) nên \(\overrightarrow {AC} = - 3\overrightarrow {MA}, \overrightarrow {FB} = \frac{2}{3}\overrightarrow {FN} \).
- Biểu diễn \(\overrightarrow {MN} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {MN} \): \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - \frac{1}{3}\overrightarrow {AC} + \overrightarrow {AF} + \frac{2}{3}\overrightarrow {FB} (*)\)
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {FA} + \overrightarrow {FE} = \overrightarrow {FB} \)
Thay vào (*) ta có:
\(\overrightarrow {MN} = - \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AF} + \frac{2}{3}(\overrightarrow {FA} + \overrightarrow {FE} ) = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} + \frac{2}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} \)
\(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {AF} } \right)\)
- Biểu diễn \(\overrightarrow {DE} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {DE} \):
\(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - \overrightarrow {AD} + \overrightarrow {AB} + \overrightarrow {AF} \)
b) Từ câu a ta thấy \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {DE} \) suy ra MN // DE.
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ:
a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \).
b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
Phương pháp giải:
- Kiểm tra xem hai vectơ có cùng phương hay không (cùng phương, ngược phương hay không cùng phương).
- Tính độ dài của các vectơ để so sánh.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \):
Vì ABCD.EFGH là hình hộp nên \(\overrightarrow {BD} = \overrightarrow {FH} \) (cùng hướng và có độ dài bằng nhau vì đều là đường chéo của hai đáy hình hộp).
Lại có: \(FP = \frac{1}{2}FH\)do P là trung điểm của PH nên \(\overrightarrow {FP} = \frac{1}{2}\overrightarrow {FH} \).
Suy ra: \(\overrightarrow {BD} = 2\overrightarrow {FP} \).
b) Vectơ \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \):
Tương tự, vì ABCD.EFGH là hình hộp nên \(\overrightarrow {CA} = \overrightarrow {GE} \).
Lại có: \(EM = \frac{1}{2}EP = \frac{1}{4}GE\)mà \(\overrightarrow {EM} \) ngược hướng với \(\overrightarrow {GE} \) nên \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {GE} \).
Suy ra: \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {CA} \).
LT4
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
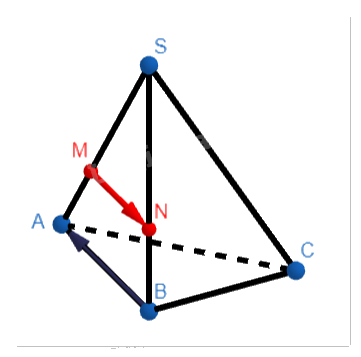
Cho hình chóp S.ABC. Điểm \(M\) thuộc cạnh SA và \(SM = \frac{2}{3}SA\).
a) Viết hệ thức liên hệ giữa các cặp vectơ \(\overrightarrow {SM} \) và \(\overrightarrow {SA} \), \(\overrightarrow {MA} \) và \(\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Phương pháp giải:
a) Sử dụng định nghĩa và tính chất của vectơ để thiết lập các mối quan hệ giữa các vectơ đã cho.
b) Sử dụng hệ thức liên quan đến vectơ để tìm tọa độ của điểm N thỏa mãn điều kiện đã cho.
Lời giải chi tiết:
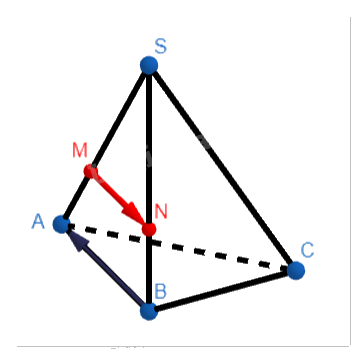
a) Ta có: \(SM = \frac{2}{3}SA \Rightarrow \overrightarrow {SM} = \frac{2}{3}\overrightarrow {SA} \).
Vì \(M\) thuộc SA, nên \(MA = SA - SM\). Do đó:
\(\overrightarrow {MA} = \overrightarrow {SA} - \overrightarrow {SM} = \overrightarrow {SA} - \frac{2}{3}\overrightarrow {SA} = \frac{1}{3}\overrightarrow {SA} \).
Ta cũng có: \(\overrightarrow {AS} = - \overrightarrow {SA} \).
Suy ra: \(\overrightarrow {MA} = - \frac{1}{3}\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Ta có: \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \to \overrightarrow {MN} = \frac{2}{3}\overrightarrow {AB} \).
Suy ra: \(MN//AB;MN = \frac{2}{3}AB\).
Tam giác SAB có đoạn thẳng MN song song với AB và \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\) thì từ định lý Talet ta suy ra N thuộc cạnh SB:
\(\frac{{SN}}{{SB}} = \frac{2}{3} \Leftrightarrow SN = \frac{2}{3}SB\).
- HĐ4
- LT4
- VD2
- LT5
Trả lời câu hỏi Hoạt động 4 trang 58 SGK Toán 12 Cùng khám phá
Cho hình hộp ABCD.EFGH có O và P tương ứng là giao điểm các đường chéo của hai đáy ABCD và EFGH. M là trung điểm của đoạn thẳng EP (Hình 2.14). Xét mối quan hệ về hướng và độ dài của các cặp vectơ:
a) \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \).
b) \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \).
Phương pháp giải:
- Kiểm tra xem hai vectơ có cùng phương hay không (cùng phương, ngược phương hay không cùng phương).
- Tính độ dài của các vectơ để so sánh.
Lời giải chi tiết:
a) Vectơ \(\overrightarrow {BD} \) và \(\overrightarrow {FP} \):
Vì ABCD.EFGH là hình hộp nên \(\overrightarrow {BD} = \overrightarrow {FH} \) (cùng hướng và có độ dài bằng nhau vì đều là đường chéo của hai đáy hình hộp).
Lại có: \(FP = \frac{1}{2}FH\)do P là trung điểm của PH nên \(\overrightarrow {FP} = \frac{1}{2}\overrightarrow {FH} \).
Suy ra: \(\overrightarrow {BD} = 2\overrightarrow {FP} \).
b) Vectơ \(\overrightarrow {EM} \) và \(\overrightarrow {CA} \):
Tương tự, vì ABCD.EFGH là hình hộp nên \(\overrightarrow {CA} = \overrightarrow {GE} \).
Lại có: \(EM = \frac{1}{2}EP = \frac{1}{4}GE\)mà \(\overrightarrow {EM} \) ngược hướng với \(\overrightarrow {GE} \) nên \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {GE} \).
Suy ra: \(\overrightarrow {EM} = - \frac{1}{4}\overrightarrow {CA} \).
Trả lời câu hỏi Luyện tập 4 trang 59 SGK Toán 12 Cùng khám phá
Cho hình chóp S.ABC. Điểm \(M\) thuộc cạnh SA và \(SM = \frac{2}{3}SA\).
a) Viết hệ thức liên hệ giữa các cặp vectơ \(\overrightarrow {SM} \) và \(\overrightarrow {SA} \), \(\overrightarrow {MA} \) và \(\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Phương pháp giải:
a) Sử dụng định nghĩa và tính chất của vectơ để thiết lập các mối quan hệ giữa các vectơ đã cho.
b) Sử dụng hệ thức liên quan đến vectơ để tìm tọa độ của điểm N thỏa mãn điều kiện đã cho.
Lời giải chi tiết:
a) Ta có: \(SM = \frac{2}{3}SA \Rightarrow \overrightarrow {SM} = \frac{2}{3}\overrightarrow {SA} \).
Vì \(M\) thuộc SA, nên \(MA = SA - SM\). Do đó:
\(\overrightarrow {MA} = \overrightarrow {SA} - \overrightarrow {SM} = \overrightarrow {SA} - \frac{2}{3}\overrightarrow {SA} = \frac{1}{3}\overrightarrow {SA} \).
Ta cũng có: \(\overrightarrow {AS} = - \overrightarrow {SA} \).
Suy ra: \(\overrightarrow {MA} = - \frac{1}{3}\overrightarrow {AS} \).
b) Tìm điểm \(N\) sao cho \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \).
Ta có: \(\overrightarrow {MN} = - \frac{2}{3}\overrightarrow {BA} \to \overrightarrow {MN} = \frac{2}{3}\overrightarrow {AB} \).
Suy ra: \(MN//AB;MN = \frac{2}{3}AB\).
Tam giác SAB có đoạn thẳng MN song song với AB và \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\) thì từ định lý Talet ta suy ra N thuộc cạnh SB:
\(\frac{{SN}}{{SB}} = \frac{2}{3} \Leftrightarrow SN = \frac{2}{3}SB\).
Trả lời câu hỏi Vận dụng 2 trang 59 SGK Toán 12 Cùng khám phá
Trọng lực \(\vec P\) là lực hấp dẫn do Trái Đất tác dụng lên một vật, được tính theo công thức \(\vec P = m\vec g\), trong đó \(m\) là khối lượng của vật (đơn vị: kg), còn \(\vec g\) là vectơ gia tốc rơi tự do, có hướng đi xuống và có độ lớn \(g = 9,8{\mkern 1mu} m/{s^2}\). Xác định hướng và độ lớn của trọng lực (đơn vị: N) tác dụng lên quả bưởi có khối lượng \(2,5{\mkern 1mu} kg\).
Phương pháp giải:
- Sử dụng công thức tính trọng lực: \(\vec P = m\vec g\)
- Thay các giá trị đã cho vào công thức để tính toán.
Lời giải chi tiết:
- Khối lượng của quả bưởi: \(m = 2,5{\mkern 1mu} kg\).
- Gia tốc rơi tự do: \(g = 9,8{\mkern 1mu} m/{s^2}\).
- Trọng lực tác dụng lên quả bưởi được tính theo công thức: \(P = m \cdot g\).
- Thay các giá trị vào: \(P = 2,5 \times 9,8 = 24,5{\mkern 1mu} N\).
- Hướng của trọng lực: Hướng xuống dưới (theo chiều của vectơ \(\vec g\)).
Kết luận:
- Độ lớn của trọng lực tác dụng lên quả bưởi là \(24,5{\mkern 1mu} N\).
- Hướng của trọng lực là hướng xuống dưới.
Trả lời câu hỏi Luyện tập 5 trang 60 SGK Toán 12 Cùng khám phá
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên các đường chéo AC và BF lấy các điểm \(M\), \(N\) sao cho \(MC = 2MA\), \(NF = 2NB\) (Hình 2.17).
a) Biểu diễn các vectơ \(\overrightarrow {MN} \), \(\overrightarrow {DE} \) theo \(\overrightarrow {AB} \), \(\overrightarrow {AD} \), \(\overrightarrow {AF} \).
b) Từ đó suy ra MN//DE.
Phương pháp giải:
a) Áp dụng quy tắc ba điểm và quy tắc hình bình hành kết hợp với các tính chất của phép nhân một số với một vectơ.
b) Tìm k (k≠0) sao cho \(\overrightarrow {MN} = k\overrightarrow {DE} \)thì hai vectơ đó song song.
Lời giải chi tiết:
a)
Do \(MC = 2MA\), \(NF = 2NB\) nên \(\overrightarrow {AC} = - 3\overrightarrow {MA}, \overrightarrow {FB} = \frac{2}{3}\overrightarrow {FN} \).
- Biểu diễn \(\overrightarrow {MN} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {MN} \): \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - \frac{1}{3}\overrightarrow {AC} + \overrightarrow {AF} + \frac{2}{3}\overrightarrow {FB} (*)\)
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {FA} + \overrightarrow {FE} = \overrightarrow {FB} \)
Thay vào (*) ta có:
\(\overrightarrow {MN} = - \frac{1}{3}(\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AF} + \frac{2}{3}(\overrightarrow {FA} + \overrightarrow {FE} ) = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} + \frac{2}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {AF} \)
\(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {AB} - \overrightarrow {AD} + \overrightarrow {AF} } \right)\)
- Biểu diễn \(\overrightarrow {DE} \)
Sử dụng quy tắc ba điểm vào \(\overrightarrow {DE} \):
\(\overrightarrow {DE} = \overrightarrow {DA} + \overrightarrow {AE} = - \overrightarrow {AD} + \overrightarrow {AB} + \overrightarrow {AF} \)
b) Từ câu a ta thấy \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {DE} \) suy ra MN // DE.
Giải mục 2 trang 58, 59, 60 SGK Toán 12 tập 1: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 12 tập 1 thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học tiếp theo và các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chi tiết Giải mục 2 trang 58, 59, 60
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2, chúng ta sẽ đi vào phân tích chi tiết từng bài tập trên trang 58, 59 và 60.
Bài 1: Trang 58 - Tính đạo hàm của hàm số
Bài tập này yêu cầu các em vận dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số cho trước. Lưu ý khi giải bài tập này là cần nắm vững các công thức đạo hàm cơ bản và quy tắc chuỗi, quy tắc tích, quy tắc thương.
Ví dụ:
Cho hàm số y = x3 + 2x2 - 5x + 1. Tính y’.
Lời giải:
y’ = 3x2 + 4x - 5
Bài 2: Trang 59 - Tìm đạo hàm cấp hai
Bài tập này yêu cầu các em tìm đạo hàm cấp hai của hàm số, tức là đạo hàm của đạo hàm cấp nhất. Để giải bài tập này, các em cần thực hiện tuần tự các bước: tìm đạo hàm cấp nhất, sau đó tìm đạo hàm của đạo hàm cấp nhất để được đạo hàm cấp hai.
Ví dụ:
Cho hàm số y = sin(x). Tìm y’’.
Lời giải:
y’ = cos(x)
y’’ = -sin(x)
Bài 3: Trang 60 - Ứng dụng đạo hàm để tìm cực trị
Bài tập này yêu cầu các em sử dụng đạo hàm để tìm cực trị của hàm số. Để giải bài tập này, các em cần thực hiện các bước sau:
- Tìm tập xác định của hàm số.
- Tính đạo hàm cấp nhất y’.
- Giải phương trình y’ = 0 để tìm các điểm cực trị.
- Lập bảng biến thiên để xác định loại cực trị (cực đại, cực tiểu).
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các công thức đạo hàm cơ bản.
- Vận dụng linh hoạt các quy tắc tính đạo hàm.
- Kiểm tra lại kết quả sau khi tính toán.
- Sử dụng máy tính cầm tay để hỗ trợ tính toán.
Tại sao nên chọn tusach.vn để học Toán 12?
tusach.vn là một website học tập trực tuyến uy tín, cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm:
- Lời giải chi tiết các bài tập trong SGK và SBT.
- Các bài giảng video chất lượng cao.
- Các bài kiểm tra trắc nghiệm online.
- Diễn đàn trao đổi học tập sôi nổi.
Chúng tôi cam kết mang đến cho các em một môi trường học tập hiệu quả và thú vị. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp các công thức đạo hàm cơ bản
| Hàm số y | Đạo hàm y’ |
|---|---|
| y = c (hằng số) | y’ = 0 |
| y = xn | y’ = nxn-1 |
| y = sin(x) | y’ = cos(x) |
| y = cos(x) | y’ = -sin(x) |