Giải bài tập 5.29 trang 71 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 5.29 Trang 71 Toán 12 Tập 2
Bài tập 5.29 trang 71 SGK Toán 12 tập 2 là một bài toán quan trọng trong chương trình học. Bài toán này thường liên quan đến việc ứng dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
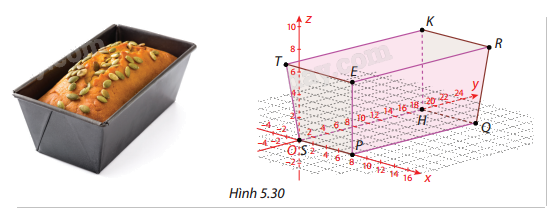
Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Đề bài
Một khuôn nướng bánh mì được mô phỏng trong không gian Oxyz như Hình 5.30 với các điểm sau: \(S(0;0;0)\), \(P(8;0;0)\), \(Q(8;18;0)\), \(T( - 1; - 1;7)\), \(R(9;19;7)\). Tính góc giữa hai cạnh kề nhau, giữa cạnh bên và mặt đáy, giữa mặt bên và mặt đáy của khuôn.
Phương pháp giải - Xem chi tiết
1. Tính góc giữa hai cạnh kề
- Xác định vectơ chỉ phương của hai cạnh:
- Sử dụng công thức tính góc giữa hai vectơ:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
2. Tính góc giữa cạnh bên và mặt đáy:
- Xác định các vectơ chỉ phương của cạnh bên và mặt đáy.
- Sử dụng công thức tính góc giữa hai vectơ:
\(\cos \theta = \frac{{\vec u \cdot \vec v}}{{|\vec u||\vec v|}}\)
3. Tính góc giữa mặt bên và mặt đáy:
- Tính vectơ pháp tuyến của mặt bên và mặt đáy.
- Sử dụng công thức tính góc giữa hai mặt phẳng:
\(\cos \theta = \frac{{|\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} |}}{{|\overrightarrow {{n_1}} ||\overrightarrow {{n_2}} |}}\)
Lời giải chi tiết
- Tính góc giữa hai cạnh kề nhau:
Ta có các vectơ chỉ phương sau:
\(\overrightarrow {SP} = P - S = (8 - 0;0 - 0;0 - 0) = (8;0;0)\)
\(\overrightarrow {SQ} = Q - S = (8 - 0;18 - 0;0 - 0) = (8;18;0)\)
\(\overrightarrow {ST} = T - S = ( - 1 - 0; - 1 - 0;7 - 0) = ( - 1; - 1;7)\)
\(\overrightarrow {SH} = \overrightarrow {PQ} = (0;18;0)\)
\(\overrightarrow {SE} = (9; - 1;7)\)
Góc giữa những cặp cạnh kề nhau:
\(\begin{array}{l}\cos (\overrightarrow {SP} ,\overrightarrow {ST} ) = \frac{{8.( - 1) + 0.( - 1) + 0.( - 7)}}{{\sqrt {{8^2}} .\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {{( - 7)}^2}} }} = \frac{{ - 8}}{{8.\sqrt {51} }} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {SP} ,\overrightarrow {ST} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {PS} ,\overrightarrow {PE} ) = (\overrightarrow {HQ} ,\overrightarrow {HK} ) = (\overrightarrow {QH} ,\overrightarrow {QR} ) \approx {98^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {EP} ,\overrightarrow {ER} ) = \frac{{( - 1).(0) + (1).(2) + ( - 7).(0)}}{{\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} .\sqrt {{0^2} + {2^2} + {0^2}} }} = \frac{2}{{\sqrt {51} .2}} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {EP} ,\overrightarrow {ER} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {RE} ,\overrightarrow {RQ} ) = (\overrightarrow {TS} ,\overrightarrow {TK} ) = (\overrightarrow {KT} ,\overrightarrow {KH} ) \approx {82^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {ET} ,\overrightarrow {EP} ) = \frac{{( - 10).( - 1) + (0).(1) + (0).( - 7)}}{{\sqrt {{{( - 10)}^2} + {0^2} + {0^2}} .\sqrt {{{( - 1)}^2} + {1^2} + {{( - 7)}^2}} }} = \frac{{10}}{{10.\sqrt {51} }} = \frac{1}{{\sqrt {51} }} \Rightarrow (\overrightarrow {ET} ,\overrightarrow {EP} ) \approx {82^\circ }\\ \Leftrightarrow (\overrightarrow {TE} ,\overrightarrow {TS} ) = (\overrightarrow {KH} ,\overrightarrow {KR} ) = (\overrightarrow {RK} ,\overrightarrow {RQ} ) \approx {82^\circ }\end{array}\)
\(\begin{array}{l}\cos (\overrightarrow {PE} ,\overrightarrow {PQ} ) = \frac{{(1).(0) + ( - 1).(18) + (7).(0)}}{{\sqrt {{1^2} + {{( - 1)}^2} + {7^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = \frac{{ - 18}}{{\sqrt {51} .18}} = \frac{{ - 1}}{{\sqrt {51} }} \Rightarrow (\overrightarrow {PE} ,\overrightarrow {PQ} ) \approx {98^\circ }\\ \Leftrightarrow (\overrightarrow {QP} ,\overrightarrow {QR} ) = (ST,\overrightarrow {SH} ) = (\overrightarrow {HS} ,\overrightarrow {HK} ) \approx {98^\circ }\end{array}\)
\(\cos (\overrightarrow {SP} ,\overrightarrow {SH} ) = \frac{{8.(0) + 0.(18) + 0.(0)}}{{\sqrt {{8^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {SP} ,\overrightarrow {SH} ) = {90^\circ }\)
\(\cos (\overrightarrow {PS} ,\overrightarrow {PQ} ) = \frac{{( - 8).(0) + 0.(18) + 0.(0)}}{{\sqrt {{{( - 8)}^2}} .\sqrt {{0^2} + {{18}^2} + {0^2}} }} = 0 \Rightarrow (\overrightarrow {PS} ,\overrightarrow {PQ} ) = {90^\circ }\)
Các cặp cạnh còn lại có số đo góc là 90°
- Tính góc giữa cạnh bên và mặt đáy:
Chọn một cạnh bên là ST.
Vectơ pháp tuyến của mặt đáy SPQH là:
\(\vec n = \overrightarrow {SP} \times \overrightarrow {SQ} = (0.0 - 0.18;0.8 - 8.0;8.18 - 0.8) = (0;0;144)\)
\( \Rightarrow \theta = \arccos \left( {\frac{7}{{\sqrt {51} }}} \right)\)
- Tính góc giữa mặt bên và mặt đáy của khuôn.
Chọn mặt bên là STEP
Vectơ pháp tuyến của mặt phẳng STEP là:
\(\overrightarrow {{n_{STEP}}} = \overrightarrow {SP} .\overrightarrow {ST} = (0.7 - 0.( - 1);0.( - 1) - 8.7;8.( - 1) - 0.( - 1)) = (0; - 56; - 8)\)
Góc giữa mặt bên STEP và mặt đáy SPQH là:
\(\cos \theta = \frac{{\left| {0.0 + 0.( - 56) + 144.( - 8)} \right|}}{{\sqrt {{{144}^2}} .\sqrt {{{( - 56)}^2} + {{( - 8)}^2}} }} = \frac{{1208}}{{144.40\sqrt 2 }} = \frac{{151}}{{720\sqrt 2 }} \Rightarrow \theta \approx 81^\circ \)
Giải Bài Tập 5.29 Trang 71 SGK Toán 12 Tập 2: Hướng Dẫn Chi Tiết
Bài tập 5.29 trang 71 SGK Toán 12 tập 2 thường thuộc chủ đề về ứng dụng đạo hàm để khảo sát hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, cực trị, và điểm uốn của hàm số.
Phân Tích Đề Bài
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài tập 5.29 sẽ yêu cầu chúng ta:
- Tìm tập xác định của hàm số.
- Tính đạo hàm bậc nhất và bậc hai của hàm số.
- Xác định các điểm cực trị của hàm số.
- Xác định khoảng đồng biến và nghịch biến của hàm số.
- Tìm điểm uốn của hàm số.
- Vẽ đồ thị hàm số.
Lời Giải Chi Tiết
Để minh họa, giả sử bài tập 5.29 có nội dung sau:
Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát hàm số và vẽ đồ thị.
- Tìm tập xác định: Hàm số y = x3 - 3x2 + 2 xác định trên tập số thực R.
- Tính đạo hàm:
- y' = 3x2 - 6x
- y'' = 6x - 6
- Tìm điểm cực trị:
Giải phương trình y' = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
Xét dấu y':
x -∞ 0 2 +∞ y' + - + Hàm số Đồng biến Nghịch biến Đồng biến Vậy hàm số đạt cực đại tại x = 0, yCĐ = 2 và đạt cực tiểu tại x = 2, yCT = -2.
- Tìm điểm uốn:
Giải phương trình y'' = 0: 6x - 6 = 0 => x = 1
Xét dấu y'':
x -∞ 1 +∞ y'' - + Đồ thị Lõm xuống Lõm lên Vậy hàm số có điểm uốn tại x = 1, yU = 0.
- Vẽ đồ thị: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số y = x3 - 3x2 + 2.
Lưu Ý Quan Trọng
Khi giải các bài tập về ứng dụng đạo hàm, cần chú ý:
- Kiểm tra kỹ điều kiện xác định của hàm số.
- Tính đạo hàm chính xác.
- Xét dấu đạo hàm một cách cẩn thận để xác định khoảng đồng biến, nghịch biến và cực trị.
- Sử dụng điểm uốn để vẽ đồ thị chính xác hơn.
Tusach.vn – Đồng Hành Cùng Bạn Học Toán
Tusach.vn luôn đồng hành cùng các bạn học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 2. Hãy truy cập Tusach.vn để khám phá thêm nhiều kiến thức hữu ích và nâng cao kết quả học tập của bạn!