Giải mục 1 trang 90, 91, 92, 93, 94, 95 SGK Toán 12 tập 2 - Cùng khám phá
Tổng quan nội dung
Giải mục 1 trang 90, 91, 92, 93, 94, 95 SGK Toán 12 tập 2
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 90, 91, 92, 93, 94, 95 sách giáo khoa Toán 12 tập 2. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em hiểu rõ kiến thức và tự tin giải quyết các bài tập.
Mục 1 này thường xoay quanh các chủ đề về đạo hàm, ứng dụng đạo hàm để khảo sát hàm số, hoặc các bài toán liên quan đến cực trị.
Một kho hàng chứa 80 sản phẩm cùng loại, bao gồm 30 sản phẩm do nhà máy I sản xuất (trong đó có 25 sản phẩm tốt, 5 sản phẩm kém chất lượng) và 50 sản phẩm do nhà máy II sản xuất (trong đó có 43 sản phẩm tốt, 7 sản phẩm kém chất lượng) như trong bảng (Bảng 6.1).
LT1
Trả lời câu hỏi Luyện tập 1 trang 92 SGK Toán 12 Cùng khám phá
Xét phép thử gieo một con xúc xắc cân đối đồng chất hai lần, quan sát số chấm xuất hiện trong mỗi lần gieo.
Tính xác suất để tổng số chấm trong hai lần gieo là 7, biết rằng lần gieo đầu tiên xuất hiện mặt 5 chấm.
Phương pháp giải:
Gọi A là biến cố "tổng số chấm là 7".
Gọi B là biến cố "lần gieo đầu xuất hiện 5 chấm".
Cần tính \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\).
Lời giải chi tiết:
* Xét không gian mẫu \(\Omega \):
- Mỗi lần gieo có 6 khả năng từ 1 đến 6 chấm
- Với 2 lần gieo độc lập, ta có \(|\Omega | = 6 \times 6 = 36\) phần tử
* Tính \(P(B)\):
- B là biến cố "lần gieo đầu xuất hiện 5 chấm"
- \(P(B) = \frac{1}{6}\) (vì xúc xắc cân đối)
* Tính \(P(AB)\):
- A là "tổng số chấm là 7"
- B là "lần đầu được 5 chấm"
- Do đã biết lần đầu được 5 chấm, muốn tổng là 7 thì lần 2 phải được 2 chấm. Gọi C là biến cố “lần hai được 2 chấm”
- \(P(AB) = P(B) \times P({\rm{C}}) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{{36}}\)
* Tính xác suất cần tìm \(P(A|B)\):
\(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}\)
Vậy xác suất để tổng số chấm trong hai lần gieo là 7, biết rằng lần gieo đầu tiên xuất hiện mặt 5 chấm là \(\frac{1}{6}\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 93 SGK Toán 12 Cùng khám phá
Trở lại Hoạt động đầu bài, sử dụng Bảng 6.1, hãy tính xác suất để lấy được sản phẩm tốt, biết rằng sản phẩm lấy được do nhà máy II sản suất.
Phương pháp giải:
Gọi A là biến cố "lấy được sản phẩm tốt".
Gọi C là biến cố "lấy được sản phẩm do nhà máy II sản xuất".
Cần tính \(P(A|C) = \frac{{P(AC)}}{{P(C)}}\).
Lời giải chi tiết:
* Từ Bảng 6.1, ta có:
- Tổng số sản phẩm là 80
- Nhà máy II có 50 sản phẩm, trong đó:
+ 43 sản phẩm tốt
+ 7 sản phẩm kém chất lượng
- Gọi A là biến cố "lấy được sản phẩm tốt"
- Gọi C là biến cố "lấy được sản phẩm do nhà máy II sản xuất"
* Tính \(P(C)\):
- \(P(C) = \frac{{50}}{{80}} = \frac{5}{8} = 0,625\)
* Tính \(P(AC)\):
\(P(AC) = \frac{{43}}{{80}} = 0,5375\)
* Tính xác suất cần tìm \(P(A|C)\):
\(P(A|C) = \frac{{P(AC)}}{{P(C)}} = \frac{{\frac{{43}}{{80}}}}{{\frac{5}{8}}} = \frac{{43}}{{50}} = 0,86\)
Vậy xác suất để lấy được sản phẩm tốt, biết rằng sản phẩm đó do nhà máy II sản xuất là \(\frac{{43}}{{50}} = 0,86\) hay 86%.
Khởi động
Trả lời câu hỏi Khởi động trang 90 SGK Toán 12 Cùng khám phá
Một kho hàng chứa 80 sản phẩm cùng loại, bao gồm 30 sản phẩm do nhà máy I sản xuất (trong đó có 25 sản phẩm tốt, 5 sản phẩm kém chất lượng) và 50 sản phẩm do nhà máy II sản xuất (trong đó có 43 sản phẩm tốt, 7 sản phẩm kém chất lượng) như trong bảng (Bảng 6.1).

Lấy ngẫu nhiên một sản phẩm trong các sản phẩm này.
a) Gọi A là biến cố "Lấy được sản phẩm tốt" và B là biến cố "Lấy được sản phẩm do nhà máy I sản xuất". Tính \(P(B)\), \(P(AB)\).
b) Giả sử biến cố B đã xảy ra, tức là lấy được sản phẩm do nhà máy I sản xuất, tính xác suất để sản phẩm lấy được này là sản phẩm tốt.
c) Hãy so sánh kết quả của câu b với tỉ số \(\frac{{P(AB)}}{{P(B)}}\).
Phương pháp giải:
a) Tính xác suất theo công thức cổ điển: P(A) = số trường hợp thuận lợi / số trường hợp có thể.
b) Với xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\) .
c) So sánh các kết quả.
Lời giải chi tiết:
a) Tính \(P(B)\) và \(P(AB)\):
Theo đề bài ta có 30 sản phẩm do nhà máy I sản xuất trên tổng số 80 sản phẩm, suy ra xác suất lấy được sản phẩm do nhà máy I sản xuất là:
\(P(B) = \frac{{30}}{{80}} = 0,375\)
Trong 30 sản phẩm do nhà máy I sản xuất có 25 sản phẩm tốt, suy ra xác suất lấy được sản phẩm tốt do nhà máy I sản xuất là:
\(P(AB) = \frac{{25}}{{80}} = 0,3125\)
b) Tính xác suất có điều kiện:
- Khi biết sản phẩm do nhà máy I sản xuất, ta chỉ quan tâm đến 30 sản phẩm của nhà máy I
- Trong 30 sản phẩm của nhà máy I có 25 sản phẩm tốt
- \(P(A|B) = \frac{{25}}{{30}} = \frac{5}{6} \approx 0,8333\)
c) So sánh \(P(A|B)\) với \(\frac{{P(AB)}}{{P(B)}}\):
\(\frac{{P(AB)}}{{P(B)}} = \frac{{0,3125}}{{0,375}} = \frac{{25}}{{30}} = \frac{5}{6} \approx 0,8333\)
Kết luận: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{5}{6}\)
LT3
Trả lời câu hỏi Luyện tập 3 trang 95 SGK Toán 12 Cùng khám phá
Công ty nước giải khát X tổ chức một chương trình khuyến mại như sau: Trong mỗi thùng 24 chai nước giải khát đều có hai chai trúng thưởng (giải thưởng được viết ở dưới nắp chai), người tham gia chương trình được mở nắp một cách ngẫu nhiên lần lượt hai chai trong một thùng. Tính xác suất để một người tham gia chương trình mở được cả hai chai đều trúng thưởng.

Phương pháp giải:
Sử dụng công thức xác suất của biến cố đồng thời.
Phân tích thành hai bước:
- Xác suất mở chai trúng thưởng đầu tiên.
- Xác suất mở chai trúng thưởng thứ hai (sau khi đã mở được chai trúng thưởng thứ nhất).
Lời giải chi tiết:
* Gọi các biến cố:
- \({A_1}\): chai mở đầu tiên trúng thưởng
- \({A_2}\): chai mở thứ hai trúng thưởng (sau khi chai đầu trúng thưởng)
- Cần tính \(P({A_1}{A_2})\)
Xác suất chai đầu tiên trúng thưởng:
\(P({A_1}) = \frac{2}{{24}} = \frac{1}{{12}}\)
- Xác suất chai thứ hai trúng thưởng khi chai đầu đã trúng:
\(P({A_2}|{A_1}) = \frac{1}{{23}}\)
(vì còn 1 chai trúng thưởng trong 23 chai còn lại)
\(P({A_1}{A_2}) = P({A_1}) \times P({A_2}|{A_1}) = \frac{1}{{12}} \times \frac{1}{{23}} = \frac{1}{{276}}\)
Vậy xác suất để một người tham gia chương trình mở được cả hai chai đều trúng thưởng là \(\frac{1}{{276}}\) (khoảng 0,36%).
VD
Trả lời câu hỏi Vận dụng trang 95 SGK Toán 12 Cùng khám phá
Quay trở lại phần Khỏi động đầu bài, xét tình huống người chơi đã chọn hộp 1 và người dẫn chương trình đã cho mở hộp 2. Kí hiệu \({A_1}\), \({A_2}\), \({A_3}\) lần lượt là các biến cố "Quả có trong hộp 1", "Quả có trong hộp 2", "Quả có trong hộp 3" và B là biến cố "Người dẫn chương trình mở hộp 2".
a) Hoàn tất sơ đồ hình cây sau:
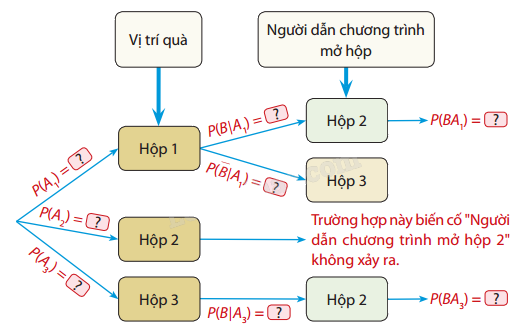
b) Tính \(P({A_1}|B)\) và \(P({A_3}|B)\). Từ đó cho biết người chơi nên giữ nguyên hộp mình đã lựa chọn ban đầu hay đổi số lựa chọn sang hộp khác thì cho khả năng lấy được quà cao hơn.
Phương pháp giải:
1. Xác định các xác suất từ sơ đồ hình cây
2. Sử dụng công thức xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\)
3. Tính \(P(B)\) bằng công thức xác suất toàn phần
4. So sánh \(P({A_1}|B)\) và \(P({A_3}|B)\) để đưa ra kết luận
Lời giải chi tiết:
a) Từ sơ đồ hình cây, ta có:
- \(P({A_1}) = P({A_2}) = P({A_3}) = \frac{1}{3}\) (xác suất ban đầu quà ở mỗi hộp)
- Khi quà ở hộp 1: \(P(B|{A_1}) = \frac{1}{2}\) (người dẫn chương trình có thể chọn mở hộp 2 hoặc 3). Suy ra xác suất để người dẫn chương trình mở hộp 2 và quà ở trong hộp 1 là \(P(B{A_1}) = P({A_1}).(B|{A_1}) = \frac{1}{3}.\frac{1}{2} = \frac{1}{6}\)
- Khi quà ở hộp 2: \(P(B|{A_2}) = 0\) (người dẫn chương trình không bao giờ mở hộp có quà)
- Khi quà ở hộp 3: \(P(B|{A_3}) = 1\) (người dẫn chương trình buộc phải mở hộp 2). Suy ra xác suất để người dẫn chương trình mở hộp 2 và quà ở trong hộp 3 là
\(P(B{A_3}) = P({A_3}).(B|{A_3}) = \frac{1}{3}.1 = \frac{1}{3}\)
b) Tính \(P(B)\) theo công thức xác suất toàn phần:
\(P(B) = P({A_1})P(B|{A_1}) + P({A_2})P(B|{A_2}) + P({A_3})P(B|{A_3})\)
\(P(B) = \frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times 0 + \frac{1}{3} \times 1 = \frac{1}{2}\)
* Tính \(P({A_1}|B)\):
\(P({A_1}|B) = \frac{{P({A_1}B)}}{{P(B)}} = \frac{{P({A_1})P(B|{A_1})}}{{P(B)}} = \frac{{\frac{1}{3} \times \frac{1}{2}}}{{\frac{1}{2}}} = \frac{1}{3}\)
* Tính \(P({A_3}|B)\):
\(P({A_3}|B) = \frac{{P({A_3}B)}}{{P(B)}} = \frac{{P({A_3})P(B|{A_3})}}{{P(B)}} = \frac{{\frac{1}{3} \times 1}}{{\frac{1}{2}}} = \frac{2}{3}\)
So sánh: \(P({A_3}|B) = \frac{2}{3} > P({A_1}|B) = \frac{1}{3}\)
Kết luận: Người chơi nên đổi sang hộp 3 vì xác suất quà ở hộp 3 (\(\frac{2}{3}\)) cao hơn xác suất quà ở hộp 1 (\(\frac{1}{3}\)).
- Khởi động
- LT1
- LT2
- LT3
- VD
Trả lời câu hỏi Khởi động trang 90 SGK Toán 12 Cùng khám phá
Một kho hàng chứa 80 sản phẩm cùng loại, bao gồm 30 sản phẩm do nhà máy I sản xuất (trong đó có 25 sản phẩm tốt, 5 sản phẩm kém chất lượng) và 50 sản phẩm do nhà máy II sản xuất (trong đó có 43 sản phẩm tốt, 7 sản phẩm kém chất lượng) như trong bảng (Bảng 6.1).

Lấy ngẫu nhiên một sản phẩm trong các sản phẩm này.
a) Gọi A là biến cố "Lấy được sản phẩm tốt" và B là biến cố "Lấy được sản phẩm do nhà máy I sản xuất". Tính \(P(B)\), \(P(AB)\).
b) Giả sử biến cố B đã xảy ra, tức là lấy được sản phẩm do nhà máy I sản xuất, tính xác suất để sản phẩm lấy được này là sản phẩm tốt.
c) Hãy so sánh kết quả của câu b với tỉ số \(\frac{{P(AB)}}{{P(B)}}\).
Phương pháp giải:
a) Tính xác suất theo công thức cổ điển: P(A) = số trường hợp thuận lợi / số trường hợp có thể.
b) Với xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\) .
c) So sánh các kết quả.
Lời giải chi tiết:
a) Tính \(P(B)\) và \(P(AB)\):
Theo đề bài ta có 30 sản phẩm do nhà máy I sản xuất trên tổng số 80 sản phẩm, suy ra xác suất lấy được sản phẩm do nhà máy I sản xuất là:
\(P(B) = \frac{{30}}{{80}} = 0,375\)
Trong 30 sản phẩm do nhà máy I sản xuất có 25 sản phẩm tốt, suy ra xác suất lấy được sản phẩm tốt do nhà máy I sản xuất là:
\(P(AB) = \frac{{25}}{{80}} = 0,3125\)
b) Tính xác suất có điều kiện:
- Khi biết sản phẩm do nhà máy I sản xuất, ta chỉ quan tâm đến 30 sản phẩm của nhà máy I
- Trong 30 sản phẩm của nhà máy I có 25 sản phẩm tốt
- \(P(A|B) = \frac{{25}}{{30}} = \frac{5}{6} \approx 0,8333\)
c) So sánh \(P(A|B)\) với \(\frac{{P(AB)}}{{P(B)}}\):
\(\frac{{P(AB)}}{{P(B)}} = \frac{{0,3125}}{{0,375}} = \frac{{25}}{{30}} = \frac{5}{6} \approx 0,8333\)
Kết luận: \(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{5}{6}\)
Trả lời câu hỏi Luyện tập 1 trang 92 SGK Toán 12 Cùng khám phá
Xét phép thử gieo một con xúc xắc cân đối đồng chất hai lần, quan sát số chấm xuất hiện trong mỗi lần gieo.
Tính xác suất để tổng số chấm trong hai lần gieo là 7, biết rằng lần gieo đầu tiên xuất hiện mặt 5 chấm.
Phương pháp giải:
Gọi A là biến cố "tổng số chấm là 7".
Gọi B là biến cố "lần gieo đầu xuất hiện 5 chấm".
Cần tính \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\).
Lời giải chi tiết:
* Xét không gian mẫu \(\Omega \):
- Mỗi lần gieo có 6 khả năng từ 1 đến 6 chấm
- Với 2 lần gieo độc lập, ta có \(|\Omega | = 6 \times 6 = 36\) phần tử
* Tính \(P(B)\):
- B là biến cố "lần gieo đầu xuất hiện 5 chấm"
- \(P(B) = \frac{1}{6}\) (vì xúc xắc cân đối)
* Tính \(P(AB)\):
- A là "tổng số chấm là 7"
- B là "lần đầu được 5 chấm"
- Do đã biết lần đầu được 5 chấm, muốn tổng là 7 thì lần 2 phải được 2 chấm. Gọi C là biến cố “lần hai được 2 chấm”
- \(P(AB) = P(B) \times P({\rm{C}}) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{{36}}\)
* Tính xác suất cần tìm \(P(A|B)\):
\(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}\)
Vậy xác suất để tổng số chấm trong hai lần gieo là 7, biết rằng lần gieo đầu tiên xuất hiện mặt 5 chấm là \(\frac{1}{6}\).
Trả lời câu hỏi Luyện tập 2 trang 93 SGK Toán 12 Cùng khám phá
Trở lại Hoạt động đầu bài, sử dụng Bảng 6.1, hãy tính xác suất để lấy được sản phẩm tốt, biết rằng sản phẩm lấy được do nhà máy II sản suất.
Phương pháp giải:
Gọi A là biến cố "lấy được sản phẩm tốt".
Gọi C là biến cố "lấy được sản phẩm do nhà máy II sản xuất".
Cần tính \(P(A|C) = \frac{{P(AC)}}{{P(C)}}\).
Lời giải chi tiết:
* Từ Bảng 6.1, ta có:
- Tổng số sản phẩm là 80
- Nhà máy II có 50 sản phẩm, trong đó:
+ 43 sản phẩm tốt
+ 7 sản phẩm kém chất lượng
- Gọi A là biến cố "lấy được sản phẩm tốt"
- Gọi C là biến cố "lấy được sản phẩm do nhà máy II sản xuất"
* Tính \(P(C)\):
- \(P(C) = \frac{{50}}{{80}} = \frac{5}{8} = 0,625\)
* Tính \(P(AC)\):
\(P(AC) = \frac{{43}}{{80}} = 0,5375\)
* Tính xác suất cần tìm \(P(A|C)\):
\(P(A|C) = \frac{{P(AC)}}{{P(C)}} = \frac{{\frac{{43}}{{80}}}}{{\frac{5}{8}}} = \frac{{43}}{{50}} = 0,86\)
Vậy xác suất để lấy được sản phẩm tốt, biết rằng sản phẩm đó do nhà máy II sản xuất là \(\frac{{43}}{{50}} = 0,86\) hay 86%.
Trả lời câu hỏi Luyện tập 3 trang 95 SGK Toán 12 Cùng khám phá
Công ty nước giải khát X tổ chức một chương trình khuyến mại như sau: Trong mỗi thùng 24 chai nước giải khát đều có hai chai trúng thưởng (giải thưởng được viết ở dưới nắp chai), người tham gia chương trình được mở nắp một cách ngẫu nhiên lần lượt hai chai trong một thùng. Tính xác suất để một người tham gia chương trình mở được cả hai chai đều trúng thưởng.

Phương pháp giải:
Sử dụng công thức xác suất của biến cố đồng thời.
Phân tích thành hai bước:
- Xác suất mở chai trúng thưởng đầu tiên.
- Xác suất mở chai trúng thưởng thứ hai (sau khi đã mở được chai trúng thưởng thứ nhất).
Lời giải chi tiết:
* Gọi các biến cố:
- \({A_1}\): chai mở đầu tiên trúng thưởng
- \({A_2}\): chai mở thứ hai trúng thưởng (sau khi chai đầu trúng thưởng)
- Cần tính \(P({A_1}{A_2})\)
Xác suất chai đầu tiên trúng thưởng:
\(P({A_1}) = \frac{2}{{24}} = \frac{1}{{12}}\)
- Xác suất chai thứ hai trúng thưởng khi chai đầu đã trúng:
\(P({A_2}|{A_1}) = \frac{1}{{23}}\)
(vì còn 1 chai trúng thưởng trong 23 chai còn lại)
\(P({A_1}{A_2}) = P({A_1}) \times P({A_2}|{A_1}) = \frac{1}{{12}} \times \frac{1}{{23}} = \frac{1}{{276}}\)
Vậy xác suất để một người tham gia chương trình mở được cả hai chai đều trúng thưởng là \(\frac{1}{{276}}\) (khoảng 0,36%).
Trả lời câu hỏi Vận dụng trang 95 SGK Toán 12 Cùng khám phá
Quay trở lại phần Khỏi động đầu bài, xét tình huống người chơi đã chọn hộp 1 và người dẫn chương trình đã cho mở hộp 2. Kí hiệu \({A_1}\), \({A_2}\), \({A_3}\) lần lượt là các biến cố "Quả có trong hộp 1", "Quả có trong hộp 2", "Quả có trong hộp 3" và B là biến cố "Người dẫn chương trình mở hộp 2".
a) Hoàn tất sơ đồ hình cây sau:
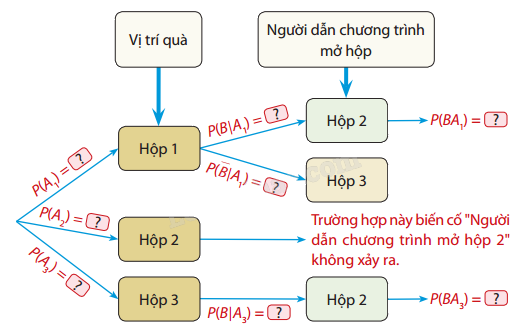
b) Tính \(P({A_1}|B)\) và \(P({A_3}|B)\). Từ đó cho biết người chơi nên giữ nguyên hộp mình đã lựa chọn ban đầu hay đổi số lựa chọn sang hộp khác thì cho khả năng lấy được quà cao hơn.
Phương pháp giải:
1. Xác định các xác suất từ sơ đồ hình cây
2. Sử dụng công thức xác suất có điều kiện: \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\)
3. Tính \(P(B)\) bằng công thức xác suất toàn phần
4. So sánh \(P({A_1}|B)\) và \(P({A_3}|B)\) để đưa ra kết luận
Lời giải chi tiết:
a) Từ sơ đồ hình cây, ta có:
- \(P({A_1}) = P({A_2}) = P({A_3}) = \frac{1}{3}\) (xác suất ban đầu quà ở mỗi hộp)
- Khi quà ở hộp 1: \(P(B|{A_1}) = \frac{1}{2}\) (người dẫn chương trình có thể chọn mở hộp 2 hoặc 3). Suy ra xác suất để người dẫn chương trình mở hộp 2 và quà ở trong hộp 1 là \(P(B{A_1}) = P({A_1}).(B|{A_1}) = \frac{1}{3}.\frac{1}{2} = \frac{1}{6}\)
- Khi quà ở hộp 2: \(P(B|{A_2}) = 0\) (người dẫn chương trình không bao giờ mở hộp có quà)
- Khi quà ở hộp 3: \(P(B|{A_3}) = 1\) (người dẫn chương trình buộc phải mở hộp 2). Suy ra xác suất để người dẫn chương trình mở hộp 2 và quà ở trong hộp 3 là
\(P(B{A_3}) = P({A_3}).(B|{A_3}) = \frac{1}{3}.1 = \frac{1}{3}\)
b) Tính \(P(B)\) theo công thức xác suất toàn phần:
\(P(B) = P({A_1})P(B|{A_1}) + P({A_2})P(B|{A_2}) + P({A_3})P(B|{A_3})\)
\(P(B) = \frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times 0 + \frac{1}{3} \times 1 = \frac{1}{2}\)
* Tính \(P({A_1}|B)\):
\(P({A_1}|B) = \frac{{P({A_1}B)}}{{P(B)}} = \frac{{P({A_1})P(B|{A_1})}}{{P(B)}} = \frac{{\frac{1}{3} \times \frac{1}{2}}}{{\frac{1}{2}}} = \frac{1}{3}\)
* Tính \(P({A_3}|B)\):
\(P({A_3}|B) = \frac{{P({A_3}B)}}{{P(B)}} = \frac{{P({A_3})P(B|{A_3})}}{{P(B)}} = \frac{{\frac{1}{3} \times 1}}{{\frac{1}{2}}} = \frac{2}{3}\)
So sánh: \(P({A_3}|B) = \frac{2}{3} > P({A_1}|B) = \frac{1}{3}\)
Kết luận: Người chơi nên đổi sang hộp 3 vì xác suất quà ở hộp 3 (\(\frac{2}{3}\)) cao hơn xác suất quà ở hộp 1 (\(\frac{1}{3}\)).
Giải mục 1 trang 90, 91, 92, 93, 94, 95 SGK Toán 12 tập 2: Tổng quan và hướng dẫn giải chi tiết
Mục 1 của SGK Toán 12 tập 2 thường tập trung vào việc củng cố và mở rộng kiến thức về đạo hàm, một trong những khái niệm quan trọng nhất trong chương trình Toán học lớp 12. Việc nắm vững kiến thức về đạo hàm không chỉ giúp các em giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng vững chắc cho các kỳ thi quan trọng như THPT Quốc gia.
Nội dung chính của Mục 1
- Đạo hàm của hàm số hợp: Ôn lại quy tắc tính đạo hàm của hàm hợp, một kỹ năng cần thiết để giải quyết nhiều bài toán phức tạp.
- Đạo hàm của hàm số lượng giác: Củng cố công thức tính đạo hàm của các hàm số lượng giác cơ bản (sin, cos, tan, cot).
- Ứng dụng đạo hàm để khảo sát hàm số: Tìm khoảng đồng biến, nghịch biến, cực trị, điểm uốn của hàm số.
- Bài toán thực tế liên quan đến đạo hàm: Giải các bài toán tối ưu hóa, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trong các tình huống thực tế.
Hướng dẫn giải chi tiết các bài tập trang 90, 91, 92, 93, 94, 95
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong Mục 1, trang 90, 91, 92, 93, 94, 95 SGK Toán 12 tập 2:
Bài 1 (Trang 90): Tính đạo hàm của các hàm số sau
Để giải bài này, các em cần áp dụng quy tắc tính đạo hàm của hàm hợp và đạo hàm của các hàm số cơ bản. Ví dụ, với hàm số y = sin(2x), đạo hàm của nó là y' = cos(2x) * 2 = 2cos(2x).
Bài 2 (Trang 91): Tìm đạo hàm cấp hai của hàm số
Để tìm đạo hàm cấp hai, các em cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một. Ví dụ, nếu y' = x^2 + 1, thì y'' = 2x.
Bài 3 (Trang 92): Khảo sát hàm số y = x^3 - 3x + 2
Để khảo sát hàm số, các em cần thực hiện các bước sau:
- Tìm tập xác định: Hàm số y = x^3 - 3x + 2 có tập xác định là R.
- Tính đạo hàm cấp một: y' = 3x^2 - 3.
- Tìm điểm dừng: Giải phương trình y' = 0 để tìm các điểm dừng. Trong trường hợp này, x = 1 và x = -1.
- Lập bảng biến thiên: Dựa vào dấu của đạo hàm cấp một để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận về cực trị: Dựa vào bảng biến thiên để xác định các điểm cực đại, cực tiểu của hàm số.
Bài 4, 5, 6... (Trang 93, 94, 95): Các bài tập ứng dụng khác
Các bài tập còn lại thường yêu cầu các em áp dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc tìm điều kiện để phương trình có nghiệm.
Lời khuyên khi giải bài tập
- Nắm vững lý thuyết: Hiểu rõ các công thức và quy tắc tính đạo hàm.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác.
- Sử dụng các công cụ hỗ trợ: Nếu cần thiết, hãy sử dụng máy tính hoặc các phần mềm toán học để kiểm tra kết quả.
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong Mục 1 trang 90, 91, 92, 93, 94, 95 SGK Toán 12 tập 2. Chúc các em học tập tốt!