Giải bài tập 3.10 trang 104 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 3.10 Trang 104 Toán 12 Tập 1
Bài tập 3.10 trang 104 SGK Toán 12 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ bản chất và phương pháp giải.
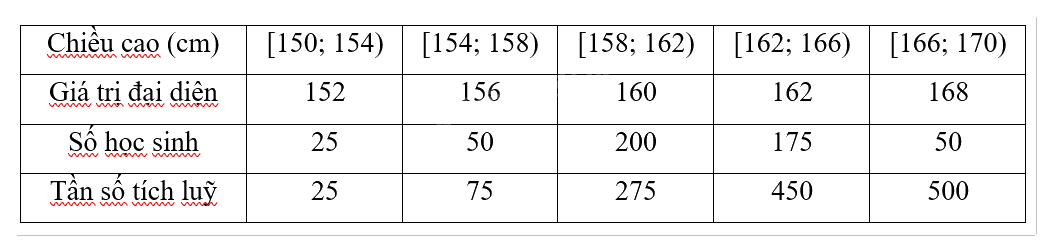
Chiều cao của 500 học sinh một trường trung học cơ sở được thống kê trong Bảng 3.25.
Đề bài
Chiều cao của 500 học sinh một trường trung học cơ sở được thống kê trong Bảng 3.25.

a) Tính khoảng tứ phân vị, trung bình và độ lệch chuẩn chiều cao của 500 học sinh.
b) Kết quả tìm được cho biết điều gì về chiều cao của 500 học sinh này?
Phương pháp giải - Xem chi tiết
a)
- Công thức tìm tứ phân vị: \({Q_x} = L + \left( {\frac{{{n_x} - F}}{f}} \right) \times h\)
- Khoảng tứ phân vị là khoảng giữa \({Q_3}\) và \({Q_1}\), ký hiệu là:\({\Delta _Q} = {Q_3} - {Q_1}\)
- Công thức tính trung bình là:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)
b)
Trung bình: Cho biết giá trị trung bình chiều cao của 500 học sinh. Nếu trung bình cao, có thể suy ra rằng chiều cao của nhóm này nói chung là cao.
Độ lệch chuẩn: Cho biết mức độ phân tán của các chiều cao xung quanh giá trị trung bình. Nếu độ lệch chuẩn lớn, điều đó có nghĩa là chiều cao của các học sinh rất khác nhau. Ngược lại, độ lệch chuẩn nhỏ cho thấy chiều cao của học sinh khá đồng đều.
Khoảng tứ phân vị: Giúp xác định sự phân tán của phần lớn dữ liệu (tức là 50% giữa). Nếu khoảng tứ phân vị nhỏ, điều đó cho thấy rằng phần lớn học sinh có chiều cao gần nhau. Nếu khoảng tứ phân vị lớn, điều đó chỉ ra rằng có sự khác biệt lớn về chiều cao giữa các học sinh.
Lời giải chi tiết
a)
Tứ phân vị:
- \(\frac{N}{4} = 125\) rơi vào nhóm [158; 162)
\({Q_1} = 158 + \frac{{125 - 75}}{{200}}.4 = 159\)
- \(\frac{{3N}}{4} = 375\) rơi vào nhóm [162; 166)
\({Q_3} = 162 + \frac{{375 - 275}}{{175}}.4 = 164,29\)
Khoảng tứ phân vị:
\({\Delta _Q} = {Q_3} - {Q_1} = 164,29 - 159 \approx 5,29\)
Chiều cao trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{n_i}} \right)} }}{N} = \frac{{152.25 + 156.50 + 160.200 + 164.175 + 168.50}}{{500}} = 161,4\)
Độ lệch chuẩn chiều cao của 500 học sinh:
- Tính \(\overline {{x^2}} \):
\(\overline {x_G^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{152}^2}.25 + {{156}^2}.50 + {{160}^2}.200 + {{164}^2}.175 + {{168}^2}.50}}{{500}} = 26064,8\)
- Tính độ lệch chuẩn
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {26064,8 - 161,{4^2}} \approx 3,85\)cm
b) Nhận xét về chiều cao của 500 học sinh:
Trung bình chiều cao là 161.4 cm, cho thấy chiều cao trung bình của nhóm học sinh này rơi vào khoảng giữa của dãy chiều cao đã cho.
Độ lệch chuẩn là 3.85 cm, điều này cho thấy có sự phân tán tương đối nhỏ về chiều cao giữa các học sinh. Phần lớn học sinh có chiều cao gần với giá trị trung bình.
Như vậy, các giá trị tứ phân vị cho thấy rằng 25% học sinh có chiều cao dưới 159 cm và 75% học sinh có chiều cao dưới 164.29 cm, với sự phân tán khoảng 5.29 cm giữa \({Q_1}\) và \({Q_3}\).
Giải Bài Tập 3.10 Trang 104 SGK Toán 12 Tập 1: Hướng Dẫn Chi Tiết
Bài tập 3.10 trang 104 SGK Toán 12 tập 1 thường thuộc chủ đề về đạo hàm của hàm số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
- Định nghĩa đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì.
- Các quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Đạo hàm của các hàm số cơ bản: Biết đạo hàm của các hàm số thường gặp như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit.
Nội Dung Bài Tập 3.10
Thông thường, bài tập 3.10 sẽ yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:
- Tính đạo hàm của một hàm số cho trước.
- Tìm đạo hàm của hàm số tại một điểm cụ thể.
- Xác định các điểm mà tại đó hàm số không có đạo hàm.
- Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến, vận tốc, gia tốc,...
Lời Giải Chi Tiết Bài Tập 3.10
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập 3.10 có nội dung như sau:
Cho hàm số f(x) = x3 - 3x2 + 2. Hãy tính f'(x) và tìm các điểm cực trị của hàm số.
Bước 1: Tính đạo hàm f'(x)
Sử dụng quy tắc tính đạo hàm của hàm đa thức, ta có:
f'(x) = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Bước 3: Xác định loại điểm cực trị
Ta xét dấu của f'(x) trên các khoảng:
- Khoảng (-∞; 0): f'(x) > 0 ⇒ Hàm số đồng biến
- Khoảng (0; 2): f'(x) < 0 ⇒ Hàm số nghịch biến
- Khoảng (2; +∞): f'(x) > 0 ⇒ Hàm số đồng biến
Vậy, hàm số có điểm cực đại tại x = 0 và điểm cực tiểu tại x = 2.
Mẹo Giải Bài Tập Đạo Hàm
Để giải các bài tập về đạo hàm một cách nhanh chóng và chính xác, các em có thể tham khảo một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản: Điều này giúp các em tiết kiệm thời gian và tránh sai sót.
- Sử dụng quy tắc chuỗi một cách linh hoạt: Quy tắc chuỗi là một công cụ mạnh mẽ để tính đạo hàm của các hàm hợp.
- Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả bằng cách lấy đạo hàm của đạo hàm để xem có trùng với hàm số ban đầu hay không.
Tổng Kết
Bài tập 3.10 trang 104 SGK Toán 12 tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại đặt câu hỏi trong phần bình luận bên dưới. Tusach.vn luôn sẵn sàng hỗ trợ các em!