Giải bài tập 2.23 trang 80 SGK Toán 12 tập 1 - Cùng khám phá
Tổng quan nội dung
Giải Bài Tập 2.23 Trang 80 SGK Toán 12 Tập 1
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 2.23 trang 80 SGK Toán 12 tập 1. Bài tập này thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
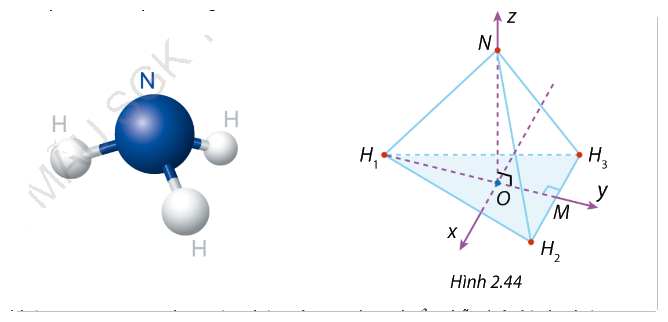
Trong Hoá học, cấu tạo của phân tử amoniac (\(N{H_3}\)) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (\(N\)) và đáy là tam giác \({H_1}{H_2}{H_3}\) với \({H_1}\), \({H_2}\), \({H_3}\) là vị trí của ba nguyên tử hydrogen (\(H\)). Góc tạo bởi liên kết \(H - N - H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1}\), \({H_2}\), \({H_3}\) (chẳng hạn như \({H_1}N{H_2}\)), được gọi là góc liên kết của phân tử \(N{H_3}\). Góc này xấp xỉ \({107^\circ }\). Trong khô
Đề bài
Trong Hoá học, cấu tạo của phân tử amoniac (\(N{H_3}\)) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (\(N\)) và đáy là tam giác \({H_1}{H_2}{H_3}\) với \({H_1}\), \({H_2}\), \({H_3}\) là vị trí của ba nguyên tử hydrogen (\(H\)). Góc tạo bởi liên kết \(H - N - H\), có hai cạnh là hai đoạn thẳng nối \(N\) với hai trong ba điểm \({H_1}\), \({H_2}\), \({H_3}\) (chẳng hạn như \({H_1}N{H_2}\)), được gọi là góc liên kết của phân tử \(N{H_3}\). Góc này xấp xỉ \({107^\circ }\).
Trong không gian Oxyz, cho một phân tử \(N{H_3}\) được biểu diễn bởi hình chóp tam giác đều \(N.{H_1}{H_2}{H_3}\) với \(O\) là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm \(N\) thuộc trục Oz, ba nguyên tử hydrogen ở các vị trí \({H_1}\), \({H_2}\), \({H_3}\) trong đó \({H_1}(0; - 2;0)\) và \({H_2}{H_3}\) song song với trục Ox (Hình 2.44).
a) Tính khoảng cách giữa hai nguyên tử hydrogen.
b) Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
a) Sử dụng định lý sin trong công thức để tính khoảng cách giữa hai nguyên tử hydrogen (d) có góc bằng ∝.
\(d = 2R.\sin (\alpha )\)
b) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian:
\(d(N,{H_1}) = \sqrt {{{({x_{{H_1}}} - {x_N})}^2} + {{({y_{{H_1}}} - {y_N})}^2} + {{({z_{{H_1}}} - {z_N})}^2}} \)
Thay các tọa độ tương ứng để tính khoảng cách \(d(N,{H_1})\), \(d(N,{H_2})\), \(d(N,{H_3})\).
Lời giải chi tiết
a)
Bởi vì tam giác \({H_1}{H_2}{H_3}\) là tam giác đều nên áp dụng vào định lý sin trong tam giác, ta có:
\({H_1}{H_2} = {H_1}{H_3} = {H_2}{H_3} = 2R\sin {60^\circ } = \sqrt 3 R\)
Trong trường hợp này, O là trọng tâm của tam giác \({H_1}{H_2}{H_3}\) và O cũng là bán kính đường tròn ngoại tiếp nên \(R = 2\), ta có: \(d = 2\sqrt 3 \)
b) Để tính khoảng cách giữa nguyên tử nitrogen \(N(0;0;z)\) với nguyên tử hydrogen \({H_1}(0; - 2;0)\), ta sử dụng công thức:
\(N{H_1} = \sqrt {{{(0 - 0)}^2} + {{(0 + 2)}^2} + {{(z - 0)}^2}} = \sqrt {4 + {z^2}} \)
Vì khoảng cách từ gốc toạ độ O đến \({H_2}\) là 2, do đó \({H_2}\) có toạ độ là
\({H_2}(2\cos \theta ;2\sin \theta ;0)\)
Với θ là góc \(\widehat {xO{H_2}}\). Và vì \({H_1}{H_2}{H_3}\) là tam giác đều nên \(\widehat {xO{H_2}} = 30^\circ \).
Vậy \({H_2}\) có toạ độ là: \({H_2}(\sqrt 3 ;1;0)\)
Toạ độ của vectơ \(\overrightarrow {N{H_1}} ,\overrightarrow {N{H_2}} \)là:
\(\overrightarrow {N{H_1}} = \left( {0; - 2; - z} \right),\overrightarrow {N{H_2}} = \left( {\sqrt 3 ;1; - z} \right)\)
Từ đó ta có \(z\): \(\cos {107^\circ } = \frac{{\overrightarrow {N{H_1}} .\overrightarrow {N{H_2}} }}{{\left| {\overrightarrow {N{H_1}} } \right|.\left| {\overrightarrow {N{H_2}} } \right|}} = \frac{{ - 2 + {z^2}}}{{4 + {z^2}}}\)
Suy ra: \( - 2 + {z^2} = \left( {4 + {z^2}} \right).\cos 107^\circ \Leftrightarrow 0,71{z^2} = 0,83 \Rightarrow z = 1,08\).
Giải Bài Tập 2.23 Trang 80 SGK Toán 12 Tập 1: Chi Tiết và Dễ Hiểu
Bài tập 2.23 trang 80 SGK Toán 12 tập 1 yêu cầu chúng ta khảo sát hàm số và tìm cực trị. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
- Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
- Tính đạo hàm cấp một (f'(x)): Đây là bước quan trọng để tìm các điểm cực trị.
- Tìm các điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị.
- Xác định loại cực trị: Sử dụng dấu của đạo hàm cấp hai (f''(x)) hoặc xét dấu của f'(x) xung quanh các điểm nghi ngờ để xác định xem đó là cực đại, cực tiểu hay điểm uốn.
- Lập bảng biến thiên: Dựa vào các điểm cực trị và khoảng biến thiên của hàm số để vẽ bảng biến thiên.
Phân Tích Chi Tiết Bài Tập 2.23
Giả sử hàm số cần khảo sát là y = f(x) = x3 - 3x2 + 2 (ví dụ minh họa). Chúng ta sẽ áp dụng các bước trên để giải bài tập này:
- Tập xác định: Hàm số xác định trên R.
- Đạo hàm cấp một: f'(x) = 3x2 - 6x
- Tìm điểm cực trị: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Xác định loại cực trị:
- f''(x) = 6x - 6
- f''(0) = -6 < 0 => x = 0 là điểm cực đại.
- f''(2) = 6 > 0 => x = 2 là điểm cực tiểu.
- Lập bảng biến thiên:
x -∞ 0 2 +∞ f'(x) + 0 - + f(x) ↗ 2 -2 ↗
Mẹo Giải Bài Tập Khảo Sát Hàm Số
Để giải các bài tập khảo sát hàm số một cách nhanh chóng và chính xác, các em có thể tham khảo một số mẹo sau:
- Nắm vững các công thức đạo hàm cơ bản: Điều này giúp các em tính đạo hàm một cách nhanh chóng và tránh sai sót.
- Sử dụng các phương pháp xét dấu đạo hàm: Phương pháp này giúp các em xác định khoảng đồng biến, nghịch biến và cực trị của hàm số.
- Vẽ bảng biến thiên: Bảng biến thiên giúp các em hình dung rõ hơn về sự biến thiên của hàm số.
- Luyện tập thường xuyên: Luyện tập là cách tốt nhất để nắm vững kiến thức và kỹ năng giải bài tập.
Tusach.vn – Đồng Hành Cùng Các Em
Tusach.vn luôn cập nhật những lời giải bài tập Toán 12 mới nhất và chi tiết nhất. Chúng tôi hy vọng rằng với những hướng dẫn trên, các em sẽ tự tin giải quyết bài tập 2.23 trang 80 SGK Toán 12 tập 1 và đạt kết quả tốt trong môn Toán. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ!